2.7 Мода оптического излучения

Вышесказанное в разделах 1 и 2 позволяет ввести понятие моды оптического излучения в следующем виде.

Мода оптического излучения представляет собой электромагнитную волну, характеризующуюся:

1. частотой излучения;

2. временной и пространственной когерентностью;

3. поляризацией вектора (TE или TM мода);

4. дискретным углом падения на границу разделаn_С ® n₀;

5. модовым квантовым числом (m);

6. эффективным волноводным показателем преломления ;

7. постоянной распространения , где– модуль волнового вектора в вакууме.

2.8 Конструкция цилиндрического диэлектрического волновода – стекловолокна (св)

Конструкция СВ показана на рисунке 2.12. Такое СВ имеет ступенчатый профиль распределения АПП вдоль диаметра СВ. Для обеспечения условия ПВО, АПП центральной части СВ, (n_С), незначительно превышает АПП оболочки n₀. Например, n_С = 1,48; n₀ = 1,46.

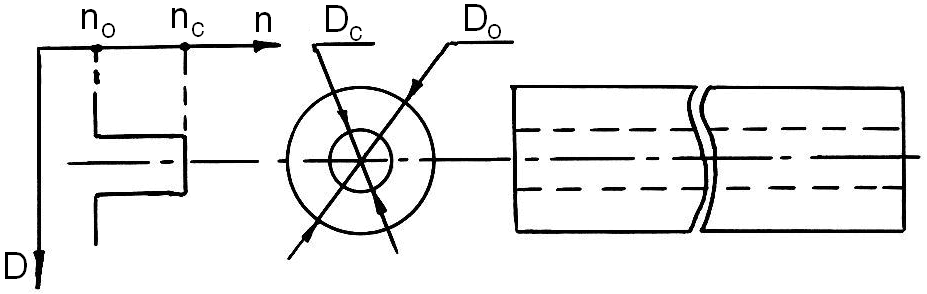
Рисунок 2.12 – Цилиндрический волновод

Типичные размеры диаметров центральной части волокна D_C и оболочки D₀ следующие: D_C = 50мкм, D₀ = 120мкм. Для повышения механической прочности на, СВ наносится полимерное покрытие, которое на рисунке 2.12 не показано.

2.9 Номинальная числовая апертура стекловолокна

Направим световой пучок на торец СВ так, как показано на рисунке 2.13. Пучок ограничен двумя крайними лучами 1 и 2. Луч 1 составляет угол g_К с осью симметрии СВ, луч 2 распространяется вдоль оси симметрии СВ.

Луч 1 преломляется на границе n_V ® n_С под углом b и превращается в луч 3. Соответствующая лучу 3 волна в точке B распадается на две, волна 4 преломляется в среду с АПП = n₀ под углом a, волна 5 отражается от границы n_С ® n₀.

Рисунок 2.13

Назовем угол g_К – критическим и потребуем, чтобы ему соответствовал предельный угол падения j = j_ПР на границу раздела n_С ® n₀, как показано на рисунке 2.13. Тогда угол преломления и волна 4 скользит вдоль границы разделаn_С ® n₀. В окрестности точки A закон преломления света имеет вид: , где– АПП среды, из которой свет попадает на торецCB. Из треугольника ABC следует ;. Следовательно:

, (2.12)

В окрестности точки B:

, (2.13)

Возводя во вторую степень (2.12) и (2.13) складывая их почленно, имеем:

,

(2.14)

Выражение (2.14) носит название нормальной числовой апертуры стекловолокна. Согласно рисунков 2.13 и 2.14, при g < g_К в окрестности точки B имеет место ПВО, и свет распространяется вдоль СВ по зигзагообразной траектории. При g > g_К условие ПВО не выполняется, и энергия волны 3 постепенно переводится в оболочку.

Рисунок 2.14

2.10 Квантование углов j и g в стекловолокне

Если световой пучок распространяется зигзагообразно по СВ в плоскости, проходящей чрез ось симметрии СВ, рисунок 2.13, и выполняется условие ПВО, для СВ, как и для планарного волновода, имеет место поперечный резонанс в виде, аналогичный формуле (2.11)

(2.15)

где D_C - диаметр центральной части СВ. Согласно (2.15), угол =квантован, а

(2.16)

По аналогии с (2.12),

(2.17)

Из (2.16) и (2.17) следует, что

(2.18)

Согласно (2.16) и (2.18), квантованные углы иимеют значения:

(2.19)

(2.20)

где m = 0, 1, 2, 3……