
- •1)Векторный
- •2)Координатный –задаётся зависимостью координат от времени
- •3)Естественный (траекторный)
- •6) Связь между линейными и угловыми величинами, характеризующими двидение
- •7. Инерциальные системы отсчёта, первый закон Ньютона
- •8. Второй закон Ньютона. Импульс материальной точки и системы материальных точек. Третий закон Ньютона
- •9. Закон сохранения импульса
- •10)Центр масс и закон его движения.
- •11)Энергия, работа, мощность.
- •12)Кинетическая и потенциальная энергии. Полная механическая энергия.
- •13. Понятие о градиенте скалярной функции. Связь силы и потенциальной энергии.
- •14.Закон сохранения механической энергии. Консервативные и неконсервативные силы.
- •15. Применений законов сохранения энергии и импульса к собственному удару двух тел.
- •16. Применение законов сохранения энергии и импульса к абсолютно неупругому центральному удару двух тел.
- •17. Вращательное движение твёрдого тела. Момент инерции тела относительно оси. Теорема Штейнера.
- •18. Вывод формулы момента инерции однородного цилиндра.
- •19)Кинетическая энергия вращательного и плоского движения.
- •20)Момент силы относительно точки и оси. Работа при вращательном движении. Основное уравнение динамики вращательного движения.
- •22) Сравнение характеристик поступательного и вращательного движения.
- •23)Гармонические колебания и их характеристика. Диф. Уравнение гармонических колебаний. Квазиупругие силы. Метод векторных диаграмм.
- •24) Пружинный, физический и математический маятники. Вывод формулы периода их колебаний. Приведенная длинна физического маятника.
- •25. Степени гармонических колебаний одного направления и одинаковой частоты
- •26. Механические волны. Продольные и поперечные волны. Уравнение бегущей волны. Длина волны. Волновое число. Фазовая скорость.
- •27.Идеальный газ. Опытные законы идеального газа(изопроцессы) уравнение Клайперона- Менделеева.
- •Вопрос 28. Число степеней свободных молекул. Закон равномерного распределения по степеням свободы молекул. Внутренняя энергия идеального газа.
- •Вопрос 29. Первое начало термодинамики. Работа газа при изменении его объема.
- •Вопрос 30. Применение первого начала термодинамики к изопроцессам.
- •31.Виды теплоёмкостей. Молярная теплоёмкость при постоянном объёме и давлении. Уравнение Майнера.
- •32.Адиабатический процесс. Уравнение Пуассона. Показатель адиабаты.
- •33) Обратимые и необратимые процессы. Кпд тепловой машины. Цикл Карно.
- •34. Электрический заряд. Закон сохранения заряда. Электростатическое поле. Закон Кулона.
- •35. Напряжённость электрического поля. Поток вектора напряжённости. Силовые линии электрического поля. Принцип суперпозиции электрических полей.
- •36. Теорема Остроградского-Гаусса для электростатического поля в вакууме. Применение теоремы к расчёту полей (а,б).
- •37. Работа электростатического поля при перемещении в нем заряда. Потенциал электростатического поля. Циркуляция вектора напряженности электростатического поля.
- •Вопрос 38. Связь напряженности и потенциала электростатического поля. Эквипотенциальные поверхности
- •40) Электрическое смещение. Теорема Остроградского Гаусса для электростатического поля в диэлектрике.
- •41) Электроемкость уединенного проводника и конденсатора. Типы конденсаторов. Электроемкость плоского конденсатора, соединение конденсаторов.
- •42) Энергия системы неподвижных точечных зарядов. Заряженного проводника, конденсатора.
- •43. Энергия электростатического поля. Объемная плотность энергии.
- •44. Условие существование электрического тока. Сила и плотность тока.
- •45. Сторонние силы. Электродвижущая сила и напряжение
- •47)Работа и мощность тока. Закон Джоуля-Ленца
- •52.Циркуляция вектора индукции магнитного поля. Теорема о циркуляции вектора индукции магнитного поля в вакууме(закон полного тока). Применение закона полного тока к расчёту поля соленоида .
- •53.Поток вектора магнитной индукции. Теорема Остроградского-Гаусса для магнитного поля. Потокосцепление. Работа по перемещению проводника и контура с током в магнитном поле.
- •54.Явление электромагнитной индукции. Закон Фарадея. Правило Ленца.
- •55)Явление само- и взаимоиндукции. Индуктивность.
- •56)Энергия магнитного поля. Объемная плотность энергии магнитного поля.
- •57) Электромагнитные волны. Уравнение плоской монохроматической э/м волны. Свойства э/м волн, энергия переносимая волной.
7. Инерциальные системы отсчёта, первый закон Ньютона
Инерциальная система отсчёта – система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно, либо покоятся.
Первый закон Ньютона: существуют такие системы отсчета, в которых тело движется прямолинейно и равномерно или находится в состоянии покоя в том случае, если на тело не действуют силы или все силы, действующие на тело, скомпенсированы.
Инерциальной системой отсчета называется такая система, в которой выполняются законы Ньютона.
8. Второй закон Ньютона. Импульс материальной точки и системы материальных точек. Третий закон Ньютона
Второй закон Ньютона: ускорение, которое получает тело, прямо пропорционально приложенной к телу силе и обратно пропорционально массе тела.
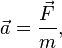 а-ускорение
тела, F
– сила, приложенная к телу, m
– масса тела
а-ускорение
тела, F
– сила, приложенная к телу, m
– масса тела
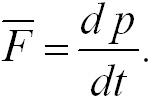 p-импульс
тела
p-импульс
тела
Импульс p материальной точки определен как p mv
Импульс системы материальных точек p=m1v1+m2v2+m3v3+…
Третий закон Ньютона: Каждой силе F соответствует сила противодействия F’(сила реакции), равная по величине, но противоположно направленная
![]()
Силы, действующие между частями одного и того же тела, называются внутренними. Если тело движется как целое, то его ускорение определяется только внешней силой. Внутренние силы исключаются из второго закона Ньютона, так как их векторная сумма равна нулю.
9. Закон сохранения импульса
замкнутой изолированной системой называют такую, в которой тела взаимодействуют только друг с другом и не взаимодействуют с внешними телами.
Для замкнутой системы справедлив закон сохранения импульса: в замкнутой системе импульс всех тел остается величиной постоянной.
Обратимся
к тому, как записывается
закон сохранения импульса
для системы из двух тел: ![]() .
.
Эту
же формулу мы можем записать
следующим образом: 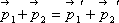 .
.
10)Центр масс и закон его движения.
Рассмотрим
систему материальных точек(с.м.т.) с
массами m(1),m(2)…m(n)
,положение которых в пространстве
соответственно определяется
радиус-векторами
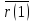 ,
, …
… Центрами
масс с.м.т. называют воображаемую точку,
положение которой выражается уравнением:
Центрами
масс с.м.т. называют воображаемую точку,
положение которой выражается уравнением: =
=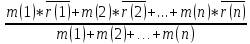 (1)
(1)
Пусть
М=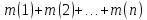 −суммарная
масса с.м.т. ,тогда (1) запишем в виде:
−суммарная
масса с.м.т. ,тогда (1) запишем в виде:
M*r(c)=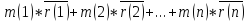
Возьмём производную по времени от обоих частей этого уравнения.
M*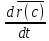 =m(1)
=m(1) +m(2)
+m(2)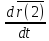 +…+
+…+ ;
;

Учитывая определение скорости, последнее выражение примет вид:
М*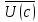 =m(1)*
=m(1)*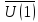 +m(2)*
+m(2)*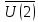 +…+m(n)*
+…+m(n)* (2)
(2)
 М*
М*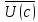 −импульс
центра масс. В первой части формулы
(2)−импульс с.м.т.
−импульс
центра масс. В первой части формулы
(2)−импульс с.м.т. (3)
(3)
Согласно
формуле
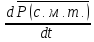 =
=
 таким
образом ,используя формулу (3) можно
записать
таким
образом ,используя формулу (3) можно
записать =
=
 ,т.е.
,т.е. =
=
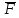 или
или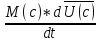 =
=
 ,
где
,
где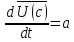 −ускорение.
−ускорение.
Закон
движения центра масс М* =
= (4)
(4)
Если
система замкнута, то
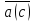 =0
и
=0
и
 =0,т.е.
в этом случае центр масс либо покоится,
либо движется равномерно прямолинейно
.
=0,т.е.
в этом случае центр масс либо покоится,
либо движется равномерно прямолинейно
.
