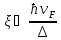Теоретическое объяснение эффекта сверхпроводимости.

Уравнения Лондонов.

Первая попытка построить макроскопическую теорию сверхпроводников, точнее их электродинамику была осуществлена в 1935 году братьями Ф. Лондоном и Г. Лондоном. Они хотели, не вдаваясь в микроскопические причины сверхпроводимости, невыясненные к тому времени, записать в математической форме основные экспериментальные факты: отсутствие сопротивления и эффект Мейсснера. Они резонно предположили, что носителями тока в сверхпроводнике, так же как в металле, являются электроны проводимости. Равенство нулю сопротивления (ρ = 0) означает что электрон при своем движении не испытывает столкновений, т. е. свободно ускоряется под действием электрического поля E.

где j – плотность тока, 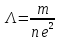– постоянная, n – концентрация электронов.

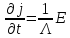
Эти два уравнения и представляет собой основу Лондоновской электродинамики сверхпроводников.

Глубина проникновения магнитного поля в сверхпроводник

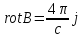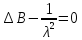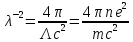При помощи уравнения Максвелла запишем , где или .

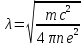Величина λ называется лондонской длиной проникновения.

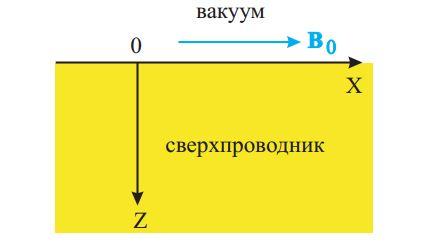
Рассмотрим случай, когда сверхпроводник занимает полупространство z > 0 — рис.6 . И пусть x компонента магнитного поля снаружи сверхпроводника равна

Рис. 6: Полупространство занятое сверхпроводником в магнитном поле.

Тогда 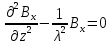имеем решение 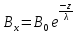, т.е. магнитное поле экспоненциально спадает вглубь сверхпроводника на длине λ.

Давайте оценим теперь глубину проникновения магнитного поля в сверхпроводник. Согласно полученной нами формуле

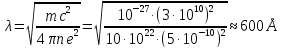
Таким образом, магнитное поле в сверхпроводник все же проникает, но на небольшую глубину, порядка 500 − 1000 Å.

Рис. 7: Зависимость глубины проникновения от температуры.

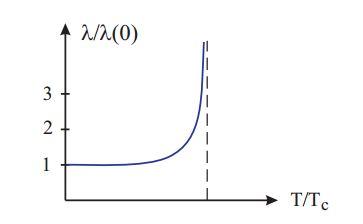
Глубина проникновения не является постоянной величиной и изменяется с изменением температуры — рис. 7. Эта зависимость имеет вид

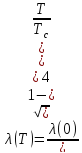
В точке сверхпроводящего перехода λ обращается в бесконечность.

Куперовские пары. Длина когерентности.

Для описания сверхпроводников даже на макроскопическом уровне необходимо применение квантовой механики. Дело в том, что сверхпроводимость — явление сугубо квантовое. Объяснить ее с классических позиций невозможно. В сверхпроводнике, так же как и в металле, в переносе тока участвуют электроны проводимости. Однако, существенное различие между теми и другими заключается в том, что если в металле электроны движутся нескоррелированно под действием приложенного электрического поля (каждый сам по себе), то в сверхпроводнике возникает корреляция в движении электронов. Пространственный масштаб, на котором электроны сверхпроводника ”чувствуют” друг друга, называется длина когерентности ξ. Физической причиной возникновения корреляции в движении электронов является существующее в сверхпроводнике эффективное притяжение между ними. Это притяжение как бы объединяет электроны с противоположно направленными спинами в пары, называемые куперовскими парами — рис. 8.

Рис. 3: Куперовские пары в сверхпроводнике.

Характерный размер такой пары и является длиной когерентности ξ. В чистых металлах величина ξ ' 10−4 см = 10000 Å. Возникает естественный вопрос: как такие пары могут помещаться в металле не мешая друг другу. Ведь из оценок лондоновской длины проникновения следует, что концентрация электронов в металле, принимающих участие в сверхпроводимости, порядка 1022 — 1023 см−3 . Это значит, что пары ”проникают” друг через друга и в то же время как частицы газа являются свободными и практически не взаимодействуют друг с другом. Такое положение возможно только в квантовой механике, так же как течение этого ”газа” куперовских пар через решетку без рассеяния.

В чем же причина притяжения между электронами в сверхпроводнике. Ведь электроны, являясь отрицательно заряженными частицами, по закону Кулона должны отталкиваться друг от друга. Такое кулоновское отталкивание действительно имеет место в вакууме. Но в сверхпроводнике (в металле) электроны движутся не в вакууме, а в кристаллической решетке. Естественно, что при своем движении они деформируют решетку. Деформация решетки позволяет им понизить потенциальную энергию, поэтому естественно, что электроны будут притягиваться к месту деформации.

Такой механизм сверхпроводимости называется фононным и был введен в работе Бардина, Купера и Шрифера (БКШ в 1956 г.) и одновременно Боголюбовым 6 в 1958 г. Фононным же этот механизм называется потому, что два электрона, пролетая друг мимо друга, обмениваются виртуальным фононом (квантом колебаний кристаллической решетки) с энергией ħω и импульсом ħk — рис. 9.

Рис. 5: Взаимодействие двух электронов за счет обмена виртуальным фононом.

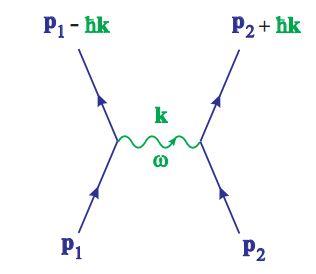
Таким образом, образование куперовских пар или куперовское спаривание электронов в сверхпроводнике выгодно с энергетической точки зрения (это понижает энергию системы). Существенно, что при спаривании образуется частица, называемая куперовской парой, со спином 0.

Поскольку образование куперовских пар энергетически выгодно, то, чтобы разорвать такую пару, необходимо затратить энергию, которую обозначим через ∆. Очевидно, что когда тепловая энергия kT сравняется с ∆, куперовская пара разрушится и сверхпроводимость исчезнет. Поэтому,

Если теперь ввести в рассмотрение скорость электронов в металле —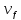(скорость электронов, обладающих энергией Ферми), то длину когерент- ности можно выразить через них следующим образом