Калинин / Приборостроителям / Математика 1 (11)
.doc
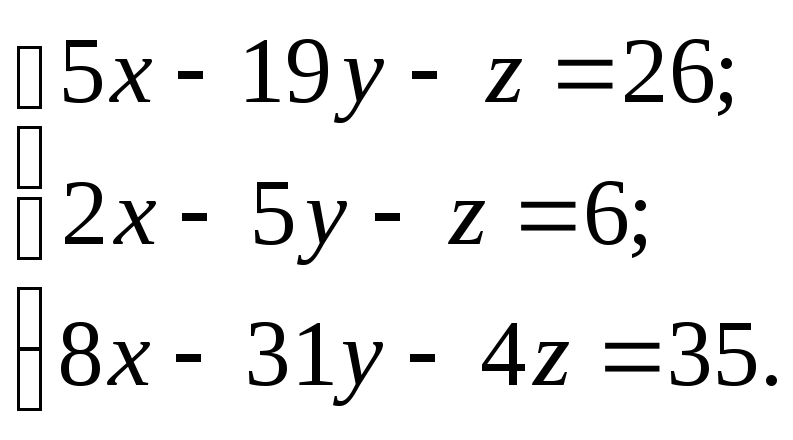 Решить
систему линейных алгебраических
уравнений методами 1) Крамера; 2) обратной
матрицы; 3)Гаусса.
Решить
систему линейных алгебраических
уравнений методами 1) Крамера; 2) обратной
матрицы; 3)Гаусса.
-
Метод Крамера
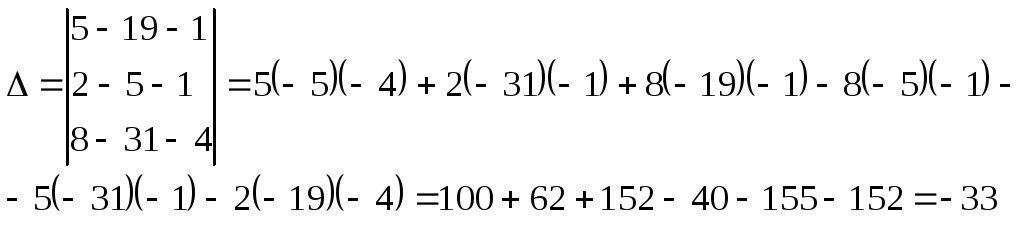
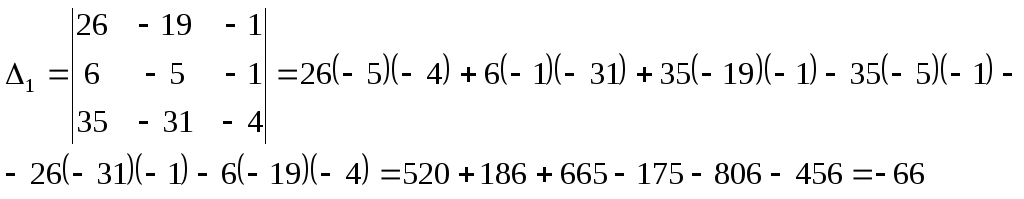
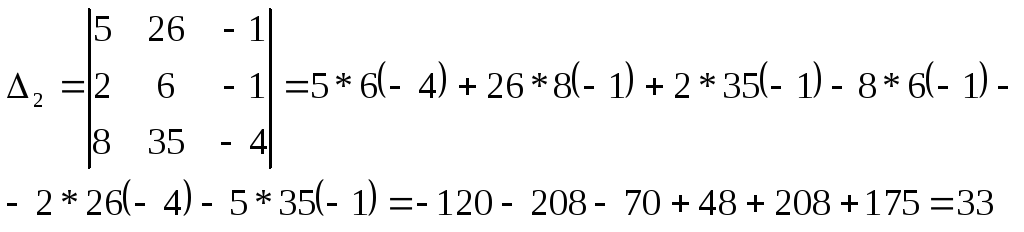
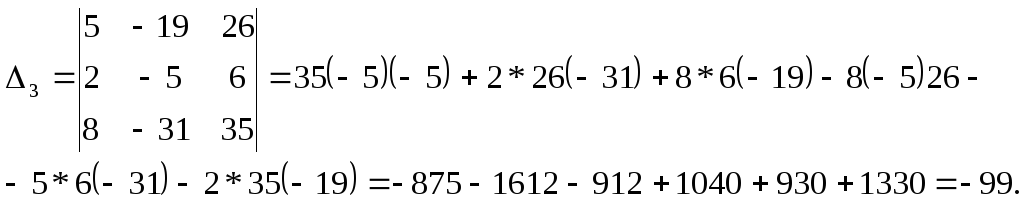
Отсюда
![]() ;
;
![]() ;
;
![]() .
.
Проверка:
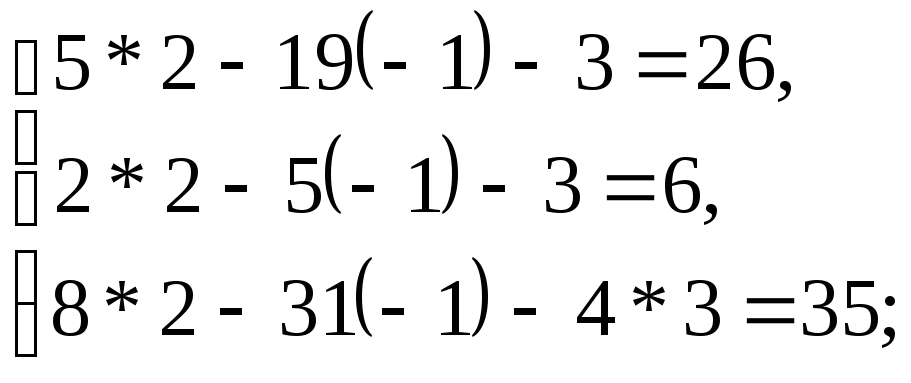
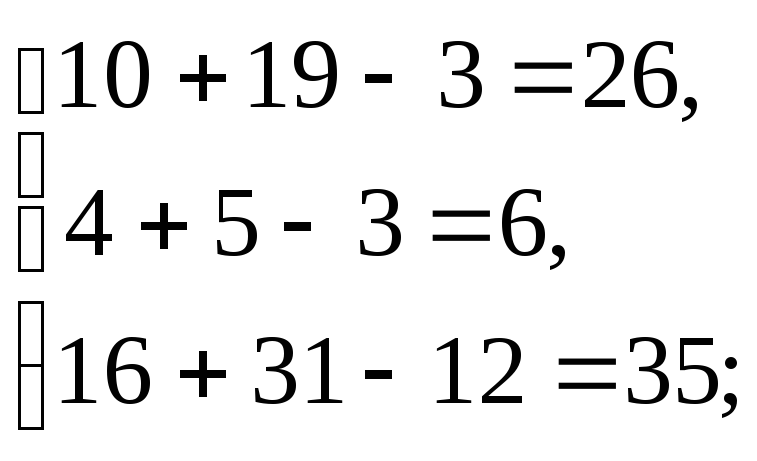
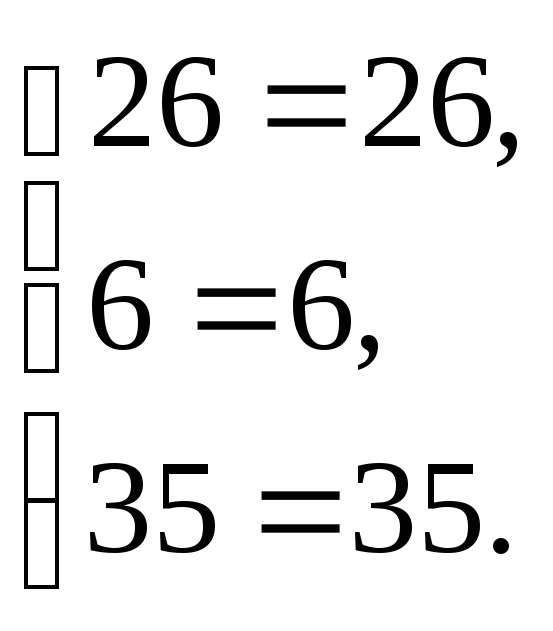
Уравнения системы превратились в верные тождества, что подтверждает правильность решения.
-
Метод обратной матрицы.
Главный определитель определили в предыдущем методе:
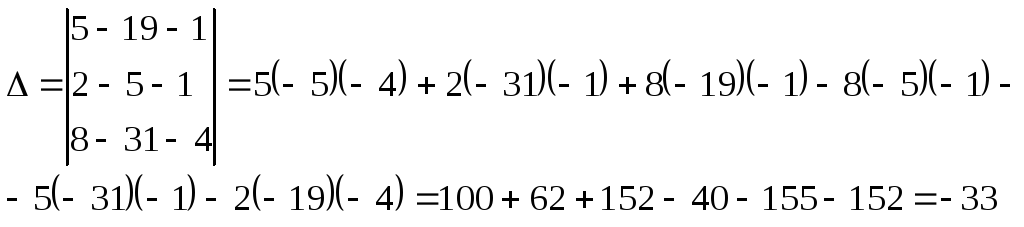
Вычислим алгебраические дополнения элементов этого определителя:
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Тогда обратная матрица имеет вид

Следовательно

Следовательно:
![]() ;
;
![]() ;
;
![]() .
– что совпадает с предыдущим методом.
.
– что совпадает с предыдущим методом.
-
Метод Гаусса.
Составим расширенную матрицу системы
и поменяем местами первую и вторую
строки. Затем вычтем из второй строки
первую, умноженную на
![]() ,
а из третьей первую, умноженную на 4.
,
а из третьей первую, умноженную на 4.
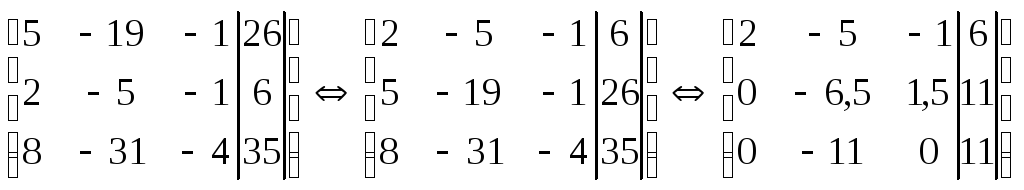
Система уравнений приняла треугольный вид:
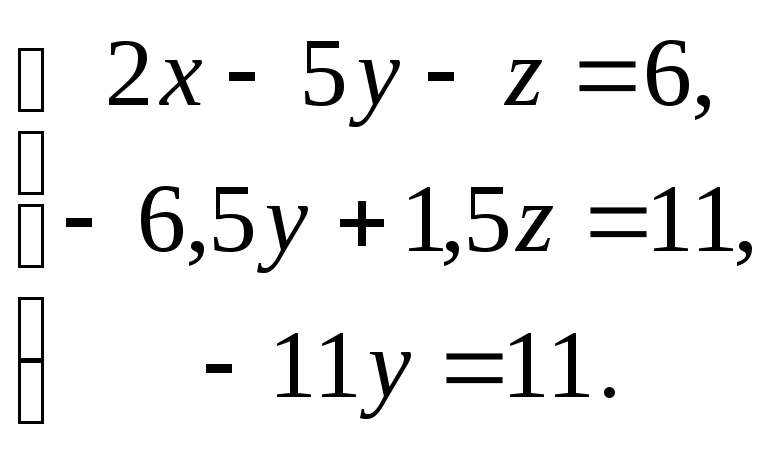 Из последнего уравнения имеем
Из последнего уравнения имеем
![]() .
.
Подставляя это значение во второе
уравнение получаем
![]() .
.
Теперь из первого уравнения находим х.
![]() .
.
![]() ;
;
![]() ;
;
![]() .
.
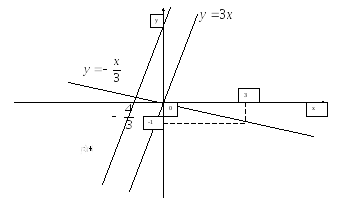
Задача 11.
;![]()
![]() .
.
Преобразуем заданное уравнение
![]() .
.
Отсюда угловой коэффициент прямой
равен:
![]()
![]()
Задавая
![]() ,
получим
,
получим
![]() ;
Задавая
;
Задавая
![]() ,
получим
,
получим
![]() .
.
Параллельные прямые имеют одинаковый угловой коэффициент.
Например:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Производные угловых коэффициентов
перпендикулярных прямых равно -1. Поэтому
угловой коэффициент прямых, перпендикулярных
заданной прямой, будет равен
![]() .
Если прямая проходит через начало
координат, то свободный член в уравнении
такой прямой равен 0.
.
Если прямая проходит через начало
координат, то свободный член в уравнении
такой прямой равен 0.
Тогда уравнение прямой, перпендикулярной
к данной и проходящей через начало
координат, будет иметь вид:
![]() .
.
35) а)
![]() - находим как производную от произведения
функций:
- находим как производную от произведения
функций:
![]()
![]() .
.
б)
![]() -
находим как производную от сложной
функции.
-
находим как производную от сложной
функции.
![]() .
.
44) 1) Область определения:
![]() .
.
2)
![]() - функция четная.
- функция четная.
3)
![]() - (0;3) – точка пересечения с осью y.
- (0;3) – точка пересечения с осью y.
![]() ,
пересечений с осью х нет.
,
пересечений с осью х нет.
-
Функция больше нуля на всей области определения.
Экстремумы:
![]()
Точки экстремума:
![]()
![]() - функция убывает.
- функция убывает.
![]() -
функция возрастает.
-
функция возрастает.
Значит точка х=0 – максимум; х=-1 и х=1 – точки минимума.
-
Точки перегиба:
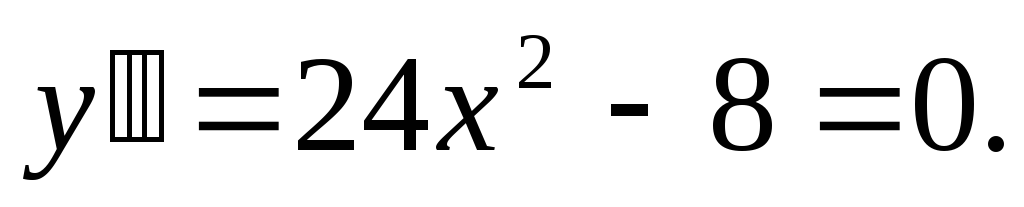
 .
.
Интервал выпуклости
![]() .
.
Интервал вогнутости
![]() .
.
6)
![]() - асимптот нет.
- асимптот нет.