Калинин / Приборостроителям / Математика 1 (18)
.docКонтрольная работа №1
-
По формулам Крамера решить систему линейных уравнений:
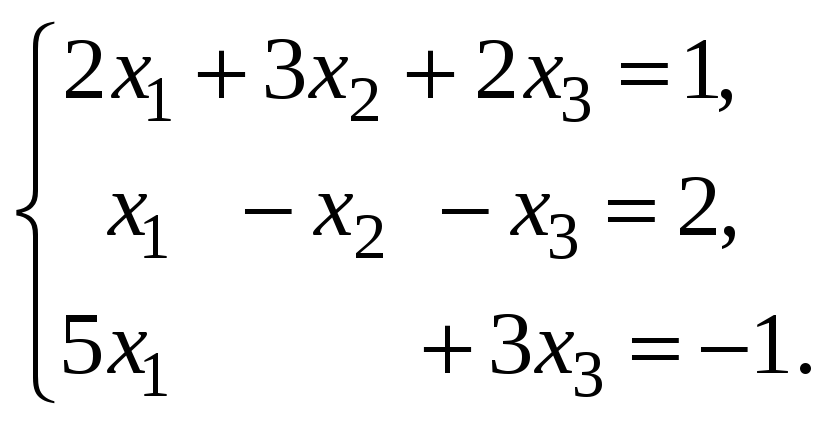
Решение
Найдём главный определитель системы:
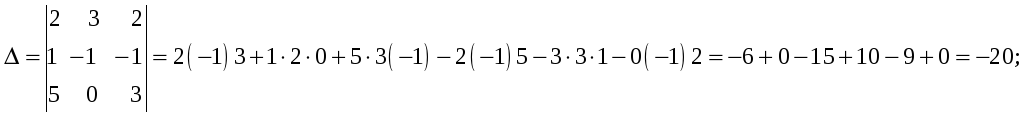
Найдём вспомогательные определители данной системы:
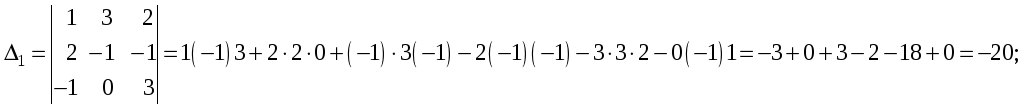
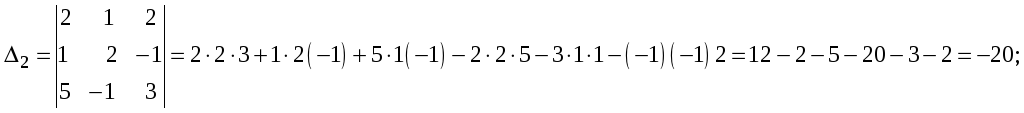

По формулам Крамера определим
![]()
-
Найти предел:
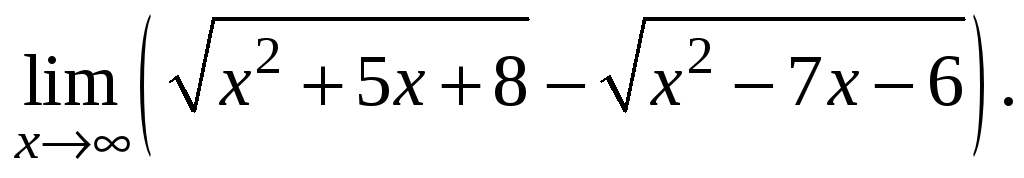
Решение
![]() Для того, чтобы избавиться от
неопределённости, домножим числитель
и знаменатель на выражение сопряжённое
данному
Для того, чтобы избавиться от
неопределённости, домножим числитель
и знаменатель на выражение сопряжённое
данному
![]() ,
получаем:
,
получаем:
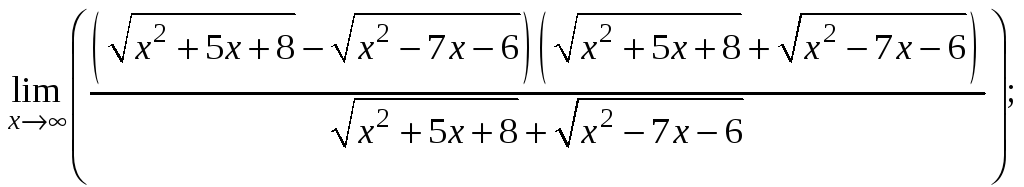
Преобразуем и воспользуемся для раскрытия
неопределённости вида
![]() правилом Лопиталя, дифференцируя по
отдельности числитель и знаменатель:
правилом Лопиталя, дифференцируя по
отдельности числитель и знаменатель:
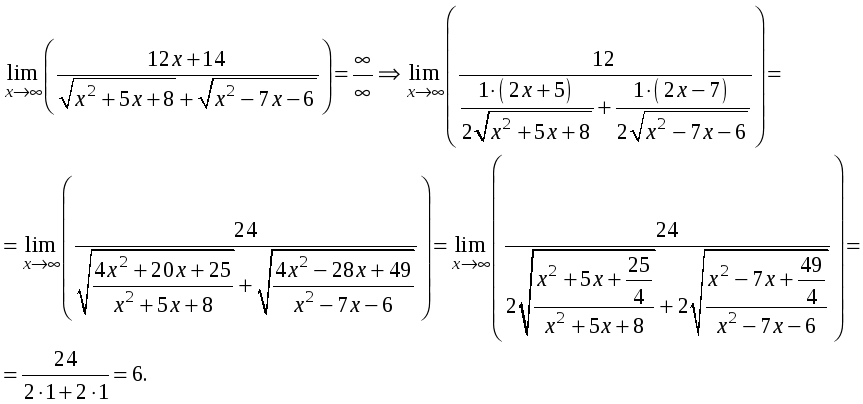
Так как полученные подкоренные выражения стремятся к единице при стремлении аргумента к бесконечности.
-
Найти производную функции:
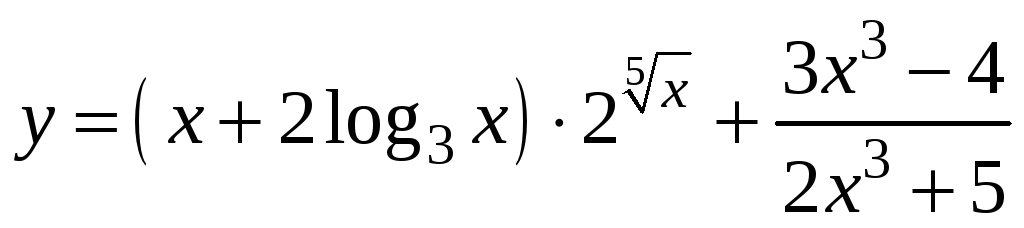 .
.
Решение
Дифференцируем как сумму сложных функций:
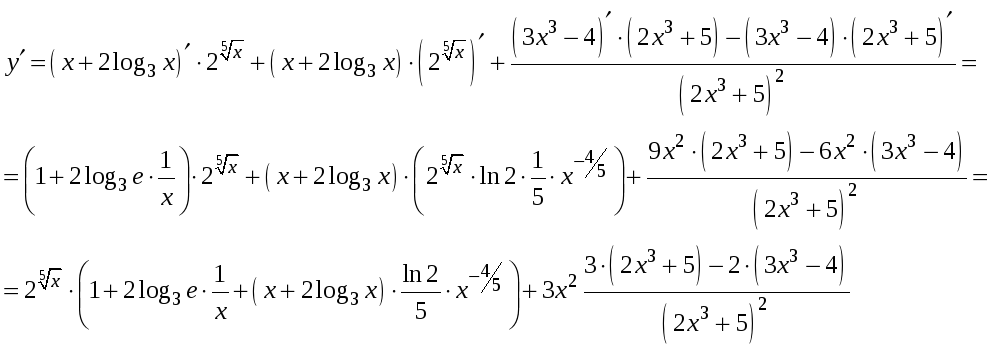
-
Точка А движется по оси абсцисс, и её координаты изменяются по формулам
![]() - время. Точка В движется по оси ординат,
её координаты изменяются по формулам
- время. Точка В движется по оси ординат,
её координаты изменяются по формулам
![]() Найти момент времени, при котором площадь
треугольника ОАВ (где О – начало
координат) минимальна.
Найти момент времени, при котором площадь
треугольника ОАВ (где О – начало
координат) минимальна.
Решение
Площадь прямоугольного треугольника
(а угол, образованный осями декартовых
координат – прямой) определяется как
половина произведения сторон –
![]()
Исследуем функцию площади на экстремум, найдём производную:
![]()
Найдём вторую производную:
![]()
Приравнивая производную нулю, находим экстремум:
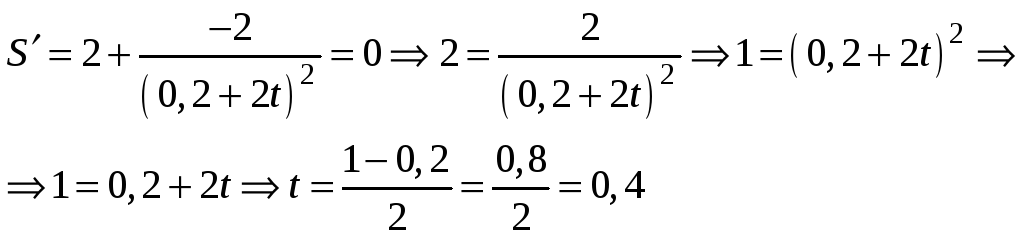
Отсюда, минимальная площадь, так как функция при t=0,4 имеет минимум (вторая производная положительна):
![]() кв.
ед.
кв.
ед.
-
Составить уравнения касательных к графику функции
 ,
перпендикулярных прямой
,
перпендикулярных прямой
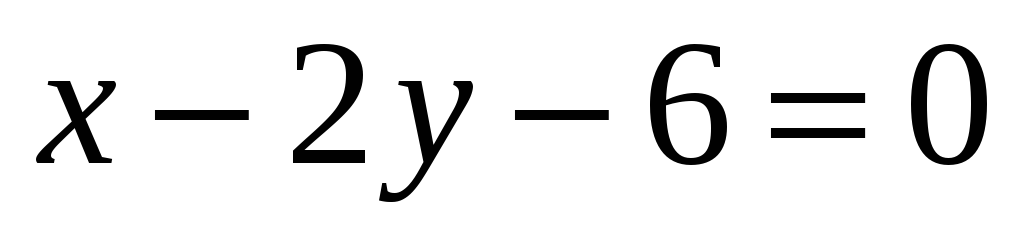 .
Сделать чертёж.
.
Сделать чертёж.
Решение
Касательными к графику функции являются
прямые с угловым коэффициентом k
равным значению производной в точке
касания. Производной функции является
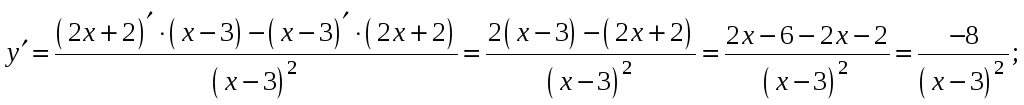
Перпендикулярность прямых (касательной
и любой другой прямой) означает равенство
единице произведения их угловых
коэффициентов:
![]() :
:
![]()
![]()
Таким образом,
![]()
Откуда
![]()
Уравнениями касательных являются уравнения прямых с заданными угловыми коэффициентами и проходящие через заданные точки:
![]()
Чертёж:
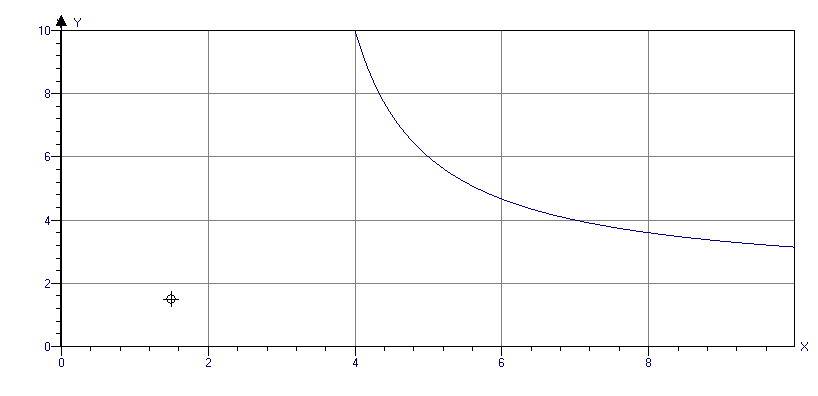
-
Исследовать функцию
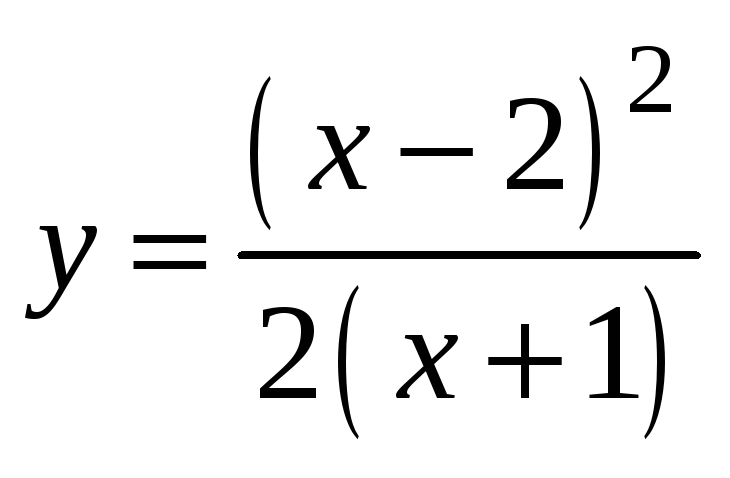 и построить схематично её график.
и построить схематично её график.
Решение
-
Областью определения данной функции является всё множество действительных чисел, за исключением точки х=-1 (выколотая точка).
-
Множеством значений данной функции является всё множество действительных чисел.
-
Точками пересечения с осями координат являются точка (0; 2) – с осью ОУ и точка (2; 0) – с осью ОХ.
-
Интервалы знакопостоянства: функция больше нуля при аргументе х большем минус единицы и меньше нуля при аргументе х меньше минус единицы:

-
Исследуем интервалы возрастания и убывания функции с помощью производной:
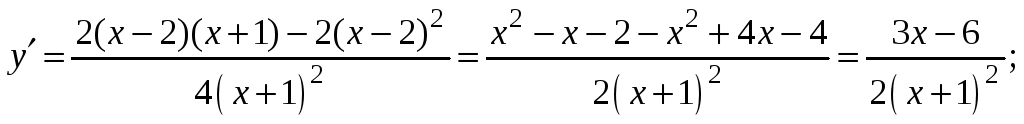
Производная равна нулю в единственной точке (2; 0). До этой точки производная отрицательна (функция убывает), после – положительна (функция возрастает).
-
Исследуем интервалы выпуклости и вогнутости функции с помощью второй производной:
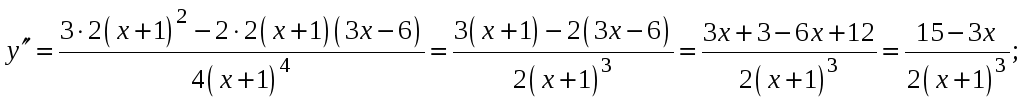
Вторая производная равна нулю в единственной точке (5;0,75). До этой точки вторая производная положительна (функция вогнута), после – отрицательна (функция выпукла). В точке х=2, вторая производная положительна, следовательно в этой точке функция имеет минимум.
-
Функция терпит разрыв в точке х=1, следовательно, функция имеет вертикальную асимптоту х=1. Горизонтальных и наклонных асимптот функция не имеет, так как
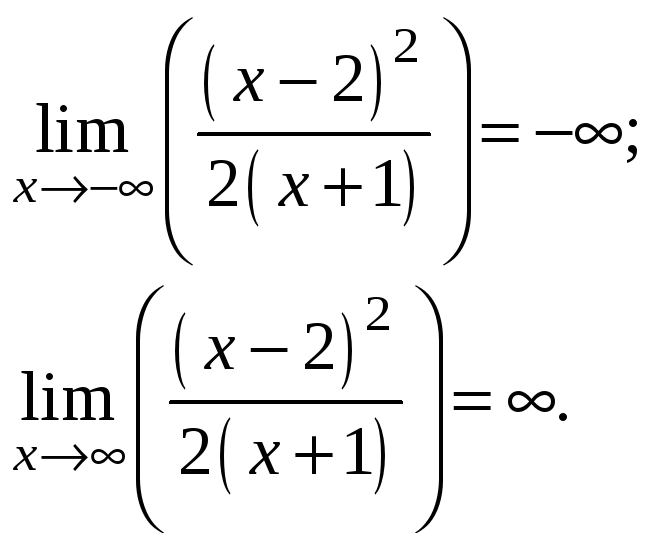
График функции: