Bilety / 15

Формула Тейлора

Определение

Пусть функция  бесконечно дифференцируема в некоторой окрестности точки . Формальный ряд

называется рядом Тейлора функции  в точке .

 

f(x) = Pn(x)

 

Если функция f(x) не является многочленом , то при всех n имеем f(x) ≠ Pn(x) и тогда

 

f(x) = Pn(x) + Rn + 1(x).

(1)

 

Это равенство называется формулой Тейлора.  В ней Rn + 1(x) — некоторая функция, называемая остаточным членом формулы Тейлора

Если x0 = 0, то формулу Тейлора называют иногда формулой Маклорена.

Полезную информацию об остаточном члене формулы Тейлора Rn + 1(x) дают следующие две теоремы. Они уточняют уточняют формулу (1).

Формула Тейлора для некоторых элементарных функций

Рассмотрим несколько важнейших элементарных функций и найдём для них многочлены Тейлора при .

1. Рассмотрим функцию . Все её производные совпадают с ней: , так что коэффициенты Тейлора в точке равны

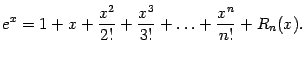
Поэтому формула Тейлора для экспоненты такова:

2. Рассмотрим функцию . Её производные чередуются в таком порядке:

а затем цикл повторяется. Поэтому при подстановке также возникает повторение:

и т. д. Все производные с чётными номерами оказываются равными 0; производные с нечётными номерами равны 1 при , то есть при , и при , то есть при . Таким образом, при всех и коэффициенты Тейлора равны

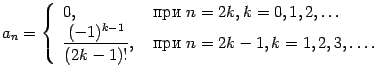
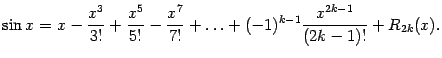
Получаем формулу Тейлора для синуса:

Заметим, что мы можем записать остаточный член вместо (как можно было бы подумать), поскольку можно считать, что слагаемое порядка , с коэффициентом, равным 0, тоже включено в многочлен Тейлора.

3. Для функции производные также чередуются с циклом длины 4, как и для синуса. Значения в точке имеют то же чередование:

Нетрудно видеть, что при , и при , . Поэтому разложение косинуса по формуле Тейлора имеет вид

Здесь мы также считаем, что последним в многочлене Тейлора выписано слагаемое, содержащее с нулевым коэффициентом.

4. Функция f(x) = (1 + x)^a.

(a - действительное число)

…………………………………………………..

Тогда:

Если в полученной формуле принять a = n, где n- натуральное число и f⁽ⁿ⁺¹⁾(x)=0, то R_n+1 = 0, тогда

Получилась формула, известная как бином Ньютона.

Пример: Применить полученную формулу для нахождения синуса любого угла с любой степенью точности.

На приведенных ниже графиках представлено сравнение точного значения функции и значения разложения в ряд Тейлора при различном количестве членов разложения.

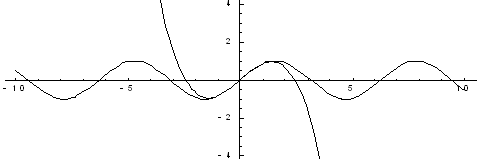
5. Функция f(x) = ln(1 + x).

 

  Получаем: f(x) = ln(1 + x); f(0) = 0;

f¢(x) = ; 

 

 

………………………………………

 

 

Итого: 

 

  Полученная формула позволяет находить значения любых логарифмов (не только натуральных) с любой степенью точности. Ниже представлен пример вычисления натурального логарифма ln1,5. Сначала получено точное значение, затем – расчет по полученной выше формуле, ограничившись пятью членами разложения. Точность достигает 0,0003.

ln1,5 = 0,405465108108164381

 

ТЕЙЛОРА МНОГОЧЛЕН

степени п для функции f. праз дифференцируемой при х=х₀ - многочлен вида

Значения Т. м. и его производных до порядка n включительно в точке х=х₀ совпадают со значениями функции и ее соответствующих производных в той же точке:

Т. м. является многочленом наилучшего приближения функции f при  в том смысле, что

и если к.-л. многочлен Q_n,(x) степени, не превышающей п, обладает тем свойством, что

где  то он совпадает с Т. м. Р _п (х). Иначе говоря, многочлен, обладающий свойством (*), единствен.  Если хотя бы одна из производных f^(k) (х), k=0, 1, . . ., п, не равна нулю в точке х ₀. то Т. м. является главной частью Тейлора формулы.