Bilety / 11

Теорема 17.1 (Теорема Ферма)

Если функция имеет производную и в точке имеет экстремум, то значение производной в этой точке равно 0.

Доказательство

Пусть - точка минимума. Тогда при . Значение выражения . Значит, . Рассмотрим теперь , при этом также , и выражение . Значит, правая производная . По теореме 14.5 . Из ранее доказанного следует: . Теорема доказана.

Геометрический смысл теоремы Ферма Существует такая точка , в которой касательная параллельна оси Ox. Замечания В точке экстремума может не быть производной. Пример: , - точка минимума, но .

2. Равность нулю производной - необходимое условие существования экстремума, но не достаточное. То есть производная может быть равной 0 и вне точки экстремума. Пример: , но точка 0 - не экстремум.

Теорема 17.2 (Теорема Ролля)

Пусть:

1. Функция 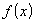непрерывна на отрезке : ;

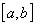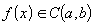2. Для любого x из интервала 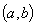существует производная: ;

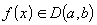3. Значения функции на концах отрезка равны: .

Тогда существует такое , что производная .

Доказательство

1. Функция непрерывна существуют .

2. Если 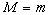, то функция 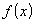является константой, и ее производная в любой точке равна 0, т.е. теорема доказана.

3. Если же , то оба значения не могут достигаться в концевых точках, т.к. 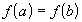и . Тогда хотя бы одно из них достигается во внутренней точке c, и, по теореме Ферма 17.1  

Замечания:

1. Существует хотя бы одна точка, в которой касательная к графику функции параллельна оси Ox (см. рисунок к теореме Ферма).

2. Все условия теоремы Ролля существенны, т.е. нельзя отбростиь хотя бы одно из них.

Примеры:

1. Отбросим условие непрерывности. Рассмотрим функцию на отрезке 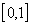. На интервале производная всюду равна 1.

2. Отбросим условие дифференцируемости. Рассмотрим функцию 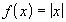. В точке , но 0 - точка минимума.

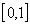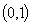3. Отбросим условие равности функции на концах отрезка. Рассмотрим функцию на отрезке . При этом производная всюду на интервале равна 1 .