1)Предел последовательности. БМП и их свойства. Элементарные способы вычисления пределов. Примеры.

Предел последовательности. Основные определения и примеры.

Определение 22 (определение последовательности). Функция f:N® X, областью определения которой является множество натуральных чисел, называется последовательностью.

Если f:N->R, то последовательность называется числовой. Иначе, числовая последовательность – это функция натурального аргумента: x_n = f(n). Обозначают числовую последовательность {x_n}. Примеры числовых последовательностей:

Пример 16. 

1) 1,2,..., n,...; 

2) 1,-1,1,-1,...,(-1)ⁿ,...;

3) 1,1/2,1/3,...,1/n,....

Определение 23.

Последовательность называется ограниченной сверху (снизу), если  M (m), такое, что для любого n N x_n M (x_nm).

Последовательность называется ограниченной, если она ограничена и сверху и снизу, то есть  c > 0 такое,

что |x_n|  c для любого n N. Заметим, что в данном определении c=max{|m|,|M|}.

Пример 17.

1,2,...,n,... — ограничена снизу, но неограничена сверху;

{1/n} – ограничена, так как 0< x_n1 ;

{(-1)ⁿ} – ограничена

Определение 24. Последовательность x_n называется неограниченной, если

 c > 0  N: |X_N| > c

Неограниченная последовательность может быть односторонне ограниченной, то есть ограниченной или сверху, или снизу. Пример неограниченной сверху последовательности: x_n = n.

Понятие предела числовой последовательности хорошо иллюстрируется на следующем примере. Пусть задана последовательность x_n = 1/n. Изобразим ее члены точками на числовой оси (рис. 12).

Можно заметить, что члены последовательности с ростом номера n как угодно близко приближаются к 0. При этом величина x_n становится все меньше и меньше. Очевидно, что пределом данной последовательности будет 0.

Дадим строгое определение предела числовой последовательности.

Определение 25 (определение предела последовательности). Число A называется пределом последовательности x_n, если

U(A)  N:  n > N x_n  U(A).

Приведем другое определение предела, которое является эквивалентным первому.

Определение 26 (определение предела последовательности). Число A называется пределом x_n, если

  > 0  N:  n > N |x_n-A |< 

Заметим, что здесь использованы логические символы: квантор всеобщности  (вместо слова "для любого") и квантор существования  (вместо слова "найдется").

Предел числовой последовательности обозначается lim_n x_n = A или x_nA при n. Последовательность, имеющая предел, называется сходящейся, в противном случае расходящейся.

Пример 18. Пусть x_n = 1/n, покажем, что

lim_n 1/n = 0.

Для этого запишем определение:

 >0  N: n>N |x_n|<.

То есть 1/n< при n>N=[1/].

Пример 19.

x_n = .

Доказать, что

lim_n  = 1

  >0  N:  n > N |-1| < .

1/n <   n > 1/N = [1/]

Если  = 1/10 , то N=10 и при n > 10 следует выполнение нужного неравенства.

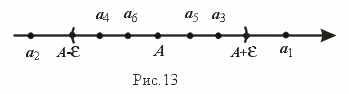
Выясним геометрический смысл понятия предела последовательности. Расположим члены последовательности x₁,x₂,..., x_n,... на числовой прямой. Неравенство |x_n-A|< равносильно следующему A-  < x_n < A + , которое говорит о том, что члены последовательности x_n попадают в  - окрестность точки A (рис.13). Вне этой  -окрестности может быть лишь конечное число членов данной последовательности.

Определение 27 (бесконечно малая последовательность).

Бесконечно малая последовательность — последовательность, предел которой равен 0. То есть

lim_n  x_n = 0 или более подробно с учетом определения предела  >0  N:  n>N |x_n| <   x_n.

Пример 20. Последовательность x_n = 1/n является бесконечно малой последовательностью.

Определение 28 (бесконечно большая последовательность). x_n – бесконечно большая последовательность, если 

 c>0  N:  n>N |x_n|>c.

Пример 21. Последовательности n, 2ⁿ являются бесконечно большими.

Следует различать неограниченную и бесконечно большую последовательности. Всякая бесконечно большая последовательность является неограниченной, однако неограниченная не обязательно является бесконечно большой. Рассмотрим следующий пример.

Пример 22. Пусть x_n = 1,1/2,3,1/3,5,1/4,..., нетрудно заметить, что данная последовательность состоит из двух составляющих, а именно Х_2k-1 = 2k-1, Х_2k = 1/(k+1). Данная последовательность неограниченная, так как содержит неограниченную составляющую Х_2k-1 = 2k-1, но не является бесконечно большой, так как содержит вторую часть Х_2k = 1/(k+1).

Очевидно следующее утверждение.

Лемма 1. Если _n — бесконечно малая последовательность, то 1/ _n —бесконечно большая последовательность.

Пример 23. Пусть _n = 1/n, которая является бесконечно малой, тогда последовательность  _n = 1/ _n = n будет бесконечно большой.

Теорема 5. Для того чтобы последовательность {x_n} имела предел, равный A необходимо и достаточно, чтобы ее члены имели вид

x_n = A+ _n,

где

lim _n   _n = 0.

Справедливы следующие свойства бесконечно малых последовательностей, которые легко получить из определения бесконечно малой последовательности.

Теорема 6. (свойства бесконечно малых последовательностей)

1. Сумма и разность двух бесконечно малых последовательностей является бесконечно малой последовательностью.

2. Произведение ограниченной последовательности на бесконечно малую последовательность является бесконечно малой последовательностью.

Следствие 1. Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью. Алгебраическая сумма конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Часть I. Основные способы вычисления пределов, содержащих неопределенности типа .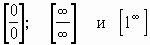

Алгоритм решения.

1. Подставить в выражение предельное значение аргумента.

2. Определить есть или нет неопределенность. Если нет, дать ответ.

3. Если неопределенность есть, то по ее виду выбрать одно из правил устранения этой неопределенности.

4. Преобразовать выражение согласно выбранному правилу, и к новой форме предела применить данный алгоритм, начиная с п.1.

Правило 1.

 В числителе и знаменателе вынести x в максимальной степени, если это возможно. Заметим, что , а  , где c - любое число.

Правило 2.

 Числитель и знаменатель разделить одновременно на , если это возможно. Необходимо иметь в виду, что , а  , где c - число, отличное от нуля.

Правило 3.

При вычислении пределов от иррациональных выражений, не попадающих в предыдущие правила, следует избавиться от корней, входящих в неопределенность. Возможны следующие способы:

3.1. замена переменной  , позволяющая извлечь корни, входящие в неопределенность;

3.2. дополнение до формулы, позволяющей возвести корень в соответствующую ему степень; здесь используются формулы:  ; .

Например,  , т.е. умножили и разделили на сопряженное выражение.

Правило 4.

При наличии неопределенности в пределе от выражения, содержащего тригонометрические функции, следует выделить в этом выражении первый замечательный предел:

 .    (1)

Можно использовать следствия этого предела:

 ;     (2)  ;     (3)  ;     (4)  .     (5)

Правило 5.

Вычисление предела сложнопоказательной функции. .

Если рассматриваемый предел содержит неопределенность  , то он сводится ко второму замечательному пределу:

     (1) или   .     (2)

Правило 6.

Предел сложной функции:.

В частности, , если.

Необходимо помнить свойства логарифмов : , , , . Есть пределы, которыми можно пользоваться как "табличными":

,     (1) ,     (2) ,     (3) .     (4)

Часть II. Вычисление пределов функций с помощью правила Лопиталя-Бернулли.

Правило 7.

Правило Лопиталя-Бернулли: 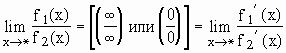  , т.е. предел отношения функций, стремящихся одновременно к бесконечности или к нулю (являющихся одновременно бесконечно большими или бесконечно малыми), равен пределу отношения их производных.

Правило 8.

Если при вычислении  получается неопределенность типа  , то можно использовать правило Лопиталя, преобразовав предварительно выражение следующим образом:  или .

Правило 9.

Если при вычислении  получается неопределенность одного из следующих типов , ,  , то можно использовать правило Лопиталя, преобразовав предварительно выражение следующим образом: 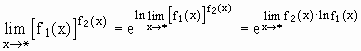 , где  вычисляется по Правилам 7, 8 . В некоторых случаях полезно комбинировать правило Лопиталя-Бернулли с элементарными тождественными преобразованиями, рассмотренными в части I.