
Ситуационные задачи
1.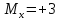 .;
2.
.;
2.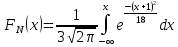 ; 3.
; 3.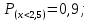 4.
4.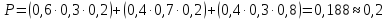 ;
5.
;
5. ;
6.
;
6.
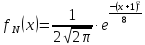 ;
7.
;
7.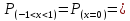 0,1;
8.
0,1;
8.
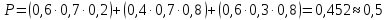 ; 9.C
= 8; 10.Указание:
при построении графиков необходимо
учесть общий характер функции
распределения вероятностей и тот факт,
что стандартное отклонение определяет
тангенс угла наклона графика функции
распределения вероятностей в точке
соответствующей математическому
ожиданию.;
; 9.C
= 8; 10.Указание:
при построении графиков необходимо
учесть общий характер функции
распределения вероятностей и тот факт,
что стандартное отклонение определяет
тангенс угла наклона графика функции
распределения вероятностей в точке
соответствующей математическому
ожиданию.;
11.
|
F(x) |
0,00 |
при x ≤ -2 |
|
|
0,05 |
при -2 < x ≤ -1 | ||
|
0, 20 |
при -1 < x ≤ 0 | ||
|
0,30 |
при -0 < x ≤ +1 | ||
|
0,80 |
при +1 < x ≤ +2 | ||
|
1,00 |
при x > +2 |
12.
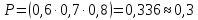 ;13.
;13.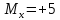 ;
14.
;
14.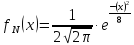 ;
15.
;
15.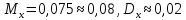 ;
16.
;
16.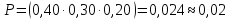 ;
;
17.
Математическое
ожидание М(х) случайной величины Х
(отклонение диаметра шарика от проектного
размера) М(х) = 0. Стандартное отклонение
σ = 0,4 задано по условию задачи. Тогда: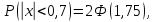 где
где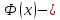 функция
Лапласа. По таблице (см. Справочные
материалы №4) находим:
функция
Лапласа. По таблице (см. Справочные
материалы №4) находим:
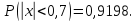 Следуя
классическому определению вероятности:
Следуя
классическому определению вероятности: ,
,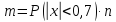 .
Дляn
= 100 и
.
Дляn
= 100 и
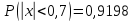 получаемm=91,98
≈ 92.
получаемm=91,98
≈ 92.
18.
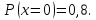 19.
19.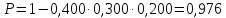 .
20.
.
20.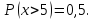
21. 1). Событие А - сигнальная лампочка прибора с перегорает при включении в сеть. 2). Найдём вероятность события противоположного событию А. Р(«не А») = 1 – Р(А) = 1 – 0,1 = 0,9. 3). Событие «лампочка не перегорает при первом включении» и событие «лампочка перегорает при втором включении» являются независимыми. Можно применить формулу умножения вероятностей для независимых событий. 4). Р(АВ) =Р(А) Р(В) . 5). Искомая вероятность Р = 0,9 0,1 = 0, 09
22.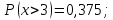 23.
М(х)
= 0,1; 24.
23.
М(х)
= 0,1; 24.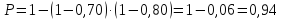 ;
25.М(х)
= 0;
;
25.М(х)
= 0;
26.
1).
Пусть случайным событием А является
рождение мальчика. 2). Согласно
статистическому определению вероятности:
Р(А) =
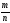 ,
гдеm
- число рождений мальчиков, n
- суммарное число рождений мальчиков
и девочек. 3). Событие – «рождение
девочки» является противоположным
событию А.
,
гдеm
- число рождений мальчиков, n
- суммарное число рождений мальчиков
и девочек. 3). Событие – «рождение
девочки» является противоположным
событию А.
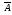 - случайное событие - рождение девочки.
4). Вспомнив аксиому сложения вероятностей:
- случайное событие - рождение девочки.
4). Вспомнив аксиому сложения вероятностей: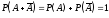 5).Найдём
вероятность рождения девочки
5).Найдём
вероятность рождения девочки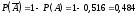
27.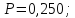 28.
28.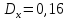 ;
29.
;
29.
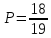 ;
30.
;
30.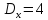 ;
;
31. 1). В данном случае надежность системы представляет событие – «хотя бы один блок работает». 2). Событие противоположное событию – «хотя бы один блок работает» Это - «Ни один из блоков не работает». 3). События образуют полную группу попарно несовместных событий.
4).
Применяя формулу сложения вероятностей
для случая полной группы попарно
несовместных событий:
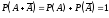 .
5). Надёжность системы:
.
5). Надёжность системы: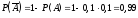
32.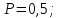 33.
33.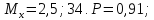 35.
35.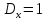 ;
;
36. 1). Событие А - событие, состоящее в том, что после 3 игр в коробке не останется не игранных мячей. 2). А = А1 × А2 × А3, где А1 – событие, состоящее в то, что для первой игры взяты три не игранных мяча. А2 - событие, состоящее в то, что для второй игры взяты три не игранных мяча. А3 - событие, состоящее в то, что для третьей игры взяты три не игранных мяча. 3). А1 - событие, равное произведению трёх событий В1 , В2 и В3. В1 - событие «первый мяч для первой игры оказался не игранным», В2 - событие «второй мяч для первой игры оказался не игранным» и В3 - событие «третий мяч для первой игры оказался не игранным».4). Р(А1) = (9/9) ×(8/8)×(7/7); Р(А2) = (6/9) ×(5/8)×(4/7) ; Р(А3) = (3/9) ×(2/8)×(1/7). 5). По формуле умножения вероятностей для зависимых событий Р(А) = Р(А1) × Р(А2) × Р(А3) = (9/9) × (8/8) ×(7/7) × (6/9) ×(5/8) × (4/7) × (3/9) ×(2/8)×(1/7) » 0,003

