6.2. Сокращённая днф. Метод Квайна.

Определение 1. Элементарным произведением называется конъюнкт, в который любая переменная входит не более одного раза. Формула (х₁, х₂, … х_п) называется импликантой формулы (х₁, х₂, … х_п), если   элементарное произведение и для соответствующих формулам  и  функций f_ и f_ справедливо неравенство f_f_. Формула (х₁, х₂, … х_п) называется импликантой функции f, если   импликанта совершенной ДНФ, представляющей функцию f. Импликанта (х₁, х₂, … х_п)=формулы называется простой, если после отбрасывания любой литеры из  не получается формула, являющаяся импликантой формулы . Дизъюнкция всех простых импликант данной формулы (функции) называется сокращённой ДНФ.

Пример 6.1. Найдем все импликанты, простые импликанты и сокращённую ДНФ функции ху. Всевозможные элементарные произведения от переменных х и у  это в точности следующие: х, у, ,,ху, у, х,. Построим для самой функции и для этих элементарных произведений таблицу истинности:

х	у	ху	х	у			ху	у	х
0	0	0	0	0	1	1	0	0	0	1
0	1	1	0	1	1	0	0	1	0	0
1	0	1	1	0	0	1	0	0	1	1
1	1	1	1	1	0	0	1	0	0	0

Сравнивая значения элементарных произведений со значениями функции ху, заключаем, что импликантами этой функции являются в точности х, у, ху, у, х, так как для всех них выполнено условиехуf_, где f_  одна из х, у, ху, у, х(например,хух). Из этих импликант простыми являются толькох и у. Действительно, удаление одной из литеры в импликантах ху, у, хведёт к получению других, а именно х или у. Таким образом, сокращённой ДНФ функции является ху (что, впрочем, следует из определения самой функции).

В качестве другого примера отметим, что всевозможными импликантами функции ху являются у, х, из которых все являются простыми, и, следовательно, сокращённой ДНФ являетсяух.

Ясно, что с помощью таблицы истинности при большом числе переменных построение сокращённой ДНФ становится проблематичной. Существуют специальные методы, позволяющие избегать работы с таблицами истинности. Они основаны на следующих операциях замены подформул, формул, выражающих функции, им эквивалентными подформулами:

АхАА  операция полного склеивания;

АхАААхА операция неполного склеивания;

Ах^АА  операция элементарного поглощения (0, 1)

Упражнение 6.1.Найти сокращённые ДНФ функций из упражнения 5.1.

Решение. а) Применим к СДНФ функции сначала операцию неполного склеивания, а затемэлементарного поглощения:

zyxzzzyxzzy.

В результате получили сокращённую ДНФ функции.

(1) К паре конъюнктов zиxz(точнее, к их дизъюнкции) применили операцию неполного склеивания:zxzz. Больше пар, к которым можно применить эту операцию, нет.

(2) К парам (z,z) и (z,xz) применили операцию элементарного поглощения: zzzи zxzz..

Ответ: zy.

6.3. Минимальная ДНФ. Таблица Квайна. Рассмотрим ещё

Пример 6.2. Пусть функция f(x, y, z) задана совершенной ДНФ f(x, y, z)=zxxy. Производя над ней операции склеивания и элементарного поглощения, получаем её сокращённую ДНФf(x, y, z)=x. Построив её таблицу истинности, можно убедиться, что импликантуможно удалить, то естьf(x, y, z)=x, и сокращённую ДНФ функции можно упрощать дальше, удаляя лишние импликанты.

Определение 2. Тупиковой ДНФ называется ДНФ, которая получается из сокращённой ДНФ удалением всех лишних импликант, не меняя таблицу истинности. Минимальной ДНФ функции называется её тупиковая ДНФ с наименьшим числом вхождений переменных.

Одним из способов получения минимальной ДНФ из сокращённой ДНФ является использование так называемой таблицы Квайна (ТК). Заголовками столбцов ТК являются конституенты единицы СДНФ, а заголовками строк  простые импликанты из сокращённой ДНФ. Таблица заполняется знаками «+» на пересечениях тех строк и столбцов, для которых конъюнкт, стоящий в заголовке строки, входит в конституенту единицы, являющейся заголовком столбца. В тупиковую ДНФ выбирается минимальное число тех простых импликант, знаки «+» при которых охватывают все столбцы ТК.

ТК для функции примера 6.2 имеет вид

		z	x	xy
	+	+
	+		+
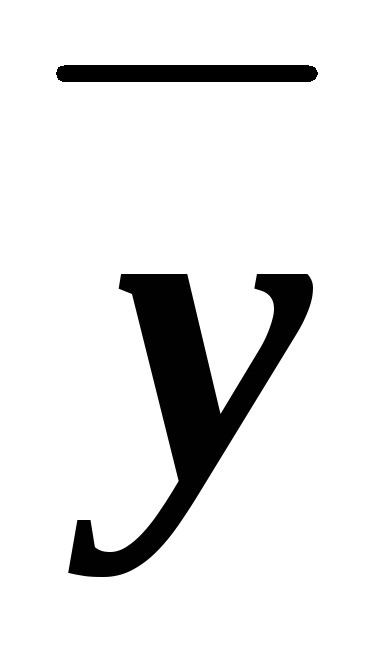
x			+	+

Минимальное число простых импликант, знаки «+» при которых охватывают все столбцы, образуют импликанты первой и третьей строки, то есть иx. Поэтомуxявляется МДНФ функции.

Упражнение 6.2.Найти все тупиковые и минимальные ДНФ функций упражнения 5.1.

6.4. Метод Квайна-Мак-Класки. При больших п (порядка 4) метод Квайна становится громоздким. Существует ряд модификаций метода, позволяющих технически упростить данный метод. Опишем один из методов, называемых методом Квайна-Мак-Класки.

Сначала заметим, что при операции склеивания склеиваются элементарные произведения, отличающиеся только одной литерой. Это и положено в основу модификации. Алгоритм метода  следующий:

1. Представим каждую конституенту булевой функции в виде двоичного набора длины п.

2. Сгруппируем наборы так, чтобы в каждую группу попали те и только те наборы, которые имеют одинаковое число единиц, располагая их в порядке возрастания числа единиц.

3. Сравнивая наборы из соседних групп, выделяем пары, отличающиеся только в одной позиции (тем самым выделяем конституенты, отличающиеся только одной литерой).

4. В обоих выделенных наборах пар заменяем отличающиеся символы (0 и 1) на «-» (тем самым из двух различных наборов получаем один и тот же набор из 0, 1 и «-», что соответствует тому, что два одинаковых элементарных произведения склеили по отличающейся литере, при этом знак «-» соответствует тому, что соответствующая литера в полученном элементарном произведении будет отсутствовать).

Если в результате склеивания получается уже имеющийся набор, то результат склеивания (то есть полученный набор) опускается (это соответствует тому, что согласно закона идемпотентности одинаковые элементарные произведения сливаются в одну). Если в результате склеивания получаются наборы, отличающиеся только в одной позиции, причём в соответствующей позиции одного стоит знак «-» (у других  0 или 1), то остальные опускаются (что соответствует элементарному поглощению)

5. После всевозможных склеиваний на очередном этапе, переходим к пункту 2.

Процесс продолжается до тех пор, пока склеивать будет нечего. Простыми импликантами являются те элементарные произведения, которые не участвовали в процессе склейки на очередном шаге.

Пример 6.3. Проиллюстируем метод на примере функции, имеющей систему равенств f(0, 1, 0)=f(0, 1, 1)=f(1, 0, 1)=f(1, 1, 0)=f(1, 1, 1)=1 примера 6.2. Располагать группы и результаты всех шагов удобно в таблице. Кроме того, наборы, участвующие при склейке на очередном шаге, будем как-то помечать, например, знаком «*». Тогда после конечного шага все наборы, не участвовавшие при склейке на очередном шаге, останутся непомеченными.

В

	I шаг	II шаг
010*	01-* -10*	-1-
011* 101* 110*	-11* 1-1 11-*
111*

результате первого шага мы склеили: 1) наборы 010 и 011, получили 01-; 2) наборы 010 и 110, получили -10; 3) наборы 011 и 111, получили -11; 4) 101 и 111, получили 1-1; 5) наборы 110 и 111, получили 11-. Во втором шаге склеиваются: 1) наборы 01- и 11-, получается -1-; 2) наборы -10 и -11, получается -1- (который уже есть). После второго шага склеивать нечего. В итоге непомеченными оказываются -1- и 1-1. Это означает, что соответствующие им элементарные произведенияу и хz являются простыми импликантами функции. Таким образом, сокращённой ДНФ данной функции является ухz.

Заметим, что для удобства в таблице Квайна при обозначении элементарных произведений также удобно использование наборов из 0 и 1. Так, таблица Квайна для нашего примера выглядит следующим образом:

	010	011	101	110	111
-1-	+	+		+	+
1-1			+		+

Из таблицы видим, что полученная сокращённая ДНФ является минимальной, и даже тупиковой.

Упражнение 6.3.Найти все тупиковые и минимальные ДНФ функций упражнения 5.2.

Решение. б) Применяя модификацию метода Квайна, находим сокращённую ДНФ.

	Iшаг	IIшаг
0000*	-000 000-
0001* 1000*	10-0* 1-00*	1--0
0110* 1010* 1100*	011-* -110* 1-10* 11-0*	-11-
0111* 1110*	-111* 111-*
1111*

Она же оказыется тупиковой и минимальной, в чем легко убедиться, построив таблицу Квайна:

	0000	0001	0110	0111	1000	1010	1100	1110	1111
1--0					+	+	+	+
-11-			+	+				+	+
-000	+				+
0001		+