Лабораторная работа №1 свободные колебания в контуре

ЦЕЛЬ РАБОТЫ – Изучение процесса свободных колебаний в последовательном колебательном контуре цепи, содержащей индуктивность, емкость и активное сопротивление.

ОСНОВНЫЕ ПОЛОЖЕНИЯ

Свободными колебаниями называют процессы в линейных электрических цепях, не содержащих внешних источников, но которые в начальный момент времени имеют некоторый начальный запас энергии.

Последовательный колебательный контур представляет собой цепь, содержащую, последовательно соединенные емкость C, индуктивность L и резистивность R. Наличие в контуре реактивных элементов C и L, придает ему возможность запасать одновременно энергию электрического и магнитного полей. При определенных условиях в контуре возможно возникновение колебаний за счет обмена энергией между емкостью и индуктивностью.

Простейший способ возбуждения свободных колебаний состоит в зарядке конденсатора от стороннего источника напряжения и разрядке конденсатора на LCR-цепь (рис. 1.1).

Рис. 1.1. Схема зарядки и разрядки конденсатора

Пусть при конденсатор заряжается от источника напряженияE. В момент времени конденсатор, предварительно заряженный до напряжения, переключателемSA подключается к цепи, состоящей из L и R. Электрическое состояние цепи в каждый момент времени , на основании второго закона Кирхгофа, описывается уравнением. Используя связь между напряжением и током на элементах цепиL, R, C получим интегро-дифференциальное уравнение:

. (1.1)

Выполнив дифференцирование по времени и освободившись от коэффициента при второй производной, имеем:

. (1.2)

Введя обозначения ,, уравнение (1.2) удобно представить в виде

. (1.3)

Для анализа свободных колебаний в контуре необходимо решить уравнение (1.3), которое является линейным дифференциальным уравнением второго порядка. Уравнение (1.3) удовлетворяется решением вида в предположении, чтоp является одним из корней характеристического уравнения

. (1.4)

Уравнение (1.4) имеет два корня

. (1.5)

В силу линейности уравнения (1.3), его общее решение представляет собой сумму двух слагаемых:

. (1.6)

Произвольные постоянные А₁ и А₂ определяются из начальных условий. В начальный момент времени имеем:,. Начальное условие для производной тока определим из уравнения Кирхгофа, справедливого и для момента времени:, откуда. Подставив начальные условия для тока и его производной в (1.6) получим систему двух алгебраических уравнений:

(1.7)

Ее решением является

. (1.8)

Подставив формулы (1.8) в (1.6) получаем временную зависимость тока, которая описывает свободный процесс изменения тока в контуре

. (1.9)

Проанализируем полученный результат. Исследуя корни характеристического уравнения (1.4) можно видеть, что корни (1.5) могут быть:

1. при простыми действительными:

2. , ,

где , причем;

2) при кратными действительными();

3) при комплексно-сопряженными,, где.

Эти три условия, с учетом связи ,с величинамиL, R, C и воспользовавшись такими основными характеристиками колебательного контура как характеристическое сопротивление и добротность , могут быть записаны следующим образом:

1) или, или;

2) или, или;

3) или, или.

В первом случае, когда , ток в контуре описывается выражением

. (1.10)

Из графика этой зависимости (рис. 1.2) видно, что при больших потерях , в контуре нет колебательного процесса, а наблюдается так называемый апериодический режим собственных колебаний. Это означает, что в этом режиме не происходит колебательного обмена энергией между конденсатором и индуктивностью.

Рис.1.2. Апериодический режим собственных колебаний ()

Во втором случае, когда , зависимость изменения тока от времени можно определить как предел выражения (1.10) при :

. (1.11)

Как и в первом случае, здесь сохраняется апериодический характер изменения тока. Второй режим является граничным между апериодическим и колебательным режимами, и поэтому его называют критическим.

В третьем случае, когда , активное сопротивление контура меньше удвоенного волнового и добротность, вконтуре наблюдается колебательный режим. Для подтверждения этого подставим комплексно-сопряженные корни в общее решение (1.9) и получим

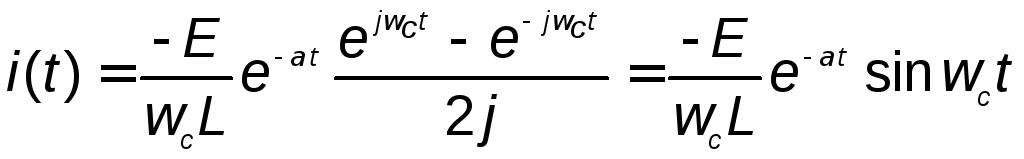. (1.12)

Рассчитанная по формуле (1.12) зависимость тока от времени (рис. 1.3) показывает, что разрядка конденсатора в контуре с представляет собой затухающий колебательный процесс. Колебание описывается зависимостью, где–частота собственных колебаний в контуре с потерями.

Сомножитель указывает на то, что амплитуда колебаний уменьшается по экспоненциальному закону. Уменьшение амплитуды колебаний характеризует коэффициент затухания.

Рис. 1.3. Затухающий колебательный процесс ()

При экспериментальном исследовании свободных колебаний в контуре обычно наблюдают напряжение. Приведем напряжение на индуктивности для колебательного режима

, (1.13)

где .

В радиоэлектронике часто применяют колебательные контуры с малыми потерями, в которых сопротивление потерь значительно меньше характеристического сопротивления. При достаточно высокой добротностичастота собственных колебаний в контуре с малыми потеряминезначительно отличается от частоты собственных колебаний в идеальном контуре без потерь

, (1.14)

поэтому при колебательном разряде частоту собственных колебаний в контуре можно определить по приближенной формуле:

и 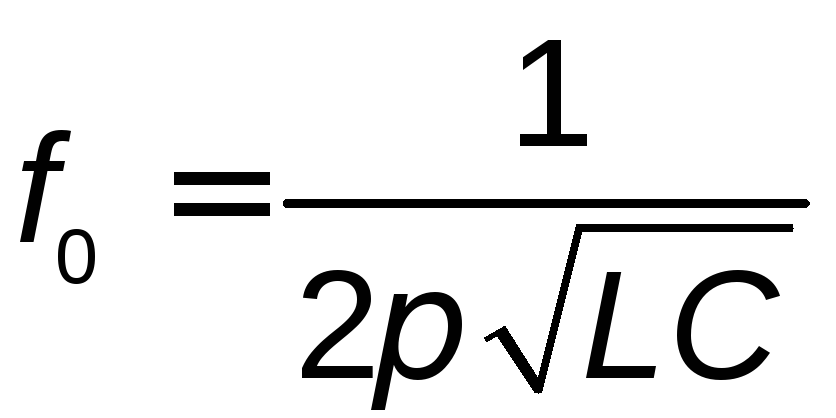. (1.15)

Для характеристики уменьшения амплитуды колебаний во времени вводят коэффициент , который называетсядекрементом затухания. Декремент затухания удобно находить как отношение двух амплитуд напряжения, взятых на интервале времени, равному одному периоду колебания (рис. 1.4)

. (1.16)

На практике удобнее логарифмический декремент затухания:

. (1.17)

Величина логарифмического декремента затухания связана с параметрами колебательного контура

. (1.18)

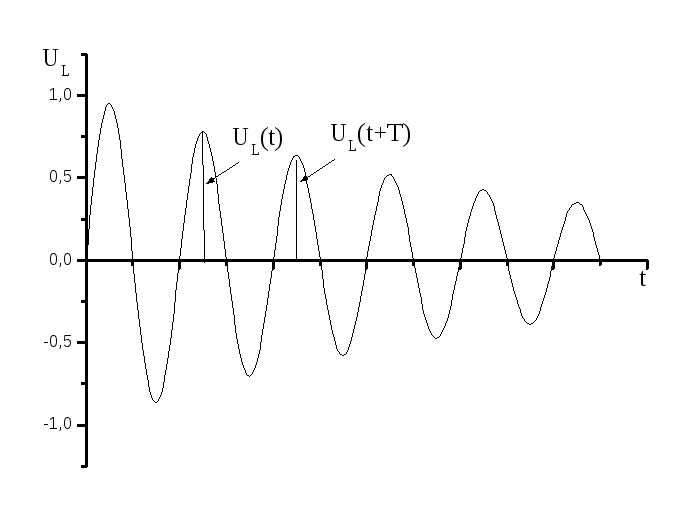
Рис. 1.4. Определение декремента затухання по осциллограмме напряжения

Логарифмический декремент затухания колебательного контура с малыми потерями может быть найден как относительное убывание амплитуды колебаний:

(1.19)

Величина, в раз меньшая логарифмического декремента, называется затуханием:

. (1.20)

Затухание есть величина обратная добротности, и поэтому по измеренным значениям затухания можно определить добротность колебательного контура:

. (1.21)

ПОДГОТОВКА К РАБОТЕ

1. Изучить теоретический материал по теме лабораторной работы.

2. Самостоятельно выполнить вывод формул, описывающих различные режимы свободных колебаний в контуре с потерями.

3. Вычислить частоты свободных колебаний для контуров с заданными =13 мГн и=0,5; 1,0; 1,5; 2,0; 4,0 мкФ.

4. Для заданных =13 мГн и=0,5; 1,0; 1,5; 2,0; 4,0 мкФ вычислить значения характеристического сопротивления.

5. По найденным значениям характеристического сопротивления для R=0,5; 10; 15; 20; 30; 50; 80; 100; 150 Ом рассчитать добротности. Определить значения добротности, при которых возможен колебательный режим, а при которых – апериодический режим.

6. Подготовить ответы на контрольные вопросы.

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Лабораторная установка питается от сети напряжением 220 В. Она состоит из стабилизированного источника питания, релаксационного генератора, тороидальной катушки индуктивности, набора емкостей и резисторов с возможностью переключения, которые смонтированы на общем шасси.

Принципиальная схема лабораторной установки приведена на рис. 1.5. Стабилизированный источник питания содержит однополупериодный выпрямитель, выполненный на диоде VD типа Д7Ж, сглаживающий фильтр на С₁ и стабилизатор напряжения, выполненный на стабилитроне VL₁ типа СГ-4С. Релаксационный генератор на управляемой лампе тлеющего разряда VL₂ типа МТХ-90 необходим для многократного повторения процесса, что дает возможность наблюдать свободные колебания с помощью электронного осциллографа.

Рис. 1.5. Принципиальная схема установки

ЛАБОРАТОРНОЕ ЗАДАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

1. Включая поочередно емкости для нескольких значений сопротивления магазина, получить колебательный разряд в контуре. Измерить величину соседних амплитуд затухающих колебаний и зарисовать осциллограммы.

2. Подбирая сопротивление магазина, получить граничный режим работы контура (апериодический процесс при наименьшем контура) для всех значений емкости контура.

3. Определить с помощью осциллографа частоты свободных колебаний при всех значениях емкости контура и сравнить с расчетными.

4. Вычислить логарифмические декременты затухания, добротности, пользуясь полученными результатами измерений.

5. Определить собственное (без магазина) активное сопротивление контура (для разных значений емкости ).

СОДЕРЖАНИЕ ОТЧЕТА

1. Результаты подготовки к работе.

2. Результаты исследований, полученные при выполнении работы (расчетные данные, графики).

3. Выводы, поясняющие полученные результаты.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие процессы в линейных электрических цепях называют свободными колебаниями?

2. Дайте определение и укажите физический смысл таких параметров контура как декремент затухания, логарифмический декремент затухания, затухание, добротность, характеристическое сопротивление.

3. От чего зависит частота свободных колебаний в контуре с потерями?

4. Поясните физику процессов в контуре при апериодическом режиме.

5. Изложите физику процессов в контуре при колебательном режиме.

6. Укажите назначение элементов схемы лабораторного макета (Рис.5) и поясните принцип получения свободных колебаний.

ЛИТЕРАТУРА: [3], [8], [11].