2. Связанные контуры

В целях частотной селекции широко используются также системы связанных контуров, обладающие лучшими характеристиками по сравнению с одиночными контурами.

Два контура называют связанными, если изменение электрического состояния одного контура вызывает соответствующее изменение состояния другого контура. На рис. 2.6 приведены схемы двухконтурных колебательных систем с индуктивной и емкостной связью. Степень связи контуров определяется коэффициентом связи . Для двух индуктивно связанных контуров коэффициент связи равен.

В общем случае, используя понятие комплексного сопротивления, систему двух связанных контуров можно представить эквивалентной схемой рис. 2.7.

а) б)

Рис.2.6. Связанные колебательные контуры:

а) индуктивная связь,

б) емкостная Т-образная связь

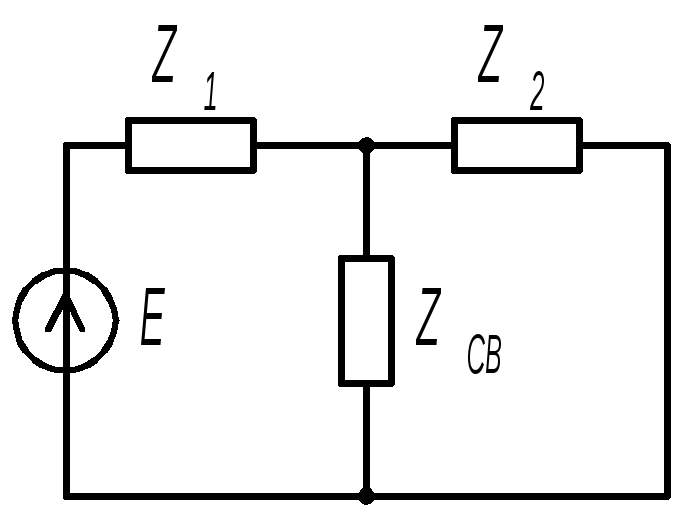
Рис. 2.7. Эквивалентная схема системы связанных контуров

Система контурных уравнений для этой цепи в комплексной форме имеет вид:

(2.17)

Здесь ,– собственные сопротивления первого и второго контуров;=– взаимное сопротивление контуров – сопротивление связи, которое обычно является реактивным:

. (2.18)

При условии (2.18) коэффициент связи определяется отношением

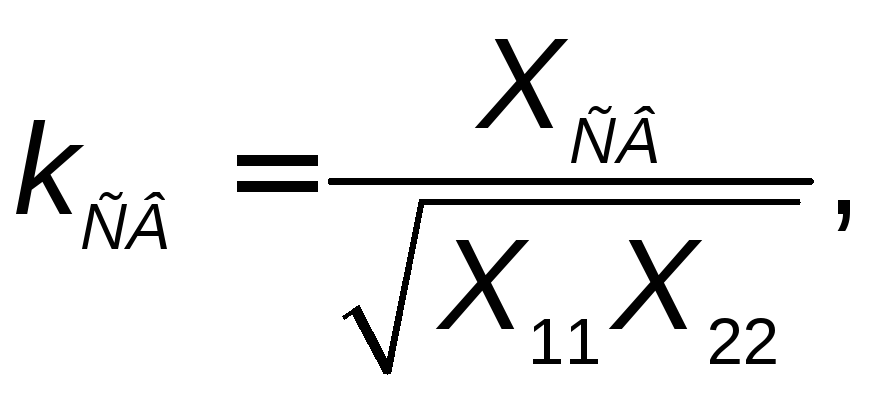(2.19)

где и– реактивные сопротивления контуров, одноименные с элементом связи.

Если в качестве реакции рассматривается колебание тока в первом контуре , то цепь характеризуется комплексной входной проводимостью, которая определяется выражением

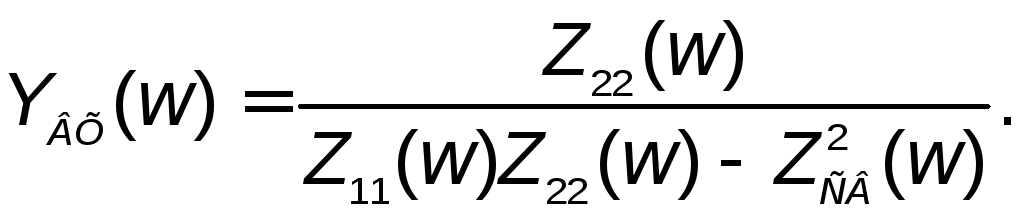(2.20)

Если в качестве реакции рассматривается колебание тока во втором контуре , то характеристикой цепи является комплексная передаточная функция

(2.21)

Часто в качестве входной функции системы связанных контуров рассматривают входное сопротивление

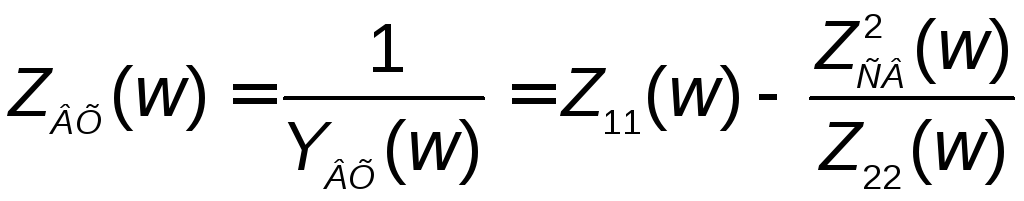. (2.22)

В этом выражении первое слагаемое – собственное сопротивление первого контура, а второе слагаемое – сопротивление, называемое "вносимым". При условии (2.18)

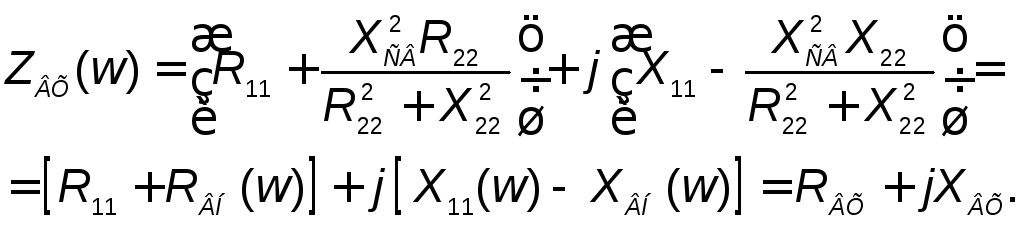(2.23)

Активная часть вносимого сопротивления , учитывающая потери энергии во втором контуре, увеличивает активную составляющую входного сопротивления. Реактивная часть вносимого сопротивления, определяющая запасаемую во втором контуре энергию, изменяет реактивную составляющую входного сопротивления и описывает изменение резонансных свойств первого контура под влиянием второго.

Резонансные частоты двухполюсной цепи определяются уравнениями (2.4). В рассматриваемом случае имеем:

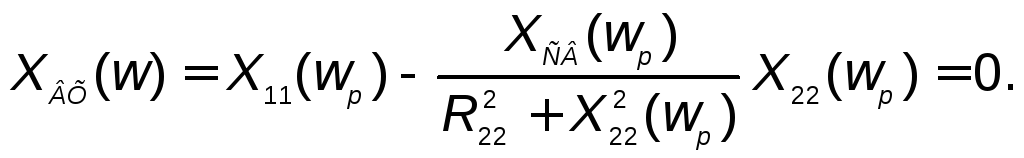(2.24)

Уравнение (2.24), достигающее пятой степени, может иметь до трех вещественных корней в зависимости от соотношений коэффициента связи и других параметров контуров. При фиксированном коэффициенте связинастройка системы двух связанных контуров в резонанс на заданную частоту может быть достигнута несколькими способами. Во-первых, этого можно достичь настройкой каждого контураотдельно в резонанс ,(полный резонанс). Во-вторых, при расстроенных контурахиизменением величиныили, т.е. регулировкой реактивных элементов первого или второго контура, добиваются.

Обычно настройка системы связанных контуров на колебание заданной частоты имеет своей целью получение максимальной амплитуды тока во втором контуре, т.е. обеспечение максимального значения передаточной функции в (2.21). Для получения наибольшего из всех возможных максимумов необходимо не только настроить систему двух связанных контуров в резонанс, но и подобрать оптимальную связь между ними.

Полным резонансом называют способ настройки, при котором сначала порознь настраиваются в резонанс и первый, и второй контуры, а затем подбирается оптимальная связь ().

Сложным резонансом называется такой способ настройки, при котором в системе из двух расстроенных контуров добиваются максимальной амплитуды тока во втором контуре путем настройки системы в резонанс регулировкой реактивных элементов одного из контуров и подбором оптимальной связи.

Из анализа передаточной функции (2.21) можно показать, что оптимальная настройка системы контуров способом сложного резонанса достигается при более сильной связи между контурами, чем при настройке способом полного резонанса ().

Для системы из двух одинаковых контуров при полном и сложном резонансе максимальные амплитуды тока имеют одинаковые значения

, т.е. .

Проанализируем частотные характеристики связанных контуров. Для системы двух индуктивно связанных контуров (рис. 2.8) входное сопротивление связи в общем случае равно .

Рис. 2.8. Система двух индуктивно связанных контуров

Рассмотрим случай, когда коэффициент взаимной индукции положительный, а контуры одинаковые. Если в качестве реакции рассматривается напряжение на емкости второго контура, то передаточная функция на основании (2.21) определяется выражением, которое можно представить произведением функций вида (2.2), соответствующих одиночным контурам, настроенным на различные частоты:

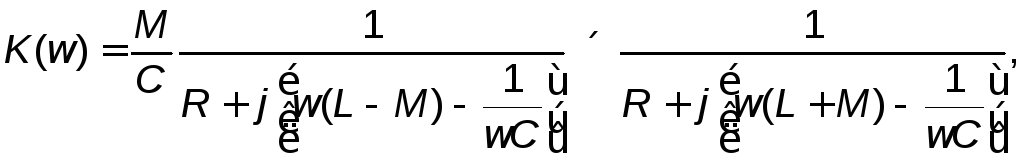(2.25)

а с учетом того, что и,

(2.26)

Из анализа выражения (2.26) следует, что в зависимости от величины коэффициента связи графики АЧХ (рис. 2.9) могут иметь вид одногорбой кривой при малых значенияхи двугорбой кривой при достаточно больших значениях. Причем превращение одногорбой кривой АЧХ для передаточной функции (2.26) в двугорбую происходит, когда.

Как было показано выше на примере одиночного колебательного контура (п.1), значения резонансных частот не всегда совпадают с частотами, соответствующими максимумам передаточных функций. Это явление имеет место и по отношению к входной проводимости системы контуров. Действительно, уравнение, определяющее резонансные частоты (2.24), при имеет один вещественный корень, а при– три вещественных корня:

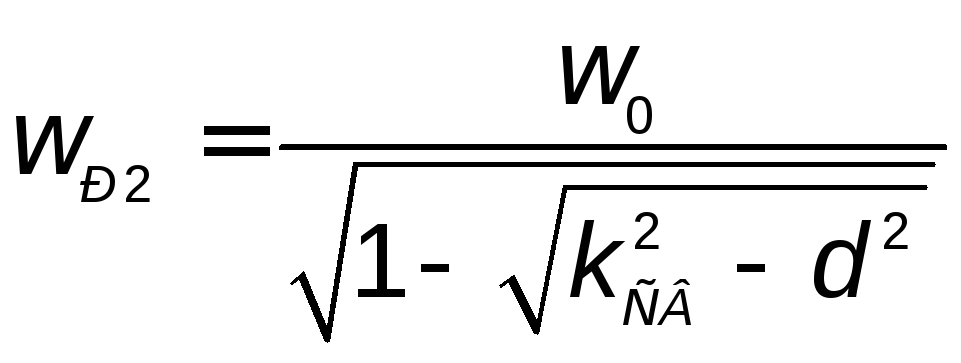, , . (2.27)

Рис. 2.9. Вид АЧХ двух связанных колебательных контуров

при разных коэффициентах связи

Полоса пропускания АЧХ существенно зависит от степени связи контуров. При слабой связи, когда , полоса пропусканияприблизительно равна полосе пропускания одиночного контура, т.е.При критической связи, , а график АЧХ имеет вид одногорбой кривой с плоской вершиной. Предельным значением коэффициента связи, при котором провал между горбами графика АЧХ опускается до 0,707, является величина, при такой связи . На рис. 2.9 приведены графики АЧХ для различных значенийи для сравнения приведен график АЧХ одиночного контура (пунктирная линия).

Значительная полоса пропускания, дополнительная возможность регулирования ее ширины и более крутые скаты частотной характеристики являются основными преимуществами связанных контуров по сравнению с одиночными контурами при осуществлении частотной селекции сигналов.

ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ

Лабораторная установка представляет собой панель с расположенными на ней переменными конденсаторами и катушками индуктивности, расстояние между которыми можно изменять. Схема соединения деталей изображена на поверхности панели. Кроме макета в состав лабораторной установки входят также измерительный генератор и лампово-полупроводниковый вольтметр.

ПОДГОТОВКА К РАБОТЕ

1. Изучить теоретический материал по теме лабораторной работы.

2. Для одиночного последовательного и параллельного колебательного контура определить комплексные входные сопротивления и построить их АЧХ.

3. Нарисовать в рабочей тетради схемы систем из двух колебательных контуров с различными видами связи.

4. Для системы двух индуктивно связанных контуров определить входное сопротивление и на его основе показать способы настройки системы в резонанс.

5. Подготовить ответы на контрольные вопросы.

ЛАБОРАТОРНОЕ ЗАДАНИЕ И МЕТОДИЧЕСКИЕ УКАЗАНИЯ

1. Исследование одиночного колебательного контура

С помощью клеммы разомкнуть цепь второго колебательного контура и развести катушки индуктивности на максимальное расстояние.

1.1 Для одиночного колебательного контура экспериментально снять амплитудно-частотную характеристику для значения емкости , указанногое преподавателем.

1.2 Построить графики снятой зависимости и определить величины полосы пропускания и значения добротности. Экспериментальное значение добротности сравнить с расчетным по заданным ,,.

2. Исследование связанных колебательных контуров

2.1 Для указанного на макете значения частоты генератора при фиксированной связи между контурами снять экспериментальные настроечные кривые и. Построить графики снятых зависимостей и объяснить полученные результаты.

2.2 Осуществить настройку связанных контуров методом сложного резонанса на значение частоты колебаний, указанное преподавателем. В процессе настройки снять экспериментальную зависимость , где– расстояние между катушками индуктивности. Определить, соответствующее максимальному значению измеряемого напряжения.

2.3 Для того же значения частоты колебаний осуществить настройку связанных контуров методом полного резонанса. В процессе настройки снять экспериментальную зависимость . Определить оптимальное значение. Сопоставить и объяснить результаты, полученные в 2.2 и 2.3.

2.4 Для системы связанных контуров, настраиваемой методом полного резонанса, снять экспериментальные амплитудно-частотные характеристики для случаев ,,. Построить графики снятых зависимостей и объяснить полученные результаты.

СОДЕРЖАНИЕ ОТЧЕТА

1. Результаты подготовки к работе.

2. Результаты исследований, полученные при выполнении работы (расчетные данные, графики).

3. Выводы, поясняющие полученные результаты.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Какие виды резонансов наблюдаются в последовательном и параллельном колебательных контурах? Какую частоту принято считать резонансной?

2. Дайте определение полосы пропускания контура. Как полоса пропускания связана с его добротностью? Физический смысл добротности.

3. Какие виды связи применяются между колебательными контурами? Дайте определение коэффициента связи.

4. Поясните экспериментальные настроечные кривые.

5. Сопоставьте и объясните результаты, полученные при настройке контуров методами полного и сложного резонансов.

6. Объясните резонансные явления в индуктивно связанных контурах.

ЛИТЕРАТУРА: [2] – [5], [8].