Почленное интегрирование степенного ряда

Теорема. Пусть степенной ряд

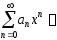
имеет интервал сходимости 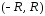, и функция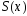— его сумма. Если отрезоксодержится в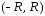, точисловой ряд , составленный из интегралов отдельных слагаемых, сходится, и его сумма равна 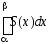,то есть

.

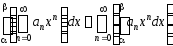10. Степенные ряды в окрестности произвольной точки.

рассмотрим степенной ряд

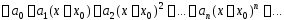. (1)

Введем новую переменную . Тогда ряд (1) примет вид:

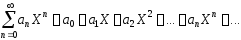(2)

• ряд в окрестности точки . Пусть— его интервал сходимости. Тогда ряд (2) абсолютно сходится при

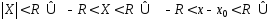
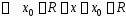
и расходится при 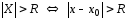. Поэтому интервал сходимости степенного ряда (1) в окрестности произвольной точки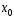получается из интервала сходимости степенного ряда (2) с теми же коэффициентами, но в окрестности нулевой точки, смещением середины интервала сходимости в точку. Радиус сходимости по-прежнему может быть найден по формуле

Ряд Тейлора функции

Определение.Пусть функция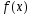является бесконечно дифференцируемой в окрестности точки.Рядом Тейлораэтой функции называется степенной ряд по степеням, коэффициентами которого являются коэффициенты Тейлора:

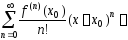
. (1)

Достаточное условие разложимости функции в ряд Тейлора

Теорема. Пусть в окрестност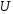и точки производные всех порядков функции ограничены одним и тем же числом: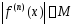при всех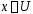и при любом. Тогда функция разлагается вв ряд Тейлора(то есть ее ряд Тейлора

сходится при всех 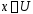, и его сумма равна).

11.Разложение элементарных функций в ряд Маклорена

1. Рассмотрим показательную функцию . При всехимеем: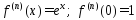. Ряд Маклорена имеет вид:

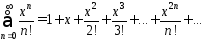
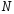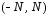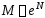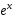Для каждого натурального при всех. По достаточному условию разложимости, выполненному для интервалаи для, функцияразлагается в ряд Маклорена в интервале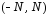, а значит, и на.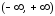

Показательная функция раскладывается на в степенной ряд вида:

.

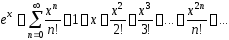12. Рассмотрим функцию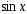. Последовательно дифференцируя, получаем:

…

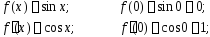
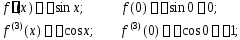
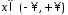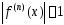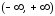и т.д. Через каждые четыре дифференцирования производные повторяются. Производные всех порядков при всех ограничены:. Поэтомуфункция раскладывается нав степенной ряд; разложение содержит только нечетные степени и имеет вид:

.

3. Рассмотрим функцию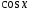. Последовательно дифференцируя, получаем:

…

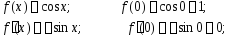
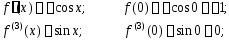
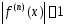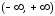и т.д. Через каждые четыре дифференцирования производные повторяются. Производные всех порядков при всех ограничены:. Поэтомуфункция раскладывается нав степенной ряд; разложение содержит только четные степени и имеет вид:

.

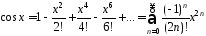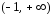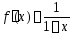13. Рассмотрим функциюс областью определения. Ее производная. Функция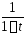является при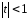суммой бесконечно убывающей геометрической прогрессий с начальным членом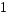и знаменателем:

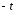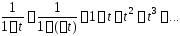
Проинтегрируем это равенство почленно по направленному отрезку , где: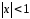

.

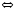
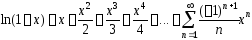Разложение справедливо при 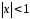. Можно показать, что оно сохраняется и при.

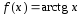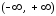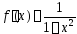14. Рассмотрим функциюс областью допустимых значений. Ее производная. Функция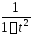является при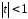суммой бесконечно убывающей геометрической прогрессий с начальным членоми знаменателем:

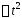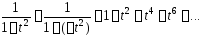
Проинтегрируем это равенство почленно по направленному отрезку , где:

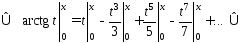
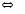
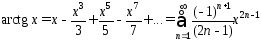. (37)

При 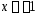в правой части равенства (37) имеем знакочередующийся ряд, который сходится по признаку Лейбница. Можно показать, что в этих точках сохраняется равенство (37). Приполучаем:

.