39

1.Сходимость числового ряда

Определение. Числовым рядом называется выражение

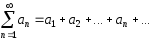(1)

Определение. 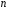–й частичной суммой ряда (1) называется сумма 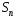первых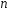членов ряда:

.

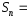
Так,

;

;

…

;

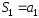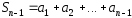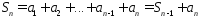. (2)

Определение. Если существует конечный предел последовательности частичных сумм:

,

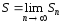то говорят, что ряд (1) сходится, а число 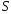— его сумма. Если предел бесконечен или не существует, то говорят, что ряд расходится.

Необходимый признак сходимости ряда

Теорема. Если числовой ряд 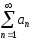сходится, то предел его общего члена равен нулю:.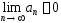

Доказательство. Пусть ряд 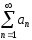сходится, и его сумма равна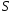: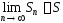. Тогда из равенства (2) следует:

.

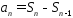Отсюда по свойствам предела:

. ■

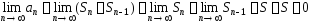2. Ряд, образованный геометрической прогрессией

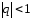Ряд, образованный геометрической прогрессией со знаменателем , сходится, если, и расходится, если.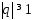

3. Арифметические свойства сходящихся рядов

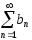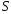Теорема. Пусть ряды исходятся, и их суммы равны, соответственно,и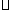. Тогда рядыи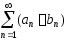, полученные почленным сложением и вычитанием исходных рядов, также сходятся, и их суммы равны, соответственно,и.

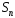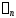Доказательство. Пусть и— частичные суммы исходных рядов. Тогда числаи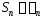являются частичными суммами рядов, полученных почленным сложением и вычитанием. По свойствам предела:

. ■

Теорема. Пусть ряд сходится, и его сумма равна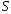. Тогда ряд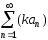, полученный почленным умножением исходного ряда на постоянное число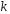, также сходится, и его сумма равна.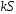

Доказательство. Пусть 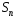— частичная сумма исходного ряда. Тогда частичная сумма нового ряда:

.

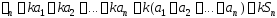Поэтому

. ■

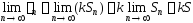Итак, сходящиеся ряды можно почленно складывать, вычитать и умножать на постоянное число.

4. Признаки сравнения положительных рядов

Будем рассматривать ряды с положительными членами

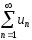(8)

и

, (9)

Теорема (признак сравнения по неравенству). Пусть при всех 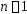выполняется неравенство: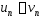. Тогда:

1) если ряд (9) с бóльшими членами сходится, то ряд (8) с меньшими членами также сходится;

2) если ряд (8) с меньшими членами расходится, то ряд (9) с бóльшими членами также расходится.

Теорема (предельный признак сравнения). Пусть существует конечный предел

,

и ряд (9) сходится. Тогда ряд (8) также сходится.

Радикальный признак сходимости Коши

Теорема. Пусть для ряда 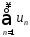с положительными членами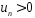, существует предел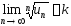. Тогда при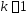ряд сходится, а приряд расходится.

Интегральный признак сходимости Коши

Теорема. Пусть для ряда с положительными членами 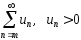, существует функция, удовлетворяющая трем условиям:

1) при некотором натуральном 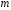функция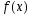непрерывна на;

2) 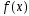монотонно убывает на;

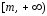3) члены ряда являются значениями этой функции при це-

лых значениях аргумента: .

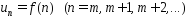Тогда ряд сходится или расходится одновременно с несобственным интегралом .

5. Знакочередующиеся ряды

Определение. Пусть задана последовательность 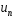, в которой все члены положительны. Ряды

(1)

и

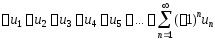(2)

называются знакочередующимися

Теорема  (признак  Лейбница). Пусть члены знакочереду- ющегося ряда (1) удовлетворяют двум условиям:

1. модули членов ряда монотонно убывают:

;

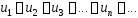2) .

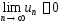Тогда ряд (1) сходится, и его сумма 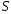удовлетворяет неравенству(для ряда (2), соответственно, ).
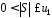