
- •Киевская государственная академия водного транспорта
- •Введение
- •Глава 1. Ориентирование наблюдателя на земной поверхности
- •1.1. Фигура и размеры Земли
- •Дополнительные данные к эллипсоиду Красовского
- •1.2. Основные точки, линии и плоскости на поверхности Земли
- •1.3. Географические координаты. Разности широт и долгот
- •1.3.1. Географические координаты
- •1.3.2. Разности широт и долгот
- •1.3.3. Задачи на расчет значений () а. Расчет значений разности широт () и разности долгот ()
- •Б. Расчет значений широты () и долгот () пункта прихода
- •1.4. Радиусы кривизны земного эллипсоида
- •Глава 2. Определение направлений в море
- •2.1. Основные линии и плоскости наблюдателя
- •2.2. Системы счета направлений
- •2.2.1. Круговая система счета
- •2.2.2. Полукруговая система счета
- •2.2.3. Четвертная система счета
- •2.2.4. Румбовая система счета (рис. 2.6)
- •2.2.5. Задачи на перевод направлений в круговую систему счета
- •2.3. Истинные направления и их соотношения
- •2.3.1. Истинный курс, истинный пеленг, курсовой угол
- •2.3.2. Задачи на расчет значений ик, ип, ку
- •2.4.2. Дальность видимости ориентиров в море
- •2.4.3. Дальность видимости огня ориентира, показанная на карте (рис. 2.16)
- •2.4.4. Задачи на расчет дальностей видимости а) Видимого горизонта (De) и ориентира (dп)
- •Б) Открытие огня маяка
1.3.3. Задачи на расчет значений () а. Расчет значений разности широт () и разности долгот ()
|
№ задачи |
1 |
2 |
3 |
4 | |
|
Дано |
|
60˚15,2′ N |
41˚02,4′ N |
13˚01,9′ N |
38˚49,3′ S |
|
|
2˚40,4′ W |
17˚21,3′ E |
93˚54,3′ E |
72˚19,6′ E | |
|
|
19˚15,2′ N |
8˚58,6′ N |
24˚36,2′ S |
41˚24,7′ N | |
|
|
10˚14,6′ E |
52˚38,7′ W |
114˚08,5′ W |
89˚05,4′ W | |
|
Ответ |
|
41˚00,0′ к S |
32˚03,8′ к S |
37˚38,1′ к S |
80˚14,0′ кN |
|
|
12˚55,0′ к E |
70˚00,0′ к W |
151˚57,2′ к E |
161˚25,0′ к W | |
|
№ задачи |
5 |
6 |
7 |
8 | |
|
Дано |
|
13˚58,6′ N |
15˚21,3′ S |
26˚27,6′ N |
76˚40,5′ S |
|
|
120˚25,5′ E |
60˚21,5′ E |
99˚13,7′ E |
59˚00,5′ W | |
|
|
36˚01,4′ S |
55˚48,7′ N |
19˚48,5′ N |
81˚21,3′ N | |
|
|
131˚40,5′ W |
122˚03,0′ E |
91˚56,3′ W |
18˚25,4′W | |
|
Ответ |
|
50˚00,0′ к S |
71˚10,0′ к N |
6˚39,1′ к S |
158˚01,8′ кN |
|
|
107˚54,0′ кE |
61˚41,5′ кE |
168˚50,0′ кE |
40˚35,1′ кE | |
Б. Расчет значений широты () и долгот () пункта прихода
|
№ задачи |
1 |
2 |
3 |
4 | |
|
Дано |
|
21˚18,3′ N |
19˚19,0′ S |
57˚14,3′ N |
37˚18,9′ S |
|
|
71˚21,8′ W |
37˚16,5′ W |
157˚48,5′ W |
29˚13,4′ E | |
|
|
39˚18,3′ кS |
19˚39,0′ кN |
59˚05,4′ кS |
46˚15,1′ кN | |
|
|
97˚58,2′ кW |
56˚23,5′ кE |
32˚11,5′ кW |
47˚32,8′ кW | |
|
Ответ |
|
18˚00,0′ S |
0˚20,0′ N |
1˚51,1′ S |
8˚56,2′ N |
|
|
169˚20,0′ W |
19˚07,0′ E |
170˚00,0′E |
18˚19,4′W | |
|
№ задачи |
5 |
6 |
7 |
8 | |
|
Дано |
|
56˚00,5′ S |
13˚15,1′ S |
41˚42,1′ N |
12˚00,4′ S |
|
|
158˚34,0′ E |
5˚16,9′ W |
140˚13,9′ W |
34˚16,4′ E | |
|
|
67˚21,0′ кN |
63˚25,9′ кS |
42˚14,5′ кS |
67˚15,0′ кN | |
|
|
101˚26,0′ кE |
17˚25,6′ кE |
56˚40,5′ кW |
49˚05,5′ кW | |
|
Ответ |
|
11˚20,5′ N |
76˚41,0′ S |
0˚32,4′ S |
55˚14,6′N |
|
|
100˚00,0′ W |
12˚08,7′ E |
163˚05,6′ E |
14˚49,1′ W | |
1.4. Радиусы кривизны земного эллипсоида
Плоскости секущие эллипсоид вращения по различным направлениям, образуют в пересечении с его поверхностью или окружности или эллипсы.
Основными сечениями эллипсоида являются (рис. 1.5):
сечение плоскостью, проходящей через малую ось;
сечение плоскостью, перпендикулярной малой оси;
нормальное сечение.
Сечение плоскостью, проходящей через малую ось РРэллипсоида, образует на его поверхностимеридианный эллипсилиистинный меридиан«PQPQ». Кривизна его – переменная величина (радиус кривизныМ– тоже).Радиус М уменьшается с уменьшением географической широты ()и вычисляется по формуле:
![]() (1.4)
(1.4)
где а– большая полуось;
е– эксцентриситет![]()
Приняв, что
![]() ,
то
,
то
![]() (1.5)
(1.5)
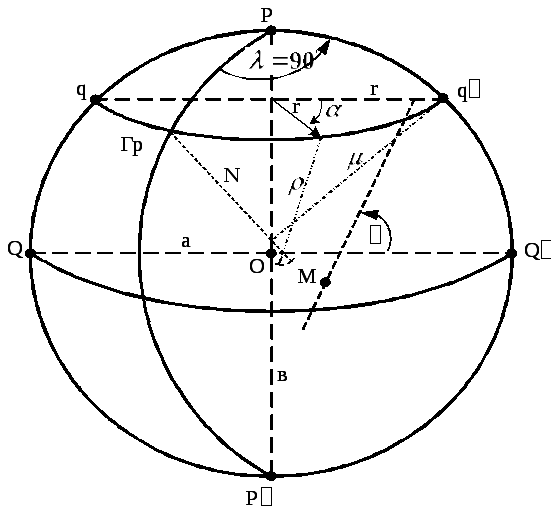
Рис.1.5. Радиусы кривизны земного эллипсоида
Экваториальный радиус кривизны меридиана при = 0: М0 = 6 335 552,6 м.
Сечение эллипсоида плоскостью перпендикулярной его малой осиРРдает на его поверхности малый кругqq–параллель. Радиус параллелиrвычисляется по формуле:
![]() или
или![]() или
или![]() . (1.6)
. (1.6)
При = 0радиус параллели равен большой полуосиаэллипсоида, и эта параллель –земной экватор.
Нормальное сечение– сечение эллипсоида плоскостью, проходящей через нормаль к его поверхности. Из бесчисленного множества возможных нормальных сечений выделяют два главных нормальных сечения –меридианноеи перпендикулярное ему – сечениепервого вертикала. Для сеченияпервого вертикаларадиус кривизны эллипсаN, вычисляется по формуле:
![]() или
или![]() (1.7)
(1.7)
на полюсе M = N, M N;
на экваторе N0 = a.
Экваториальный радиус кривизны первого вертикала при = 0:
N0 = a = 6 378 245 м.
Радиус кривизны нормального сечения,составляющего с меридианом в заданной точке уголА, вычисляется по формуле:
![]() (1.8)
(1.8)
где МиN– величины, определяемые в зависимости от широтыпо формулам (1.4) и (1.7).
Радиусом средней кривизныэллипсоида в данной точке с широтойназывают среднее геометрическое из радиусаМиN.
Радиус средней кривизны эллипсоидавычисляется по формуле:
![]() (1.9)
(1.9)
Значения М, N, R даны в картографических таблицах УГС через каждые 30 .
Произведение любого радиуса кривизны на «arс1» равно длине дуги в 1 данного сечения. Учтя приведенные выше формулы, получим выражение для определения длин дуг:
– одной минуты параллели:
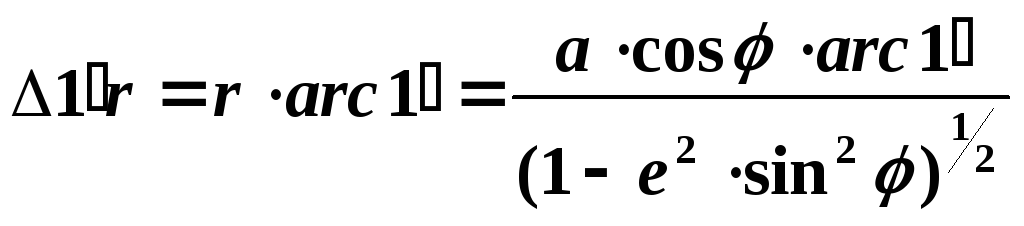 (1.10)
(1.10)
или без учета сжатия Земли (е= 0)
![]() (1.11)
(1.11)
– одной минуты первого вертикала:
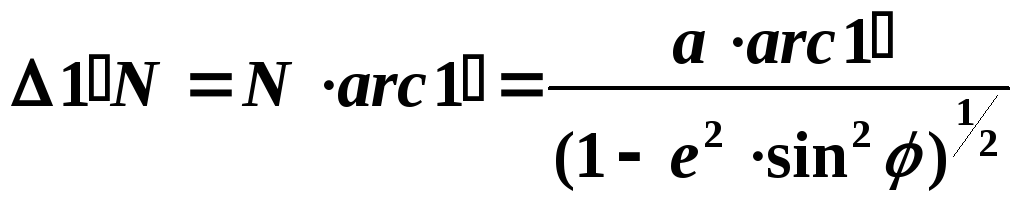 (1.12)
(1.12)
или приближенно:
![]() (1.13)
(1.13)
– одной минуты меридиана:
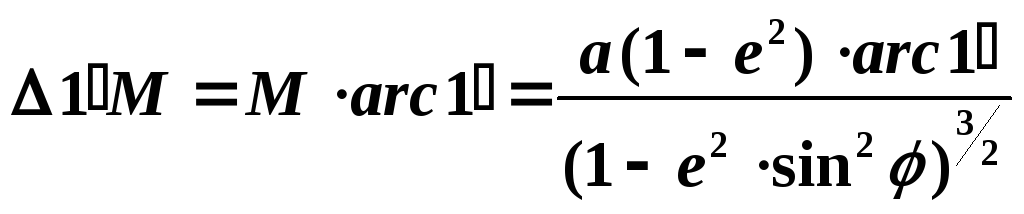 (1.14)
(1.14)
или приближенно:
![]() . (1.15)
. (1.15)
Таким образом, поверхность земного эллипсоида имеет кривизну, изменяющуюся от точки к точке по широте и от направления в данной точке.
Выводы
Для решения задач судовождения Земной шар принимается за эллипсоид вращения с элементами референц-эллипсоида Красовского.
Положение точки на земной поверхности определяется географическими координатами:
географической широтой ();
географической долготой ().
Величинами, характеризующими изменение географических координат при переходе судна от одной точки к другой, являются:
разность широт (,РШ) и
разность долгот (,РД).
Форма и размеры земного эллипсоида характеризуются радиусами кривизны его основных сечений (М, r, N, A, R).
Примечание:Самоконтроль знаний по теме проводится по тестовым заданиям к главе на базе приложения «Компьютерная система тестирования знаний «OPENTEST»».
