Lektsii_po_algebre_i_geometrii_Chast1_3

Данный курс лекций читался автором студентам факультета вычислительной техники РГРТА в 2002-2005 г.г. Автор выражает свою признательность студентам ФВТ Андриановой Евгении и Смирновой Анне за предоставленную возможность использовать в работе конспекты данных лекций, и благодарит Тиханкина Александра, Семенову Светлану, Серегину Олесю, и студентов 443 группы ФВТ, взявших на себя труд по набору текста данного материала. Также автор благодарит доцента кафедры высшей математики Тарасова Вячеслава Владимировича за предоставленную возможность использовать материал его конспекта лекций по алгебре в данной работе, и за ряд ценных замечаний и советов.

ГЛАВА 1 ВВЕДЕНИЕ В АЛГЕБРУ

§1. Элементы математической логики

Логика является наукой о законах, формах и приемах мышления. Владение приемами правильного мышления, знание логических законов, совершенно необходимы в науке. Математическая логика изучает логику, используя при этом математические методы исследования: формализацию предмета, определение основных понятий, строгое доказательство результатов. Определим некоторые основные понятия математической логики.

Под высказываниями мы будем понимать такие предложения, которым мы можем однозначно приписать логические значения: истина или ложь.

Например, фразы «где находится цирк?», «бесконечное множество точек», «исключительное явление» не являются высказываниями. Также не является высказыванием утверждение «идёт дождь», для того чтобы превратить эту фразу в высказывание необходимо, очевидно, уточнить, когда и где он идет. «Дважды два равно пяти», «если х = 2, то х2 = 4» – примеры ложного и, соответственно, истинного высказываний. Высказывания можно подразделить на простые и составные. Последние два примера являются иллюстрацией. Из простых высказываний (а также и из составных) с помощью логических операций можно составлять новые, более сложные высказывания, логические значения которых будут определяться значениями входящих в них составных частей. Например, «солдат спит, а служба идет» – составное высказывание, которое будет истинным только в случае правдивости обеих его частей.

Договоримся обозначать простые высказывания буквами: А,B,C,D.… Тогда каждое составное высказывание можно будет задать с помощью формулы, состоящей из букв, обозначающих некоторые высказывания, знаков логических операций, и скобок, определяющих порядок выполнения операций. Приведем определения основных логических операций над высказываниями.

1. Конъюнкцией высказываний A и B (варианты обозначений: A&B, A/\B – читается “A и B”) называется новое высказывание, которое истинно тогда и только тогда, когда A и B являются истинными.

2. Дизъюнкцией высказываний A и B (обозначается: A\/B – читается “A или B”) – называется новое высказывание, которое ложно тогда и только тогда, когда и A и B являются одновременно ложными.

3. Отрицанием A (варианты обозначений: Ā, ¬A – читается “не А”) называется высказывание, которое истинно тогда и только тогда, когда исходное высказывание ложно.

4. Импликацией высказываний A и B (обозначается: А → В - читается «из А следует В», “если А, то В”) называется высказывание, которое ложно тогда и только тогда, когда A истинно, а B ложно.

При этом А будем называть посылкой, а В – следствием, заключением.

5. Эквивалентностью (эквиваленцией) высказываний А и В (варианты обозначений: А~В, А↔В - читается “А эквивалентно В”, “А тогда и только тогда, когда В”) называется высказывание, которое истинно тогда и только тогда, когда А и В имеют одинаковые логические значения.

Все вышесказанное мы можем отразить в так называемой «таблице истинности».

Данные логические операции отражают наши правила логических рассуждений, умозаключений. Например, на практике мы используем правило вывода «modus pones»: (А, А→В) В, т.е. из истинности высказывания А и истинности импликации А→В следует истинность утверждения В.

Заметим, что данные операции над высказываниями могут быть точно также определены и в том случае, когда высказывания являются составными.

Договоримся в дальнейшем под формулой алгебры высказываний понимать конечную последовательность, состоящую из букв, обозначающих высказывания, знаков логических операций и скобок, определяющих порядок их выполнения. Таким образом, как каждое составное высказывание мы можем в алгебре высказываний записать в виде формулы, так и наоборот, каждая формула определяет некоторое соответствующее ей высказывание. Две формулы P и Q (и, соответственно, определенные ими высказывания) будем называть равносильными, или эквивалентными, если они принимают одинаковые значения истинности при любых одинаковых наборах значений истинности высказываний, составляющих эти формулы. Условие равносильности будем обозначать: P Q. Таким образом, например, из приведённой таблицы истинности следует, что (А→В) (Ā\/В). Очевидно, P Q тогда и только тогда, когда эквиваленция P~Q является истинной. Заметим также, что если в любой формуле мы заменим некоторое из составляющих её высказываний на равносильное, то получим формулу, равносильную исходной. Пусть P – некоторая формула. Если при любых логических значениях входящих в неё высказываний, значение P является истинным, то высказывание P называется

тождественно истинным или тавтологией.

Рассмотрим теперь предложения, которые содержат переменные, определенные на некоторых множествах значений. Если при подстановке в предложение вместо переменных конкретных их значений мы будем получать всякий раз высказывание, то такие предложения мы будем называть предикатами. Например, предложение «х>2», при х, пробегающем множество целых чисел, является предикатом. Если предложение содержит n переменных (которые могут пробегать различные множества), то говорят, что задан n - местный предикат. Например «x+y = z», где x R, y Q, z N – трехместный предикат. Если на множестве X задан предикат P(x), то выражение ( x) P(x) означает высказывание «для всех x выполняется P(x)», а выражение ( x) P(x)

– высказывание «существует x, для которого верно P(x)».

Знак – квантор всеобщности, а – квантор существования.

В множестве всех предикатов также определяются логические операции: конъюнкция,

P(x) Q(x), который обращается в ложное высказывание для тех и только тех x X, для которых P(x) и Q(x) являются ложными, т.е. значение полученного предиката при конкретном значении переменной будет вычисляться исходя из значений исходных предикатов для данного значения переменной. Также, как и для высказываний, аналогичным образом определяются и формулы логики предикатов, и понятие равносильности формул; т.е. мы должны в уже приведённом выше определении формулы заменить слово “высказывания” на слово “предикаты”, а предикаты P(x) Q(x), если для любых значений переменной полученные высказывания будут равносильными.

Приведем некоторые тавтологии алгебры высказываний.

1)(¬(¬A)) A – закон двойного отрицания.

2)(A A) A,

(A A) A – законы идемпотентности.

3)(A B) (B A),

(A B) (B A) – законы коммутативности.

4) ((A B) C) (A (B C)),

((A B) C) (A (B C)) – законы ассоциативности.

____ _ _

5)(A B) (A B),

_____ _ _

(A B) (A B) – законы обращения ( Де Моргана).

6)((A B) C) ((A C) (B C)),

((A B) C) ((A C) (B C)) – законы дистрибутивности.

7)((A B) A) A,

((A B) A) A – законы поглощения.

(( x)P(x)) (( x)P(x)) – законы обращения кванторов.

Для доказательства формул (1 – 7) достаточно составить таблицы истинности левой и правой частей и убедится в их совпадении. Также, можно доказывать равносильность, показывая, что из истинности (ложности) правой части следует и истинность (ложность) левой и наоборот. На практике применение этих законов позволяет значительно упрощать, сокращать логические формулы.

§2. Элементы теории множеств

Множество обычно определяется как произвольная совокупность объектов, называемых его элементами. Однако подобные определения чреваты неприятными последствиями типа парадокса Рассела, который мы приведем. Будем принадлежность элемента а множеству А обозначать: а A.

Пусть R - множество, элементами которого являются все множества, не являющиеся своими элементами, то есть R = {A A A}. Очевидно R не пусто, назовем его множеством Рассела. Тогда,

если R R , то R R , поскольку все составляющие R элементы удовлетворяют этому условию, следовательно, данное предположение неверно. Но, если R R , то R R , следовательно, и это предположение неверно.

Чтобы избежать этого противоречия, мы договоримся иметь дело только с теми множествами, которые сами являются элементами некоторых классов, которые и будут являться произвольными совокупностями объектов. Таким образом, определим множество как класс, который является элементом некоторого класса. Тогда парадокс Рассела превращается в утверждение, что класс Рассела R не является множеством.

Договоримся также считать, что все рассматриваемые нами множества являются подмножествами некоторого множества U , которое мы будем называть универсальным множеством. Определим теперь основные понятия теории множеств.

Будем говорить, что множество A включается в множество B , и обозначать A B , если каждый элемент множества A является элементом множества B .

Множества А и В называют равными, если они состоят из одних и тех же элементов, то есть

множество А\В состоит из всех тех элементов множества А, которые не являются элементами множества В. Разность А\А очевидно не содержит ни одного элемента, договоримся считать ее так называемым пустым множеством и обозначать . Для любого множества А, A .

Дополнением множества А будем называть множество A =U \ A , состоящее из всех тех элементов, которые не являются элементами множества А.

Приведем некоторые формулы алгебры множеств.

7)(А В)∩ А = А - законы поглощения.

(А∩ В) А = А

Доказательство этих формул не представляет трудностей, и основано на непосредственном определении данных операций. На практике данные законы позволяют значительно упрощать формулы алгебры множеств.

§3. Декартово произведение множеств и отношения в множествах

непустое подмножество данного произведения мы будем называть n- арным отношением между элементами множеств Х1,Х2,…,Хn. В случае n = 1 говорят об унарном отношении; при n = 2 –

о бинарном, и так далее….

Пример 2. Пусть X={1,2,…,10}, Y={А,Б,В,Г}.

S={(1,А),(1,Б),(2,Б)}- бинарное отношение между элементами множеств Х и У, а {(2,Г),(В,4)} - не является таковым.

Бинарные отношения занимают особое место, мы изучим некоторые из них.

Пусть Х и У – непустые множества. Будем обозначать ρ - бинарное отношение между элементами множеств Х и У, тогда ρ X ×Y – некоторое множество упорядоченных пар из

X ×Y . Очевидно, можно задать ρ следующим образом: ρ={(x,y)| x X, y Y, P(x,y)}, где P(x,y) – некоторый предикат, заданный на множестве

Пример 3. Определим ρ1={(x, y)x, y N,2x = y } - множество всех упорядоченных пар

натуральных чисел вида (n, 2n).

Если X = Y , то бинарное отношение ρ будем называть бинарным отношением в множестве

элемент множества X. Будем говорить, что ρ(x)– проекция элемента x, если ρ(x)={y Y |(x,y) ρ}. Например, ρ1(n)={2n} при каждом натуральном n.

Пусть A - подмножество X. Проекцией множества А будем называть ρ(A) = U ρ(x). Например

x A

S({1,2}) ={A, Б} , а S({3,4,5}) =

Определение. Пусть ρ – бинарное отношение между элементами множеств X и Y. Будем называть ρ однозначным бинарным отношением, если для произвольного элемента х из множества X, ρ(x) содержит не более одного элемента.

Например, {(1;А),(2А;),(3;Б)} – является однозначным, а {(1;А),(1;Б),(3;В)} – не является однозначным бинарными отношениями.

Заметим, что условие однозначности можно представить следующим образом:

( х,у,z): (x,y) ρ (x,z) ρ y=z.

Определение. Пусть ρ – бинарное отношение между элементами множеств X и Y. Тогда, если выполняются следующие два условия:

1)ρ(x)≠Ø для каждого x X;

2)ρ – однозначное бинарное отношение,

то ρ будем называть отображением множества X в множество Y, или функцией, отображающей множество Х в множество Y. Будем говорить также, что отображение ρ - это отображение «на» Y, если проекция ρ(Х)=Y.

Определение. Пусть ρ – бинарное отношение между элементами множеств X и Y. Будем называть ρ -1 обратным для ρ, если ρ-1 определяется следующим образом: ρ -1={(у,х)/(x,y) ρ }. Очевидно, ρ -1 является при этом отношением между элементами множеств Y и Х. Если и само отношение ρ, и ρ-1 являются однозначными, то ρ называется взаимнооднозначным.

Пример 4. {(x, y) | y = x3 , x R} - это взаимнооднозначное отображение R на R.

называется бинарное отношение между элементами множеств X и Z, которое определяется следующим образом: ρ2 oρ1 X ×Z , ρ2 oρ1 ={(x,z)|( y Y )(x,y) ρ1/\(y,z) ρ2 }.

Если отношения являются функциями, то их произведение называется суперпозицией. Заметим, что для любых бинарных отношений проекция их произведения (ρ2 oρ1)(А)= ρ2(ρ1(А)), тогда не трудно проверить, что суперпозиция двух функций также является функцией, то есть

(( x,y,z Х)((x,y) ε (y,z) ε ) (x,z) ε )).

Приведем некоторые примеры отношений эквивалентности.

1.Обычное отношение равенства в множестве действительных чисел.

2.Отношение подобия в множестве всех треугольников..

3. Можно определить отношение эквивалентности ε в множестве натуральных чисел следующим образом: (x,y) ε , если x и y дают один и тот же остаток при делении на число 7. Договоримся, что принадлежность пары (х,y) ε будем обозначать также хε y и x ~ y.

Теорема. Каждое отношение эквивалентности ε в множестве Х задает разбиение данного множества на непересекающиеся между собой классы эквивалентных между собой элементов (называемых фактор-классами). Обратно, каждое разбиение множества Х на непересекающиеся между собой подмножества определяет отношение эквивалентности в данном множестве Х.

Доказательство. Пусть ε отношение эквивалентности в множестве Х, тогда для каждого x X определим ε(x)= {y X (x, y) ε}- проекцию элемента х.

(x, y) ε (x, z) ε ( y, z) ε , следовательно, все элементы, лежащие в одном таком классе эквивалентны между собой.

первое утверждение теоремы доказано. Обратно, пусть задано некоторое разбиение множества

Приведем еще некоторые понятия теории множеств. Пусть x1 , x2 ,..., xn ,… - бесконечная

последовательность, состоящая из элементов некоторого множества Х. Тогда мы можем данной последовательности поставить в соответствие отображение f: N→X, при этом отображении каждый элемент из N имеет проекцию f (n)= xn . Таким образом можно определить

последовательность, как некоторое индексированное множество {xn }n N , где N - множество

индексов. Аналогично определяется произвольное индексированное множество или

индексированное семейство элементов.

сделать индексированным, например A ={X X }X A , то есть за множество индексов можно взять само множество А, а отображение – тождественное: f (X ) = X .

Для любого множества можно задать некоторую его количественную характеристику. Определение. Если множество Х состоит из конечного числа элементов, то мощностью

множества Х называется количество составляющих его элементов.

Определение. Если между элементами множеств А и В можно установить взаимнооднозначное соответствие ( т.е. существует взаимнооднозначное отображение А на В), то

говорят, что множества А и В имеют одинаковую мощность, или равномощны, и обозначают m(A)= m(B).

Говорят, что мощность множества A не превосходит мощности множества B, если существует подмножество B′ множества B такое, что между элементами множеств A и B′ можно задать взаимнооднозначное соответствие. Будем обозначать это следующим образом:

m(A)≤ m(B). Если одновременно m(A)≤ m(B) и m(B)≤ m(A), то можно показать, что m(A)= m(B).

Множество А, равномощное множеству натуральных чисел N, называют счетным, полагают в этом случае m(A)= χ0 .

Теорема. Объединение счетного семейства счетных множеств является счетным множеством.

Доказательство. Пусть A = {X α }α N - счетное семейство счетных множеств. Тогда, для α N , Xα можно представить в следующем виде: Xα = {xiα }i I . Составим бесконечную таблицу

X1 = {x11 , x12 , x31 ,...x1n ,...},

X 2 = {x12 , x22 , x32 ,...xn2 ,...},

X 3 ={x13 , x23 , x33 ,...xn3 ,...},

......................................

X m = {x1m , x2m , x3m ,...xnm ,...},

.....................................

......................................

состоящую из элементов множеств X1 , X 2 ,…., X m ,…. .

{x11 , x12 , x12 , x13 , x22 , x31 , x14 ,.......}, т.е. мы составляем последовательность, пробегая элементы

нашей таблицы по диагоналям, при этом сдвигаясь в конце каждой на один элемент вправо (или вниз). Таким образом, установленное взаимнооднозначное соответствие между элементами UX α и N доказывает справедливость нашего утверждения.

α N

Будем говорить, что множество А имеет мощность континуума, и обозначать m(A)= C , если А равномощно множеству действительных чисел R. Легко увидеть например, что интервал (0,1) и R равномощны, действительно, функция y = tg(πx −π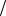2 ) является взаимнооднозначным отображением интервала (0,1) на R, и таким образом, m((0,1))=m(R). Если А подмножество Х, то m(A)≤ m(X ), следовательно m(N )≤ m(R), причём доказано, что m(N )≠ m(R) (χ0 < C). Существует континуум – гипотеза, которая говорит о том, что нет мощностей, промежуточных между χ0 и С.

В завершении данного раздела, рассмотрим ещё одно понятие – отношение порядка, играющее важную роль в теории множеств, и в математике в целом.

Определение. Пусть ρ – бинарное отношение в множестве Х. Будем говорить что ρ –

отношение (частичного) порядка в множестве Х, если выполняются следующие три условия:

1.ρ – рефлексивно, т.е. ∆X ρ;

2.ρ – транзитивно, т.е. ρ2 ρ;

3.ρ – антисимметрично, т.е. ρ∩ρ-1 ∆X .

Если ρ – отношение порядка в Х, то принято обозначать х≤y, если (x,y) ρ. Упорядоченным множеством (X,ρ) ( или (X, ≤)) будем называть множество X с введённым отношением порядка.

Приведём некоторые примеры.

Пример 1. Обычное отношение «меньше, или равно» в множестве всех действительных чисел

– «естественный порядок», таким образом (R, ≤) – упорядоченное множество.

Пример 2. В множестве N – натуральных чисел можно определить отношение (частичного) порядка следующим образом: (x,y) ρ <=> y/x (y является делителем числа х), и) (N, |) - частично упорядоченное множество.

Пример 3. Отношение включёния в множестве всех подмножеств произвольного множества является частичным порядком.

Определение. Отношение (частичного) порядка ρ в множестве X называется линейным

порядком, если для него выполняется дополнительное условие:

4. ρ ρ-1 = X × X .

Последнее означает, что для любых двух элементов x,y X, или (x,y) ρ или (y,x) ρ обязательно (любые два элемента сравнимы).

Если в множестве Х задано отношение (частичного) порядка, то Х называется упорядоченным, если же задано отношение линейного порядка, то – линейно упорядоченным.

Пример 1 – пример линейно упорядоченного множества, примеры 2 и 3 – (частично) упорядоченного.

Определение. Пусть Х (частично) упорядоченное множество, А – подмножество Х. Элемент

а А называется наименьшим (наибольшим) в множестве А, если для х А, а≤х (а≥х,

соответственно). Если каждое непустое подмножество А множества Х обладает наименьшим элементом, то Х называется вполне упорядоченным.

Заметим, что если а – наименьший элемент множества А, то он должен быть сравним с любым элементом данного множества А.

Нетрудно видеть, что (R,≤) из примера 1 не является вполне упорядоченным, например интервал (0,1) не содержит наименьшего элемента, а множество натуральных чисел N с естественным порядком – вполне упорядоченно.

Существуют два равносильных утверждения в теории множеств: первое – теорема Цермело и второе – аксиома выбора.

Приведём их формулировки.

Теорема Цермело. Всякое непустое множество Х можно вполне упорядочить.

Аксиома выбора. Пусть {Хs}s S - произвольное семейство непустых множеств. Тогда найдётся функция, отображающая S в Х= UX s , такая, что для s S: f(s) X s .

s S

§4. Алгебраические структуры

Определение. Пусть Х – непустое множество, X n - его n-я декартова степень. Отображение f

множества X n в множество X называется n-арной операцией в множестве Х.

Например, при n=1, f (x)=x – тождественное отображение Х в себя – унарная операция, при n=2 , f((x,y))=y – бинарная операция в множестве Х, и т.д. ….

К бинарным операциям относятся операции коньюнкции, дизьюнкции, импликации в множестве всех высказываний, а также операции пересечения, объединения, разности множеств в алгебре множеств.

Множество Х введёнными в нём операциями называется алгеброй, или алгебраической структурой. Особенное место среди алгебр занимают бинарные алгебраические структуры.

Пусть f – бинарная операция в множестве Х, тогда f X 2 × X – однозначное бинарное отношение между элементами множеств X 2 и Х. Проекцию (или образ) f(x,y) пары

(x,y) X 2 будем называть результатом операции, и обозначать при помощи некоего знака операции: f(x,y)=x·y или x×y, или x+y, или x • y и т.д…. . Иногда для упрощения обозначения символ “·” опускается, и результат операции записывается в виде xy.

Самые распространённые способы обозначения знака операции – мультипликативный ( · , • ,

×, …) и аддитивный ( + , , +' , …). Если в множестве Х одновременно заданы две операции – то обычно для них применяют аддитивный и мультипликативный способы обозначения “+” и “·”, но не надо их путать с обычными операциями сложения и умножения в множестве R действительных чисел.

Сучётом вышесказанного, будем обозначать (Х , · , + , ×, …) – алгебру с операциями · , + ,

×,… на множестве Х.

Определение. Пусть (Х, · ) и ( X ′, × ) – две бинарные алгебры. Если существует взаимно

Заметим, что с алгебраической точки зрения изоморфные алгебраические структуры можно отождествлять, поскольку операции в них сохраняют соответствие элементов.

Пример 1. Рассмотрим две алгебры (R, + ) и (R+, · ) – действительных и действительных положительных чисел с операциями обычного сложения и умножения действительных чисел. Определим отображения ϕ: R на→R+, полагая ϕ(x)=2х. Тогда ϕ(x+y)=2x+y = 2х · 2y= ϕ(x) · ϕ(y).

Взаимнооднозначность отображения ϕ очевидна, следовательно данные алгебры изоморфны. Определение. Пусть (Х, · ) – бинарная алгебра. Операция “·” называется ассоциативной, если

для любых x,y,z X выполняется равенство (x·y)·z = x·(y·z).

Бинарная алгебра (Х, · ) с ассоциативной операцией называется полугруппой.

Элемент е X называется нейтральным, если для всех х X е·х = х·е=х. Если операция имеет мультипликативное обозначение, то нейтральный элемент называют единичным, и могут обозначать “1”, в случае аддитивной операции – нулевым, и могут обозначать символом “0”.

Заметим, что если нейтральный элемент существует, то он единственный.

Рассмотрим важный пример полугруппы. Пусть Х – произвольное непустое множество. Обозначим FX – множество всех функций, отображающих Х в Х. Тогда ( FX , o) полугруппа, где

o - операция произведения функций. Действительно, если ϕ1, ϕ2, ϕ3 FX , то для любого х Х

( (ϕ3 oϕ2) oϕ 1)(x)=(ϕ3 oϕ2) (ϕ1(x)) =ϕ3(ϕ2 (ϕ1(x))), и (ϕ3( oϕ2 oϕ1))(x)=ϕ3((ϕ2 oϕ1)(x))=ϕ3(ϕ2(ϕ1(x))),

следовательно (ϕ3 oϕ2) oϕ1=ϕ 3 o(ϕ2 oϕ1), и операция “ o“ ассоциативна. Для произвольной полугруппы справедлива следующая

Теорема. В произведении x1 · x2 · … · xn элементов полугруппы скобки можно расставлять в произвольном порядке.

Доказательство. Докажем, что для любого произведения элементов полугруппы (Х, · ) справедливо равенство x1 · x2 · … · xn = x1· (x2· ( … (xn-1 · xn))…). Для n = 3 это верно в силу ассоциативности операции.

Пусть равенство верно для всех n≤k, докажем его справедливость для n = k+1. В этом случае в произведении x1 · x2 · … · xk+1 операция производится k раз, тогда обозначим при помощи скобок

последнее, k-оe применение операции, и запишем x1 · x2 · … · xk+1 = (х1 · … · xi)(xi+1 · … · xk+1), причем i может быть любым от 1 до k. Каждая из этих скобок содержит произведение элементов, состоящее

не более чем из k множителей, а поэтому x1 · x2 · … · xk+1 = (х1 · (x2 ·(…xi))…) · (xi+1 · … · xk+1) =

называется обратным для элемента х, если х x′= x′ x = е.

Если (Х, · ) – полугруппа с единичным элементом, и каждый элемент из Х имеет обратный, то алгебра (Х, · ) называется группой.

Заметим, что если элемент х полугруппы имеет обратный, то он единственен. Действительно,

x′ x x′′ = (x′ x) x′′ = e x′′ = x′′.

В силу этого замечания, обратный элемент для х в случае мультипликативного обозначения операции обозначим х-1.

Понятие группы имеет тесную связь с вопросом о разрешимости уравнения a x = в в произвольной полугруппе.

Следующее утверждение раскрывает эту связь.

Теорема. Полугруппа (Х, · ) является группой тогда и только тогда, когда для любых

а х = а (а−1 в)= (а а−1 ) в = е в = в, аналогично yа = в , и необходимость доказана. Докажем обратное, пусть для a, в Х найдутся x,y X такие, что a x = в и yа = в . Тогда

найдутся ха и yа такие, что a xа = а и yа a = а. Покажем что ха – правый единичный элемент

для (Х, · ), а yа – левый. Действительно, если в- произвольный элемент Х, то существуют x,y X, такие что ах = в и yа = в , но тогда в ха = ( y a) xa = y (a xa ) = y a = в , аналогично и yа в = в. В силу произвольности в Х , отсюда следует, что ха – правый, yа – левый единичный

элемент для всех элементов (Х, · ), а поскольку yа xa = xa , и одновременно yа xa = ya , то ха = yа = е – единичному элементу. Таким образом (Х, · ) – полугруппа с единицей. Покажем, что

yа = в имеют единственное решение (или однозначно разрешимы). Действительно, если ах = в , то a−1 (a x) = a−1 в, и следовательно x = a−1 в, аналогично y = в а−1 .

Замечание 2. Обратный для обратного элемента совпадает с исходным, т.е. (x−1 )−1 = x . Это

следует из единственности обратного для данного элемента в произвольной полугруппе. Замечание 3. Отметим, что для любого элемента х группы (Х, · ) справедливо равенство

(x−1 )n = (xn )−1 для каждого натурального числа n, а тогда, если мы определим x−n = (xn )−1 , то для любых целых чисел n и m выполняются равенства: xnm = (xn )m и xm+n = xm · xn .

Пример 2. Пусть Х = {а}. Определим в Х операцию “·” следующим образом a. a = a . Тогда ({a}, · ) – группа, в которой е = а и а-1 = а.

Пример 3. Множество всех целых чисел Z с операцией обычного сложения: (Z, + ) - является группой. Здесь е=0, а обратный для х – это (– х).

Пример 4. (R\{0}, · ) – множество всех действительных чисел, отличных от нуля, с операцией обычного умножения – является группой. Здесь е = 1, а х-1 совпадает с 1x .

Пример 5. (ФХ , o) – множество всех взаимно однозначных функций, отображающих

Группа (ФХ , o) – называется группой преобразований множества Х.

Заметим, что для мультипликативной операции обратный элемент для элемента х принято

множество Y относительно заданной в X операции “·” является группой, то говорят, что (Y, · ) –

подгруппа группы (Х, · ).

Очевидно, что (Y, · ), где Y X , является подгруппой группы (Х, · ) тогда и только тогда, когда одновременно выполняются два условия: