Lektsii_po_algebre_i_geometrii_Chast1_3

Теперь мы рассмотрим некоторые бинарные алгебры с двумя заданными операциями. Определение. Алгебра (Х, · , + ) с двумя бинарными операциями называется кольцом, если

(Х,+) образует коммутативную группу, (Х, · ) – образует полугруппу и операция умножения “·” является дистрибутивной относительно операции сложения “+“, т.е. выполняются условия:

(x + y) z = x z + y z , и x ( y + z) = x y + x z .

Замечание. Порядок выполнения операций в алгебре (Х, · , + ) определяется с помощью скобок, однако принято считать, что при отсутствии таковых операция “·” имеет приоритетное значение по сравнению с операцией “+“.

Пример 6. Рассмотрим группу ({а}, · ) из примера 2, тогда, если мы определим операцию “+”, в {а}, полагая а + а = а · а, то получим алгебру ({а},+ , · ) – одноэлементное кольцо.

Пример 7. Множество целых чисел, с обычными операциями сложения и умножения (Z, + , · ) – является кольцом.

Пример 7. Положим Kf - множество всех числовых функций из множества Х в R . Определим сумму функций f + g = γ Kf следующим образом: γ(x) = (f+g)(x)= f (x)+g(x); и произведение

функций f · g= λ K f : λ(x) = (f · g)(x)=f(x) · g(x) для каждого x X.

Тогда алгебра (К, + , · ) является кольцом.

Действительно, определим нулевую функцию 0(х)=0 для x X , тогда она является

следовательно (Kf, + ) – коммутативная группа. Ассоциативность операции “·” и дистрибутивность её относительно “+” следуют из свойств сложения и умножения в R.

Определение. Алгебру (P, + , · ) называют полем, если выполняются следующие условия:

1)(P,+, · ) - кольцо.

2)(P\{o},· ) - является коммутативной группой, где 0 – это нейтральный элемент относительно операции “+”. Нейтральный элемент в поле (или кольце) относительно операции “·” обозначают 1 и называют единицей поля (кольца), а 0 – нулём поля (кольца).

Примерами полей могут служить: поле действительных чисел, а также поле (Q ,+, ·) – рациональных чисел. Заметим, что кольцо (Z, + , · ) не является полем.

Приведём некоторые свойства колец и полей.

Пусть (К,+, · ) – произвольное кольцо, тогда справедливы следующие равенства:

1) a · 0=0 · a=0 для а К.

Доказательство. a·0=a·(0+0)=a·0+a·0. Прибавим к обеим частям равенства -(а·0) – обратный для (а·0) по отношению к операции “+”, тогда, используя ассоциативность, получим:0=a·0+0=a·0, аналогично 0·a=(0+0)·a=0·a+0·a, и прибавляя к обеим частям -(0·а) получим 0=0·a+0, и следовательно 0=0·a.

2) -(a·в)=(-a)·в=a(-в) для а, в К.

Доказательство. Докажем, что -(a·в)=(-a)в. Действительно, в силу дистрибутивности (-a)·в+a·в=((-a)+a) ·в=0·в=0 по свойству 1, и следовательно (-a)·в=-(a·в) в силу единственности обратного элемента для a·в. Аналогично доказывается, что –(a ·в)=a ·(-в).

3) Определим разность элементов a-в следующим образом: a-в=a+(-в). Тогда, для а,в,с К справедливо равенство: (a-в)·c=a·c-в·c.

Действительно, (a-в)·c=(a+(-в)) ·c=a·c+(-в)·c=a·c+(-(в·c))=a·c-в·c.

Исключительно важную роль в современной математике играют булевы алгебры. Определение. Бинарная алгебра (В, + , · ) называется булевой алгеброй, если выполняются

следующие условия:

1)Операции “+”, “·” - коммутативны: для a,в B, a+в = в+a, a ·в = в ·a.

2)Операции дистрибутивны относительно друг друга: для a,в,c B (a+в)·c = a·c+в·c,

(a ·в)+c = (a+c)·(в+c).

3)! 0 B такой, что a+0 = a для a B;

! 1 B такой, что a ·1 = a для a B; - условие существования и единственности нулевого и единичного элементов.

4) Для ( a B) ( ! а′ B) такой, что a · а′=0 ; a+ а′ =1 (закон исключённого третьего). Пример 8. Пусть Х – непустое множество. Обозначим 2Х - множество всех подмножеств множества Х. Тогда алгебра (2Х , ,∩) является булевой. Здесь в роли операции “+”

рассматривается операция объединения, а в роли операции “·” – операция пересечения двух множеств. Тогда нулём служит пустое множество, единицей – само множество Х, для каждого

У 2Х ,У′ = Х \ У.

Пример 9. Пусть В – множество всевозможных формул алгебры высказываний. Тогда, отождествляя равносильные формулы, мы получим булеву алгебру (B,V ,&), здесь дизъюнкция

служит операцией сложения “+”, а конъюнкция – операцией умножения “·”, роль нуля играет тождественно ложное, а роль единицы – тождественно истинное высказывания, для формулы А формула A′ совпадает с ¬A .

Более наглядно данную же алгебру представляет следующий пример.

Пример 10. Положим B={a,b}. Определим операции “+” и “·” в {a,b} следующим образом

Тогда ({a,b}, + , · ) – булева алгебра, где 0=а, 1=в, а′=в и в′=а. Определение. Пусть задана булева алгебра

(1)(B, + , · ).

Для данной булевой алгебры мы рассмотрим другую структуру

(2) ( B′, , (·)), где a в = a·в, a(·)в = a+в, и В= В′. Заметим, что алгебра (2) также является булевой алгеброй, она называется двойственной к исходной алгебре (1). Нетрудно

алгебры совпадает с исходной.

Отметим некоторые свойства булевых алгебр.

1.Двойственность. Если справедлива некоторая формула для произвольной булевой алгебры, то будет справедлива и двойственная ей формула, т.е. формула, которая получается из исходной заменой операции “+” на “·”, ”·” на “+”, 0 на 1, и 1 на 0. Данное свойство позволяет удваивать число формул.

2.a·a = a (а+а = а – двойственная) – идемпотентность.

далее, что ( а′+ в′)+(a·в) = а′+( в′+a·в)= а′+( в′+a)·( в′+в) = а′+ в′+a=( а′+a) + в′ = в′+1 = 1, тогда, в силу закона исключения третьего, а′+ в′= (a·в)′.

6.Закон поглощения: a·(a+в) = а , (a+a·в = a).

Доказательство. a·(a+в) = a·a+a·в = a·1+a·в = a· (1+в) = a

7.Склейка: (a+в)·(a+ в′) = a+в· в′= a+0 = a,

(a·в)+(a· в′) = a.

8. ( а′ )′ = а – закон двойного дополнения.

9.0′ =1,

1′ = 0 .

10.a + a′ в = а + в и а (а′+в) = а в – законы частичного поглощения.

§5. Комплексные числа

5.1. Поле комплексных чисел

Рассмотрим R2 = R×R = {(x,y)}|x,y R} - декартов квадрат множества действительных чисел R. Напомним, что упорядоченные пары считаются равными: (x1,y1)=(x2,y2) Ù [(x1=x2) (y1=y2)]. Определим в R2 операцию сложения “+” упорядоченных пар следующим образом:

(x1,y1)+(x2,y2)=(x1+x2,y1+y2).

Эта операция является ассоциативной и коммутативной в силу ассоциативности и коммутативности обычной операции сложения в множестве действительных чисел. Здесь существует нейтральный элемент (0,0)=O. Обозначим R2 = С. Отметим, что для каждого z C существует обратный (относительно операции сложения ”+”): если z = (x,y), то -(x,y) = (-x,-y)

Действительно, (x,y)+(-x,-y)=(0,0)=О. Таким образом (С, + ) – является коммутативной группой.

Введём операцию умножения “·” упорядоченных пар в множестве С полагая

(x1,y1)·(x2,y2) = (x1x2 -y1y2,x1y2+y1x2).

Заметим, что определённая таким образом операция умножения обладает следующими свойствами:

1)Коммутативность: (x1,y1)·(x2,y2)=(x2,y2)·(x1,y1) – следует из свойств умножения действительных чисел;

2)((x1,y1)·(x2,y2))·(x3,y3)=(x1,y1)·((x2,y2)·(x3,y3)) – ассоциативность. Действительно, (z1·z2)·z3 =

(x1x2-y1y2, x1y2+y1x2)·(x3,y3) = (x1x2x3-y1y2x3-x1y2y3-y1x2y3; x1y3x2-y1y2y3+x1y2x3+ y1x2x3) = (x1(x2x3-y2y3)- y1(x2y3+y2x3) = x1(y3x2+y2x3)+y1(x2x3-y2y3)) = (x1y1)(x2x3-y2y3, x2y3+y2x3) = (x1,y1)((x2,y2)(x3,y3))=z1·(z2·z3)

3) (1,0) – нейтральный элемент относительно операции “·”, так как (x,y)·(1,0) = (x,y). Будем обозначать пару (1, 0) = 1

4) Пусть (x,y)≠(0,0) – отличный от нуля элемент С. Тогда существует элемент

группой.

Отметим, что операция умножения в (C, + , · ) дистрибутивна относительно сложения, т.е.

((x1,y1)+(x2,y2))(x3,y3) = (x1,y1)(x3,y3)+(x2,y2)(x3,y3) для xi,yi R, i =1,3 . Действительно:

(x1+x2, y1+y2)(x3,y3) = (x1x3+x2x3-y1y3-y2y3, x1y3+x2y3+y1x3+y2x3)((x1x3-y1y3)+(x2x3-y2y3), (x1y3+y1x3)+ (x2y3+y2x3)) = (x1,y1)(x3,y3)+(x2,y2)(x3,y3).

Значит (C, + , · ) является полем, назовем данную алгебраическую структуру полем комплексных чисел. Покажем, что в этом поле уравнение z2 = -1 имеет решение. Действительно,

Рассмотрим множество действительных чисел R и отображение f : f(x)=(x,0) – множества R на R′. f – является взаимнооднозначным отображением множества R на R′, причём это отображение задаёт соответствие, сохраняющееся при операциях “+” и “·“, т.е., если x -> (x,0), y -> (y,0), то x+y -> (x+y,0), и x·y -> (x·y,0), или f(x+y)=f(x)+f(y)=(x,0)+(y,0), f(x·y)=f(x)·f(y)=(x,0)·(y,0).

Такие соответствия называются изоморфизмами алгебр, и изоморфные алгебраические структуры отождествляются. Следовательно, мы можем считать, что R – подполе C, поскольку R и R′ – изоморфны. При данном изоморфизме паре (а,0) R′ соответствует а R , в частности паре (0,0) соответствует 0.

Любое комплексное число z=(a,b) можно представить следующим образом: z=(a,0)+(в,0)·(0,1). Тогда, отождествляя в силу вышесказанного пару (а,0) с действительным числом а и пару (в,0) с

(a+в·i)+(c+d·i)=(a+c)+(в+d)·i; (a+в·i)·(c+d·i)=(ac-вd)+(ad+вc) ·I . В таком случае, мы получим поле ( C′, + , · ), изоморфное полю (С, + , · ) в силу определения операций в C′.

Запись комплексного числа в алгебраической форме позволяет нам пользоваться всеми свойствами операций + и · в множестве R действительных чисел (коммутативностью, ассоциативностью, дистрибутивностью и т.д.). Таким образом, например, при умножении комплексных чисел в алгебраической форме, мы можем действовать привычным для нас образом:

5.2. Геометрическая интерпретация поля комплексных чисел.

У

М(х,у)

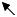γ

О

Х Х

Рассмотрим прямоугольную декартову систему координат на плоскости ХОY. Тогда каждому комплексному числу z = x + y i мы можем поставить в соответствие точку плоскости М(x,y) c

данными координатами. Заметим, что установленное таким образом соответствие между комплексными числами и точками плоскости является взаимнооднозначным. Существует взаимнооднозначное соответствие между точками плоскости и радиус-векторами данных точек

(точке М соответствует вектор ОМ ), и таким образом устанавливается взаимнооднозначное соответствие между комплексными числами и радиус-векторами точек плоскости, соответствующих данным числам. При данном соответствии множеству R действительных чисел соответствует множество точек оси ОХ.

Каждый вектор ОМ характеризуется длинной и направлением. Полагая r – длина вектора, а γ - угол, образуемый данным вектором ОМ с положительным направлением оси ОХ,

(отсчитываемый против часовой стрелки), мы получим полярную систему координат на плоскости, когда каждой точке плоскости М с координатами (х,у) (и, соответственно, радиус-

вектору ОМ данной точки), соответствует упорядоченная пара действительных чисел ( r,γ ), причем декартовы координаты точки связаны с полярными следующим образом: x = r cosγ , y = r sinγ .

5.3. Действия над комплексными числами в тригонометрической форме

Пусть z1 = x1+i·y1= r1· (cosγ1 + i ·sinγ1 ); z2 = x2+i·y2= r2· (cosγ2 + i ·sinγ2 ).

Тогда z1·z2=r1·r2(cosγ1·cosγ2+i·(sinγ2·cosγ1+cosγ2·sinγ1)+i·i·sinγ1sinγ2)=r1·r2(cos(γ1+γ2)+i·sin(γ1+γ2)).

Таким образом, при умножении двух комплексных чисел в тригонометрической форме, их модули перемножаются, а аргументы складываются. Данное свойство распространяется на произведение любого конечного числа комплексных чисел, и позволяет легко находить степень комплексного

тригонометрической форме, модуль первого делится на модуль второго, а аргумент второго вычитается из аргумента первого.

Действительно, заметим, что (n z)k=n =(n z)k=0 , (n z )k =n+1 =(n z )k =1 ,…, (n z )k =2 n−1 =(n z )k =n−1 , и т.д.

Таким образом, придавая k значения от 0 до n-1, мы получим n различных корней, которые геометрически будут лежать на окружности радиуса r′ = n r , и отличаться каждый от соседнего

на угол 2nπ . При всех остальных целых k мы будем попадать в эти уже построенные точки.

5.4. Комплексно-сопряженные числа

Если z = x + y i – комплексное число, то число z = x − y i =x называют сопряжённым

для z.

Отметим некоторые свойства сопряжённых чисел:

1)z = z ;

2)комплексные числа z и z расположены симметрично относительно оси ОХ;

3)arg z = −arg z ;

4)z z = z 2 ;

5)z1 ± z2 = z1 ± z2 ;

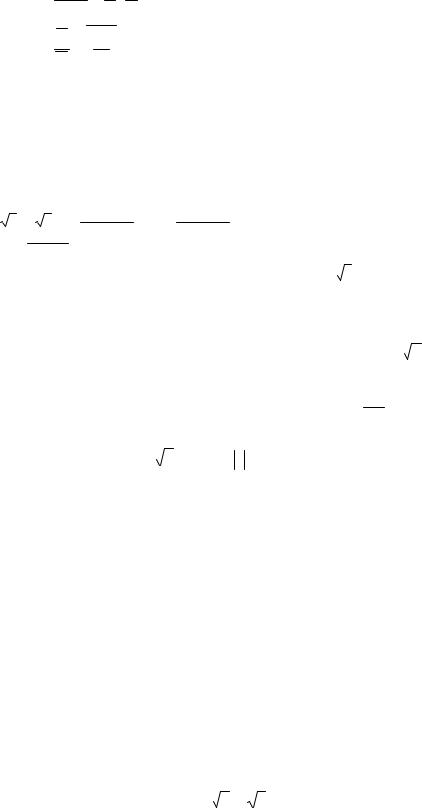
6)z1 z2 = z1 z2 ;

7)z1 = z1 . z2 z2

Доказательство данных свойств не представляет затруднений и носит технический характер.

5.5. Корни из единицы

Поскольку

1 =1(cos0 +isin 0) , то для любого n N

Заметим, что данные корни лежат на окружности единичного радиуса и делят её на п равных частей. Отсюда следует, что все эти корни можно разбить на пары сопряжённых чисел.

Отметим также, что для любого комплексного числа z все его корни n-ой степени могут быть получены при умножении любого одного из его корней z′ = n z на все корни n-й степени из единицы: ε1,...,εn . Действительно, из вышесказанного следует, что корни из единицы ε1,...,εn

лежат на окружности единичного радиуса через угол 2nπ , и, следовательно, произведение

выбранного корня z′ на них также даст нам такое же расположение полученных чисел, только на окружности радиусом n r , где r = z . Таким образом, мы получаем п различных комплексных

чисел. Заметим, что все эти произведения являются корнями п-й степени из z, поскольку

(z′ ε j )n = (z′)n ε nj = z 1 = z .

Отметим, что все корни п-й степени из z, также как и корни из единицы, разбиваются на пары сопряжённых чисел.

5.6. Показательная форма комплексного числа.

Рассмотрим комплексное число z в тригонометрической форме z = r (cosγ + i sin γ ) и

обозначим еiγ = (cosγ + i sin γ ). Тогда число z можно записать в виде: z = rеiγ , данный вид

называется показательной формой комплексного числа z. Исходя из свойств операций умножения и деления комплексных чисел в тригонометрической форме, мы получим справедливость

функции. Отметим также, что корни из комплексного числа z в показательной форме имеют вид:

γ +2πк

n z = n r е n , где k=0,…,n-1.

ГЛАВА 2

СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ.

§6. Определители и их свойства.

a11 x + a12 y + a13 z = c1a 21 x + a 21 y + a 23 z = c 2a31 x + a 32 y + a33 z = c3

Пусть ∆ = A ≠ 0 , тогда данная система имеет единственное решение, которое находится по

формулам:

x = ∆∆1 , y = ∆∆2 , z = ∆∆3 ,

Где ∆i получается из определителя ∆ путём замены i-го столбика на столбик из свободных членов с1,с2,с3, i =1,3 . Данное утверждение будет нами доказано в дальнейшем.

6.2. Определитель n-го порядка.

Рассмотрим множество P первых n натуральных чисел: P = {1,2,..., n}. Если все эти числа записать в определенном порядке так, чтобы они не повторялись, то получим упорядоченную n – ку, являющейся элементом n – ой декартовой степени множества P, например (1,2,..,n) Pn - упорядоченная n-ка, причём напомним, что, например, (2,1,..., n) ≠ (1,2,..., n) .

Любая такая упорядоченная n-ка будет называется перестановкой.

Выясним сколько всего перестановок из элементов Р существует: на первом месте может быть любое из n чисел, на втором (при выбранном первом) – любое из оставшихся n-1 и т.д. Таким образом, количество всех различных вариантов выбора элементов составляет произведение n!=1·2 ….. (n-1)·n (n факториал), следовательно, количество всех возможных перестановок первых n чисел равно n!

Рассмотрим произвольную перестановку (α1, α2, … , αn). Будем говорить, что пара (αi, αj) образует инверсию, если i < j , но αi > αj. Будем говорить, что перестановка четная, если в ней содержится четное число инверсий, и нечетная в противном случае.

Транспозицией будем называть перемену местами двух элементов перестановки.

Теорема. Одна транспозиция меняет чётность перестановки.

Доказательство. Рассмотрим перестановку (α1, … ,αi, … , αj, … , αn). Совершим транспозицию двух элементов: поменяем местами αi и αj. Если эти элементы соседние, то утверждение следует из того, что инверсии выбранных элементов с остальными элементами остаются такими же, а расположение их относительно друг друга меняется.

Пусть ј = і+ĸ, и ĸ≠1.

После транспозиции элементов αi и αj мы получим перестановку (α1,… ,αj,… , αi,,… , αn). Здесь, все оставшиеся элементы (кроме αi и αj) будут составлять между собой те же инверсии, что и раньше. Данную перестановку можно также получить следующим образом: в исходной

Таким образом, требуемую перестановку можно получить, совершив (2k - 1) транспозиций соседних элементов. Полученная перестановка, следовательно, имеет другую четность, нежели исходная, и предложение доказано.

где (α1, … , αn) - любая перестановка элементов из множества Р, а (φ(α1),…, φ(αn)) – тоже перестановка, состоящая из образов элементов верхней перестановки при данном отображении φ, причем βi = ϕ(i) при всех i =1,2,…,n.

Подстановка называется четной, если четности верхней и нижней перестановок, образующих ее, совпадают, и нечетной в противном случае. Подстановку вида (*) очевидно можно привести за конечное число транспозиций одновременно верхних и нижних соответствующих друг другу элементов к каноническому виду (1). Четности подстановок (*) и (1) совпадают, поскольку каждая такая транспозиция меняет одновременно четность верхней и нижней перестановок, составляющих подстановку, поэтому данное определение четности и нечетности подстановки является корректным.

Заметим, что множество всех подстановок n-ой степени образует группу преобразований множества P, а все четные подстановки в ней образуют подгруппу.

Определение. Прямоугольную таблицу, состоящую из n-строк и m-столбцов, элементами которой являются элементы некоторого поля Р, мы будем называть матрицей размерности n×m на полем Р.

Каждый элемент аіј матрицы А имеет два индекса: первый индекс указывает номер строки, а второй - номер столбца, в котором находится данный элемент. Будем данную матрицу А обозначать также:

А=(аіј)n×m, и А=[аіј]n×m.

Замечание. В дальнейшем мы рассматриваем матрицы и определители над полем действительных чисел, но все рассуждения и результаты без ограниченной общности переносятся на случай любого другого поля.

Если число строк и столбцов матрицы А совпадает и равно n, то матрица А называется

квадратной матрицей n-ого порядка.

Определение. Пусть матрица А – это квадратная матрица n-ого порядка. Определителем матрицы А называется сумма всевозможных произведений элементов матрицы А, стоящих в различных строках и столбцах, взятых со знаком “+” или “-” в зависимости от четности подстановки, образуемой индексами элементов произведения.

Данное определение справедливо и для определителя 1-ого порядка. Таким образом, обозначая определитель матрицы А как |А|, получим, что

A = ∑(−1)δ a1α1 a2α2 ... anαn ,

где δ=1, если перестановка (α1, …, αn) – нечетная, и δ=0, если перестановка (α1, . . .,αn)- четная. Каждое слагаемое указанной суммы мы будем называть членом определителя |А|. Заметим, что число различных членов определителя равно n!.

6.3. Свойства определителей.

Свойство 1. Если в определителе существует строчка (столбец) состоящая из одних нулей, то данный определитель равен нулю.

Определение. Матрица А'= (aij′ )m×n называется транспонированной матрицей для матрицы

А=(аіј)n×m и обозначается Ат, если для любых индексов і=1,m и ј=1,n выполняется условие а'іј=

ајі.

Столбцами матрицы А' являются соответствующие строки матрицы А, а строчками матрицы А' – соответствующие столбцы матрицы А.

Заметим, что (Ат)т = А.

Свойство 2. При транспонировании матрицы её определитель не меняется.