§8 Частотные характеристики линейных систем

При подаче на вход линейного звена гармонического воздействия на выходе этого звена в установившемся режиме также будет получена гармоническая функция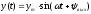той же частоты, но отличающаяся от входной по амплитуде и по фазе (рис. 8.1)

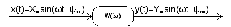
Рисунок 8.1 Гармонические сигналы

Изменения амплитуды и фазы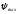зависит как от свойств самого звена, так и от угловой частотывходного воздействия.

Отношение выходной величины звена (системы) к входной, выраженных в комплексной форме, называется комплексной частотной характеристикой (КЧХ) или амплитудно-фазовой частотной характеристикой (АФЧХ или АФХ).

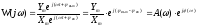(1)

где:

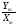=- модуль КЧХ;

- аргумент КЧХ.

Как видно из (1) КЧХ не зависит от времени, в этом ее принципиальное отличие от временных характеристик. Если временные характеристики определяют поведение звена в переходном процессе, то КЧХ выражает зависимость параметров установившихся выходных колебаний от тех же параметров входных колебаний при различных угловых частотах .

КЧХ полностью определяет и динамические свойства системы, подобно временным характеристикам и ДУ.

Для получения КЧХ достаточно в передаточной функции W(p) заменить комплексную переменнуюpна.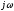

Зависимость отношения амплитуды выходной величины к амплитуде входной величины от угловой частоты называется амплитудно-частотной характеристикой (АЧХ).

А==А()

АЧХ показывает, что линейный элемент или система изменяет амплитуду гармонического сигнала: амплитуда уменьшается или увеличивается в А раз при изменении частоты.

АЧХ является модулем КЧХ.

А()=

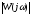
Зависимость сдвига по фазе выходного сигнала относительно входного от угловой частоты называется фазочастотной характеристикой (ФЧХ):

ФЧХ показывает, что линейное звено или система изменяет фазу гармонического сигнала: сдвиг по фазе увеличивается или уменьшается на градусов (или радиан).

ФЧХ является аргументом КЧХ.

=argW()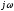

Частотные характеристики линейного звена (системы) зависят только от свойств этого звена и не зависят от амплитуды и фазы входных гармонических сигналов.

Частотные характеристики связаны между собой соотношением:

Функция при каждом значении частотыявляется комплексной величиной и поэтому может быть представлена в алгебраической форме:

=U()+jV()

где U() – вещественная частотная характеристика (ВЧХ);

V() – мнимая частотная характеристика (МЧХ).

Годограф вектора 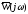при изменении частотыот 0 доназываетсяамплитудно-фазовой характеристикой (АФХ).

Ее строят на комплексной плоскости. По оси абсцисс откладывают величину U(), а по оси ординатV().

На рисунке 8.2 представлены типовые КЧХ, АЧХ и ФЧХ системы:

ω

ω=∞

ω=0

W(ω₁)

φ(ω₁)

V(ω₁)

A(ω₁)

U(ω)

jV(ω)

A(ω)

A_max

A(0)=1

0,707A(0)

ω_р

ω_ср

ω₀

ω

АЧХ

ФЧХ

ω

φ(ω)

Рис. 8.2 Частотные характеристики системы

Между частотными характеристиками имеются следующие очевидные соотношения:

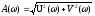
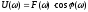
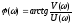
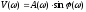
§9 Типовые звенья линейных систем и их динамические характеристики

Типовым элементарным динамическим звеном называется звено, динамика которого описывается диффернциальным уравнением не выше второго порядка.

Типовые звенья классифицируются в зависимости от вида дифференциального уравнения на позиционные, интегрирующие, дифференцирующие, запаздывания.

Позиционными называются звенья в левой части дифференциального уравнения которых выходная величина и её производные, а в правой – входная величина.