КСГПСЧ (Одоев 24 группа)

Министерство образования и науки Российской Федерации

федеральное государственное автономное образовательное учреждение

высшего профессионального образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Кафедра информационной безопасности

(наименование кафедры)

Одоев Кирилл Александрович

(фамилия, имя, отчество студента)

Институт

ИМИКТ

курс

2

группа

317314

090900.62 Информационная безопасность (код и наименование направления подготовки/специальности)

КУРСОВАЯ РАБОТА

По дисциплине

Теоретические основы компьютерной безопасности

На тему

Криптографически стойкие генераторы псевдослучайных последовательностей

(наименование темы)

________________________________________________________________________________________________________________________________________

Работа допущена к защите

(подпись руководителя)

(дата)

Признать, что работа

выполнена и защищена с оценкой

Руководитель

(должность)

(подпись)

(инициалы, фамилия)

(дата)

Архангельск 2015

Министерство образования и науки Российской Федерации

федеральное государственное автономное образовательное учреждение

высшего профессионального образования «Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Кафедра прикладной информатики и информатизации образования

(наименование кафедры)

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ

ппо

Теоретическим основам компьютерной безопасности

(наименование дисциплины)

студенту

ИМИКТ

института

2

курса

317314

группы

Одоеву Кириллу Александровичу

(фамилия, имя, отчество студента)

090900.62 Информационная безопасность (код и наименование направления подготовки/специальности)

ТЕМА:

Криптографически стойкие генераторы псевдослучайных

последовательностей

ИСХОДНЫЕ ДАННЫЕ:

Что такое случайные и псевдослучайные

последовательности и их генераторы, тестирование случайных и

псевдослучайных последовательностей, какие генераторы можно назвать

криптографически стойкими.

Срок выполнения: с

«

»

20 г. по

«

»

20 г.

Руководитель работы

(должность)

(подпись)

(инициалы, фамилия)

Архангельск 2015

Лист замечаний

Оглавление

КУРСОВАЯ РАБОТА 1

ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ 2

Лист замечаний 3

Введение 5

Заключение 19

Список использованной литературы: 20

ВВЕДЕНИЕ 5

1.Случайные и псевдослучайные последовательности 6

2.1. Генераторы случайных и псевдослучаныx последовательностей 6

2.2. Классификация алгоритмов генерации 9

3.1. Криптографичекси стойкие генераторы псевдослучайных чисел 10

3.2. Статистические тесты на случайность 11

3.3. Тест на следующий бит 12

4. Реализации КСГПСЧ 13

4.1. Реализации на основе криптографических алгоритмов 13

4.2. Реализации на основе математических задач 14

4.3. Специальные реализации 16

ЗАКЛЮЧЕНИЕ 18

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 19

Введение

Цель работы: определить что такое случайные и псевдослучайные последовательности , что из себя представляют генераторы таких последовательностей, и какие из них можно назвать криптографически стойкими.

Задачи: 1.Дать определение случайным и псевдослучайным последовательностям. 2.Рассмотреть , что такое генератор псевдослучайных последовательностей

3.Рассмотреть критерии , по которым подобные генераторы могут называться криптографически устойчивыми.

Случайные числа и их генераторы являются неотъемлемыми элементами современных криптосистем. Современная информатика широко использует псевдослучайные числа в самых разных приложениях — от метода Монте-Карло и имитационного моделирования до криптографии. При этом от качества используемых генераторов псевдослучайных чисел (далее ГПСЧ) напрямую зависит качество получаемых результатов. Это обстоятельство подчёркивает известный афоризм математика Роберта Кавью: «генерация случайных чисел слишком важна, чтобы оставлять её на волю случая».

СЛУЧАЙНЫЕ И ПСЕВДОСЛУЧАЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Для начала дадим определение случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Однако в программировании принято говорить не о случайных а псевдослучайных величинах. Почему? Приведем пример.

Допустим, надо получить последовательность случайных чисел n₁, n₂, … n_i на определенном отрезке, например от 0 до 1. Можно взять некоторый коэффициент K, имеющий достаточно большое значение, и первое любое число (n₁), принадлежащее заданному отрезку. Последующее число (n₂) можно получать, умножая K на n₁ и отбрасывая целую часть; получить n₃ можно умножив K на полученное ранее n₂ и т.д. В результате из-за хаотичности результатов будет казаться, что полученные значения случайны. На самом деле это не так, т.к. получаемые значения всегда можно вычислить, зная n₁ и K. Хотя реальные алгоритмы случайных чисел несколько сложнее, но все равно «случайность» получается предопределенной. При использовании же ЭВМ следует помнить , что компьютер изначально детерминирован и работает по определенным алгоритма , а значит в «случайности» используемых параметров можно усомниться. Поэтому в программировании используется понятие псевдослучайных чисел, а не случайных.

Псевдослучайная последовательность (ПСП) — последовательность чисел, которая была вычислена по некоторому определённому арифметическому правилу, но имеет все свойства случайной последовательности чисел в рамках решаемой задачи.

ГЕНЕРАТОРЫ СЛУЧАЙНЫХ И ПСЕВДОСЛУЧАНЫX ПОСЛЕДОВАТЕЛЬНОСТЕЙ

Источники настоящих случайных чисел найти крайне трудно. Физические шумы, такие как детекторы событий ионизирующей радиации, дробовой шум в резисторе или космическое излучение, могут быть такими источниками. Однако применяются такие устройства в приложениях сетевой безопасности редко. Сложности также вызывают грубые атаки на подобные устройства.

Криптографические приложения используют для генерации случайных чисел особенные алгоритмы. Эти алгоритмы заранее определены и, следовательно, генерируют последовательность чисел, которая теоретически не может быть статистически случайной. В то же время, если выбрать хороший алгоритм, полученная численная последовательность будет проходить большинство тестов на случайность.

Альтернативным решением является создание набора из большого количества случайных чисел и опубликование его в некотором словаре, называемом «одноразовым блокнотом». Тем не менее, и такие наборы обеспечивают очень ограниченный источник чисел по сравнению с тем количеством, которое требуется приложениям сетевой безопасности. Хотя данные наборы действительно обеспечивают статистическую случайность, они недостаточно безопасны, так как злоумышленник может получить копию словаря.

Для некоторых криптографических применений необходимы массивы случайных чисел , которые по своему назначению требуют конфиденциального использования. Генерация же случайных чисел на компьютерах весьма затруднительна. Известно, что проблема генерации случайной последовательности с произвольным законом распределения вероятностей сводиться к проблеме генерации так называемой равномерно распределенной случайной величины (РРСП), или, как ее часто называют в криптографических приложениях, «чисто случайной» последовательности. РРСП – это случайная последовательность 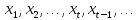со значениями в дискретном множе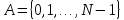стве , определенная на вероятностном пространстве 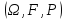и удовлетворяющая двум свойствам: