КСГПСЧ (Одоев 24 группа)

Свойство 1. Для любого 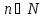и произвольных значений индексов 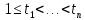случайные величины 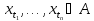независимы в совокупности.

Свойство 2. Для любого номера 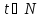случайная величина 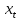имеет дискретное равномерное на 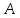распределение вероятностей:

Из базовых свойств 1 и 2 вытекают следующие дополнительные свойства, используемые при генерации случайных чисел.

Свойство 3. Если 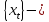РРСП , то для любого 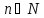и любой фиксированной последовательности индексов n-мерное дискретное распределение вероятностей вектора (слова) 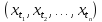является равномерным:

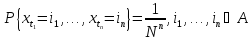
Свойство 4. Если 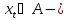элемент РРСП, то справедливы следующие выражения его начального и центрального моментов k-го порядка:

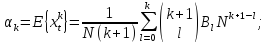
где 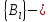числа Бернулли.

Свойство 5. Для ковариационной функции и спектральной плотности РРСП справедливы следующие выражения:

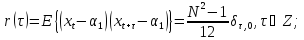
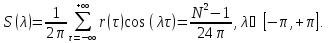
Свойство 6 (воспроизводимость при прореживании). Для любой фиксированной последовательности моментов времени 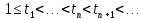при «прореживании» РРСП 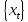возникает последовательность

которая также является РРСП.

Свойство 7 (воспроизводимость при суммировании). Если 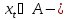РРСП, а 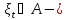произвольная неслучайная либо случайная последовательность, не зависящая от , то случайная последовательность

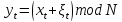
также является РРСП.

Свойство 8. Если РРСП, то количество информации по Шеннону, содержащейся в отрезке последовательности 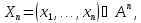о будущем элементе 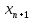равному нулю:

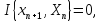
поэтому для любого алгоритма прогнозирования 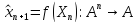вероятность ошибки прогнозирования не может быть меньше , чем для «угадывания по жребию»:

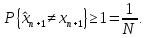
Свойство 9. Если 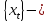РРСП, то для любого 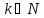и произвольно интегрируемой борелевской функции k переменных 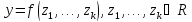, при 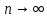имеет место сходимость «почти наверное»:

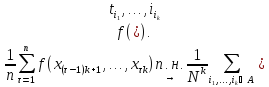
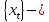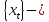Свойство 10. Если равномерно распределенная последовательность порядка в смысле Г.Вейля, то РРСП.

С учетом этих свойств определим понятие генератора случайной последовательности:

Генератор РРСП – устройство , позволяющее по запросу получить реализацию равномерно распределенной случайной последовательности 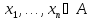длиной 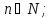элементы 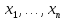этой реализации принято называть случайными числами. Существует три типа генераторов РРСП: 1) табличный, 2) физический, 3) программный. Далее будут рассматриваться именно программные генераторы.

Программный генератор РРСП – программа имитации на компьютере реализации РРСП. Имитируемая последовательность 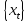называется псевдослучайной, так как она вычисляется на компьютере по известному детерминированному (обычно рекуррентному) соотношению, и в то же время ее статистические свойства «близки» (по определенным критериям) к свойствам РРСП. По другому он еще называется генератором псевдослучайных чисел (ГПСЧ).

КЛАССИФИКАЦИЯ АЛГОРИТМОВ ГЕНЕРАЦИИ

Классификация существующих алгоритмов генерации псевдослучайных последовательностей представлена на рис.2.1. Выделяют три основных подхода к построению алгоритмов генерации: 1) прямые методы построения элементарных рекуррентных последовательностей:

проходящих статистические тесты; 2) методы улучшения элементарных последовательностей, заключающиеся в специальных функциональных преобразованиях этих последовательностей для уменьшения отклонения их статистических свойств РРСП; 3) комбинирование алгоритмов генерации, построенных с помощью первого или второго подхода.

Рис.1. Классификация алгоритмов генерации псевдослучайных последовательностей

КРИПТОГРАФИЧЕКСИ СТОЙКИЕ ГЕНЕРАТОРЫ ПСЕВДОСЛУЧАЙНЫХ ЧИСЕЛ

Криптографически стойкий генератор псевдослучайных чисел (далее КСГПСЧ)- это ГПСЧ с определёнными свойствами, позволяющими использовать его в криптографии.

Многие прикладные задачи криптографии требуют случайных чисел, например:

- генерация ключей

- одноразовые случайные числа

- одноразовые шифроблокноты

- соль (модификатор) в схемах цифровой подписи

и т.д.

Требуемое «качество» случайности варьируется от задачи к задаче. В идеале, генерация случайных чисел в КСГПСЧ использует высоконадёжный источник энтропии (меры неопределенности , непредсказуемости информации), которым может быть аппаратный генератор случайных чисел или ход непредсказуемых процессов в системе. С точки зрения теории информации количество случайности — энтропия, которая может быть получена, равна энтропии, предоставляемой системой. Но зачастую в реальных ситуация требуется больше случайных чисел, чем можно получить при существующей энтропии. К тому же процедура получения случайности из самой системы требует достаточно много ресурсов (памяти и времени). В таких случаях, оправданно использование КСГПСЧ — это позволяет «растянуть» имеющуюся энтропию на большее число бит.

Требования к обычному генератору псевдослучайных чисел выполняются и криптографически стойким ГПСЧ, обратное неверно. Требования к КСГПСЧ можно разделить на три группы:

- он должен проходить статистические тесты на случайность;

- он должен удовлетворять «тесту на следующий бит»;

- КСГПСЧ должен оставаться надёжным даже в случае, когда часть или все его состояния стали известны (или были корректно вычислены).

Большинство генераторов псевдослучайных чисел не подходят для использования в качестве КСГПСЧ по 2 и 3 киртерию. Во-первых, несмотря на то, что многие ГПСЧ выдают последовательность случайную с точки зрения разнообразных статистических тестов, они не надёжны по отношению к обратной разработке. Могут быть обнаружены специализированные, особым образом настроенные тесты, которые покажут, что случайные числа, получаемые из ГПСЧ не являются по настоящему случайными. Во-вторых, для большинства ГПСЧ возможно вычислить всю псевдослучайную последовательность, если их состояние скомпрометировано, что позволит криптоаналитику получить доступ не только к будущим сообщениям, но и ко всем предыдущим. КСГПСЧ разрабатываются с учётом сопротивляемости к различным видам криптоанализа.

СТАТИСТИЧЕСКИЕ ТЕСТЫ НА СЛУЧАЙНОСТЬ

В современных криптосистемах интенсивно используются равномерно распределенные случайные последовательности или имитирующие их псевдослучайные последовательности. При этом стойкость подобных криптосистем существенно зависит от того, насколько точно соответствует модели РРСП используемая последовательность 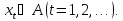Проверка близости 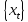к модели РРСП осуществляется методами статистического тестирования и состоит в проверке выполнения базовых свойств 1 и 2 РРСП. Иногда вместо базовых свойств 1 и 2 проверяют выполнение свойств 3-10 РРСП, следующих из 1 и 2.

Наиболее известной является так называемая «батарея статистических тестов» Дж.Марсальи, предложенная им в 1985 г. и реализованная в пакете статистических эмпирических тестов «TestU01» на языке ANSI C в 1996 г. Другое название тестов - тесты diehard.

Всего в этот сборник включено 12 тестов:

1) Дни рождения (Birthday Spacings) — выбираются случайные точки на большом интервале. Расстояния между точками должны быть асимптотически распределены по Пуассону. Название этот тест получил на основе парадокса дней рождения.

2) Пересекающиеся перестановки (Overlapping Permutations) — анализируются последовательности пяти последовательных случайных чисел. 120 возможных перестановок должны получаться со статистически эквивалентной вероятностью.

3) Ранги матриц (Ranks of matrices) — выбираются некоторое количество бит из некоторого количества случайных чисел для формирования матрицы над {0,1}, затем определяется ранг матрицы. Считаются ранги.

4) Обезьяньи тесты (Monkey Tests) — последовательности некоторого количества бит интерпретируются как слова. Считаются пересекающиеся слова в потоке. Количество «слов», которые не появляются, должны удовлетворять известному распределению. Название этот тест получил на основе теоремы о бесконечном количестве обезьян.

5) Подсчёт единичек (Count the 1’s) — считаются единичные биты в каждом из последующих или выбранных байт. Эти счётчики преобразуется в «буквы», и считаются случаи пятибуквенных «слов».

6) Тест на парковку (Parking Lot Test) — единичные окружности случайно размещаются в квадрате 100×100. Если окружность пересекает уже существующую, попытаться ещё. После 12 000 попыток, количество успешно «припаркованных» окружностей должно быть нормально распределено.

7) Тест на минимальное расстояние (Minimum Distance Test) — 8000 точек случайно размещаются в квадрате 10 000×10 000, затем находится минимальное расстояние между любыми парами. Квадрат этого расстояния должен быть экспоненциально распределён с некоторой медианой.

8) Тест случайных сфер (Random Spheres Test) — случайно выбираются 4000 точек в кубе с ребром 1000. В каждой точке помещается сфера, чей радиус является минимальным расстоянием до другой точки. Минимальный объём сферы должен быть экспоненциально распределён с некоторой медианой.

9) Тест сжатия (The Squeeze Test) — 231 умножается на случайные вещественные числа в диапазоне [0,1) до тех пор, пока не получится 1. Повторяется 100 000 раз. Количество вещественных чисел необходимых для достижения 1 должно быть распределено определённым образом.

10) Тест пересекающихся сумм (Overlapping Sums Test) — генерируется длинная последовательность вещественных чисел из интервала [0,1). В ней суммируются каждые 100 последовательных чисел. Суммы должны быть нормально распределены с характерными средним и дисперсией.

11) Тест последовательностей (Runs Test) — генерируется длинная последовательность на [0,1). Подсчитываются восходящие и нисходящие последовательности. Числа должны удовлетворять некоторому распределению.

12) Тест игры в кости (The Craps Test) — играется 200 000 игр в кости, подсчитываются победы и количество бросков в каждой игре. Каждое число должно удовлетворять некоторому распределению.

ТЕСТ НА СЛЕДУЮЩИЙ БИТ

Тест, служащий для проверки генераторов псевдо-случайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые 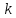битов случайной последовательности, сможет предсказать 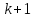бит с вероятностью, неравной .

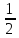В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило для этой цели используются различные статистические тесты, такие как например тесты DIEHARD или тесты NIST. Эндрю Яо доказал в 1982 году что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.

Двоичный генератор проходит тест на следующий бит, если:

Для любого 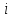и любого вероятностного полиномиального по времени алгоритма 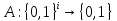(Алгоритм, имеющий в качестве начальных данных последовательность битов длиной i, и выдающий на своём выходе бит), выполняется следующее неравенство:

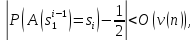
где 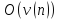- обозначение функции, убывающей быстрее чем обратный полином степени n.

Хоть тест на следующий бит и является универсальным методом проверки независимости выходных бит последовательности, он пригоден лишь для несмещенных последовательностей, то есть таких, в которых вероятность появления единицы эквивалентна вероятности появления нуля.

Если же выходная последовательность должна заведомо обладать некоторым смещением, то данный тест не пригоден. Поэтому для тестирования независимости выходных бит таких последовательностей приходится использовать другие тесты. В частности было предложено расширение теста на следующий бит - сравнительный тест на следующий бит. Идея теста заключается в том, что мы изначально полагаем, что распределение выходной последовательности описывается некоторой математической моделью, а тест служит для проверки соответствия генератора этой модели.

РЕАЛИЗАЦИИ КСГПСЧ

Существует три класса реализации КСГПСЧ:

- на основе криптографических алгоритмов

- на основе вычислительно сложных математических задач

- специальные реализации

В последних часто используются дополнительные источники энтропии, поэтому, строго говоря, они не являются «чистыми» генераторами, так как их выход не полностью определяется исходным состоянием. Это позволяет дополнительно защититься от атак, направленных на определение исходного состояния.

РЕАЛИЗАЦИИ НА ОСНОВЕ КРИПТОГРАФИЧЕСКИХ АЛГОРИТМОВ

1) Безопасный блочный шифр можно преобразовать в КСГПСЧ запустив его в режиме счетчика. Таким образом, выбрав случайный ключ, можно получать следующий случайный блок применяя алгоритм к последовательным натуральным числам. Счет можно начинать с произвольного натурального числа. Период будет не больше чем для -битного блочного шифра. Естественно безопасность такой схемы полностью зависит от секретности ключа.

2) Криптографически стойкая хеш-функция также может быть преобразована в КСГПСЧ. В таком случае исходное значение счетчика должно оставаться в секрете. Однако, некоторые авторы предостерегают от такого использования хеш-функций.

3) Большинство потоковых шифров работают на основе генерации псевдослучайного потока бит, которые некоторым образом комбинируется (почти всегда с помощью операции XOR) с битами открытого текста. Запуск такого шифра на последовательности натуральных чисел даст новую псевдослучайную последовательность, возможно, даже с более длинным периодом. Такой метод безопасен только если в самом потоковом шифре используется надёжный КСГПСЧ (что не всегда так). Опять же, начальное состояние счётчика должно оставаться секретным.

Наиболее яркими примерами подобных генераторов являются AES, ГОСТ 28147-89.

Алгоритм ГОСТ 28147-89

ГОСТ – это блочный алгоритм, разработанный в Советском Союзе. Он представляет собой 64-битовый алгоритм с 256-битовым ключом. Кроме того, в ГОСТе применяется добавочный ключ. В процессе работы алгоритма последовательно, на 32 раундах, выполняется простой алгоритм шифрования.

Вначале шифруемый текст разбивается на левую и правую половины. На раунде 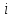используется подключ 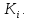На каждом -ом раунде алгоритма выполняются следующие операции:

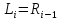
Функция 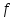проста. Сначала над правой половиной шифруемого текста и -ым подключом выполняется операция сложения по модулю . Результат операции разбивается на восемь 4-битовых фрагмента; каждый из этих фрагментов поступает на вход своего -блока. В алгоритме используются восемь различных 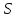-блоков. Каждый из 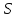-блоков является перестановкой чисел от 0 до 15. Все 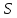-блоки различны, фактически они служат дополнительным ключевым материалом и должны храниться в секрете.

Рис.2. Раунд алгоритма ГОСТ

Выходы всех восьми -блоков объединяются в одно 32-х битовое слово; затем все это слово сдвигается циклически влево на 11 битов. На завершающем этапе результат объединяется операцией XOR с левой половиной шифруемого текста, создавая новую правую половину, а правая половина становиться новой левой половиной. После выполнения операций 32 раза все будет завершено.

Подключи генерируются так. Ключ размером 256 битов разбивается на восемь 32-битовых блоков: 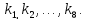На каждом раунде используется свой подключ. Расшифровывание выполняется точно также, как зашифрование, инвертируется порядок подключей

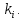
РЕАЛИЗАЦИИ НА ОСНОВЕ МАТЕМАТИЧЕСКИХ ЗАДАЧ

1) Алгоритм Блюма — Блюма — Шуба имеет высокую криптостойкость, основанную на предполагаемой сложности факторизации целых чисел. Однако, этот алгоритм отличается очень медленной работой.

2) Алгоритм Блюма — Микали основан на задаче дискретного логарифма.

Алгоритм BBS (Blum-Blum-Shub)

Этот алгоритм генерации двоичной псевдослучайной последовательности основывается на проблеме факторизации больших чисел. Он используется в криптосистеме Блюма-Голдвассера с открытым ключом и состоит из шести шагов.

Шаг 1. Генерируются два достаточно больших секретных случайных (и различных) простых числа 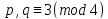и вычисляется

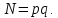
Шаг 2. Выбрать случайное стартовое целое число 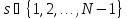так, что НОД Вычислить .

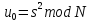Шаг 3. Для 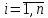выполнить шаги 4, 5.

Шаг 4. Вычислить

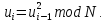
Шаг 5. Вычислить как самый младший бит двоичного представления числа .

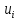Шаг 6. Сформировать выходную последовательность

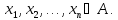
Пример кода реализации BBS на С++:

#include "stdafx.h"

#include <iostream>

#include <cmath>

using namespace std;

typedef long double ll;

class bbs{

ll p, q, N, seed, actual;

ll gcd(ll a, ll b){

if(b == 0) return a;

return gcd(b, fmod(a,b));

}

public:

bbs(ll p, ll q, ll s){

this->p = p;

this->q = q;

this->seed = s;

N = p*q;

actual = s;

}

ll getrandom(){

ll r = fmod(actual*actual,N);

actual = r;

return r;

}

ll getirandom(int i){

ll g = gcd(p, q);

ll lcm = p*q/g;

ll exp = 1;

for(int j = 1; j <= i; ++j) exp = fmod((exp+exp),lcm);

ll x0 = seed*seed;

ll r = x0;

for(int j = 2; j <= exp; ++j) r = fmod((r*x0),N);

return r;

}

};

int main(){

ll p = 7;

ll q = 11;

ll s = 3;

ll N = p*q;

bbs b(p, q, s);

int n = 1000;

cout << n << endl;

for(int i = 0; i < n; ++i) {

cout << b.getrandom()/N << endl;

}

}

На сегодняшний день этот алгоритм является, пожалуй, наиболее надежным ГПСЧ. Для вскрытия начального состояния или угадывания следующего элемента псевдослучайной последовательности атакующий должен знать числа p и q.

У генератора BBS есть только один недостаток — это крайне низкая скорость. Для увеличения производительности на каждом шаге генерации можно возвращать вместо одного, log(log N) бит. Это позволит увеличить скорость не снижая криптостойкости.

СПЕЦИАЛЬНЫЕ РЕАЛИЗАЦИИ

Существует целый ряд практически используемых ГПСЧ которые разрабатывались с учетом криптографической стойкости, например

1) Алгоритм Ярроу (англ. Yarrow algorithm) который пытается определить энтропию входных данных. Он используется в FreeBSD, OpenBSD и Mac OS X.

2) Алгоритм Fortuna (англ. Fortuna algorithm), наследник алгоритма Ярроу.

3) Специальный файл ОС UNIX /dev/random, в частности, /dev/urandom, реализованный в Linux.

4) Функция CryptGenRandom предоставленная в CryptoAPI компании Microsoft.

Алгоритм Yarrow

Алгоритм разработан Брюсом Шнайером, Джоном Келси и Нилсом Фергусом из компании Counterpane Internet Security. Алгоритм не запатентован и свободен от лицензионных отчислений, для его использования не требуется получение лицензии. Ярроу включен в поставку Mac OS X, OpenBSD, и FreeBSD в качестве /dev/random устройства. Для генерации требуется два алгоритма:

1) Односторонняя хеш-функция 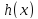, с отпечатком размером –бит.

2) Блочный шифр 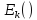с ключом длиной –бит и –битным блоком.

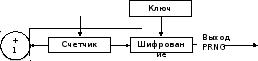
Рис.3. механизм генерации Yarrow

Для генерации следующих –бит псевдослучайной последовательности счётчик увеличивается на 1 и зашифровывается блочным шифром, используя ключ :

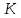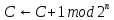
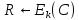
где - выход псевдослучайной последовательности, а 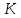- текущий ключ.

Если в какой-то момент ключ оказался скомпрометирован, нужно предотвратить утечку предыдущих выходных значений, которые атакующий может получить. Описанный механизм не имеет такой защиты от утечки, поэтому дополнительно ведётся подсчёт количества блоков псевдослучайных последовательностей, выданных на выход. Как только будет достигнут некий лимит 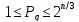, генерируется –битовый выход и устанавливается как ключ.

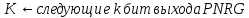
Следует выбирать весьма консервативное значение , в Yarrow оно задано как 10.

Заключение

Таким образом безопасность криптографических систем часто зависит от некоторых данных, которые должны быть известны лишь авторизованным пользователям и которые должно быть трудно угадать злоумышленнику. Примерами таких данных могут быть сессионные ключи, инициализирующие вектора, соль, уникальные параметры в функциях ЭЦП и многие другие объекты. Чтобы достичь требуемого уровня непредсказуемости при условии частой генерации случайных чисел, требуется надёжный источник случайных чисел.

К сожалению, многие криптографические приложения не обладают надежным источником случайных последовательностей значений, таких как, например, тепловой шум в электрических цепях или точное время между парой срабатываний счётчика Гейгера. Вместо этого приходится использовать генераторы псевдослучайных чисел. Успешная атака на ГПСЧ может вскрыть многие криптографические системы независимо от того, насколько тщательно они были спроектированы. Более того, требуется лишь одно успешное проникновение, чтобы скомпрометировать всю систему. Именно поэтому ГПСЧ изначально должны проектироваться с достаточной криптографической стойкостью, чтобы исключить уязвимость криптосистемы с данной стороны.

Список использованной литературы:

1. Шнайер.Б. Прикладная криптография: Протоколы, алгоритмы, исходные тексты на языке Си: Пер. с англ./ Шнайер.Б. – М.: ТРИУМФ, 2003. – 816 с.

2. Математические и компьютерные основы криптологии: Учеб. пособие для студ. метматич. и инженерно- технических спец. вузов. – Минск: ООО «Новое знание», 2003. – 382 с.

3. Дональд Э. Кнут. Искусство программирования: Пер. с англ./ Дональд Э. Кнут. – М.: Вильямс, 2000. — Т. 2. Получисленные алгоритмы. — 832 с.

4. Белова.И.М. Компьютерное моделирование./ Белова.И.М. — М.: МГИУ, 2007. — 81 c.

5. Ситкарев Г.А. Алгоритм Yarrow — краткий обзор./Ситкарев Г.А. – Сыктывкарский Государственный Университет. Лаборатория Программирования и Прикладной Математики. – Режим доступа: http://amplab.syktsu.ru