4. Билинейные функции, квадратичные формы.

   1. Билинейные формы. Квадратичные формы.

Пусть V – линейное пространство над полем P. Функция, ставящая в соответствие паре векторов вещественное число, и обладающая свойствами линейности называется билинейной формой. Другими словами, функция называется билинейной, если

1. ,

2. ,

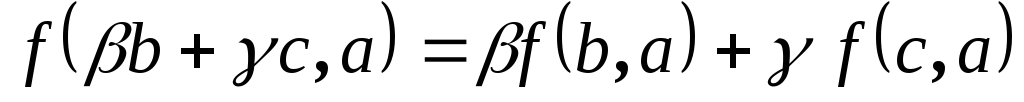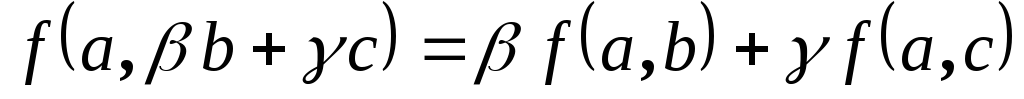где ,.

Примером билинейной функции является скалярное произведение.

Теорема 4.6 Билинейная форма полностью определяется своими значениями на базисных векторах.

Доказательство. Пусть - базисV. Разложим векторы b и c по базису ,. Тогда из линейности выводим. Теорема доказана.

Обозначим через столбец, составленный из координат вектораb, а через – матрицу, на пересеченииi-ой строки и j-го столбца которой расположено значение билинейной формы от базисных векторов . Легко убедиться в равенстве. Матрицаназывается матрицей билинейной формыf в базисе .

Следствие 4.7 Билинейная форма полностью определяется своей матрицей.

Билинейная форма называется симметричной, если ее значение не меняется от перестановки аргументов, то есть .

Следствие 4.8 Билинейная форма симметрична тогда и только тогда, когда найдется базис, в котором ее матрица симметрична.

Доказательство. Если билинейная форма симметричная, то в любом базисе ее матрица симметрична. Обратно, пусть в некотором базисе матрица билинейной формы симметричная. Тогда .

Квадратичной формой называется значение билинейной формы от одного аргумента, то есть f(x,x).

Одну и ту же квадратичную форму можно получить из разных билинейных форм. Например, квадратичную форму можно получить из следующих билинейных форм, где.

Между квадратичными формами и симметричными билинейными формами существует взаимно однозначное соответствие, определяемое формулой 0,25(f(x+y,x+y)-f(x-y,x-y)). Матрица симметричной билинейной формы, соответствующей квадратичной форме, называется матрицей квадратичной формы.

2. Полуторалинейные формы. Эрмитовы формы.

Пусть V – линейное пространство над полем комплексных чисел C. Функция, ставящая в соответствие паре векторов комплексное число, и обладающая свойствами линейности по первому аргументами и «почти линейностью» по второму, называется полуторалинейной формой. Точнее, функция называется полуторалинейной, если

1. ,

2. ,

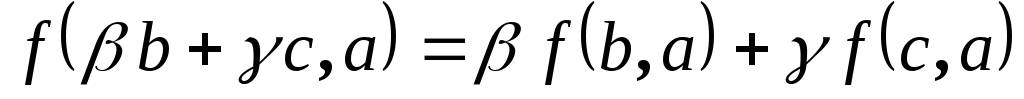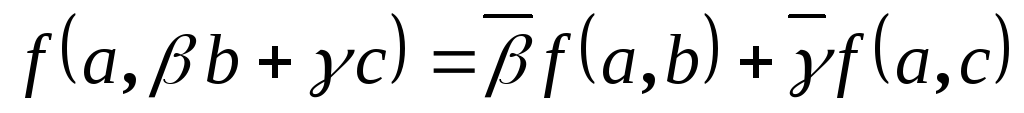где ,.

Примером полуторалинейной функции является скалярное произведение в унитарном пространстве.

Теорема 4.7. Полуторалинейная форма полностью определяется своими значениями на базисных векторах.

Доказательство. Пусть - базисV. Разложим векторы b и c по базису ,. Тогда. Теорема доказана.

Обозначим через столбец, составленный из координат вектораb, а через – матрицу, на пересеченииi-ой строки и j-го столбца которой расположено значение полуторалинейной формы от базисных векторов . Легко убедиться в равенстве, где черта обозначает знак комплексного сопряжения. Матрицаназывается матрицей полуторалинейной формыf в базисе .

Следствие 4.9 Полуторалинейная форма полностью определяется своей матрицей.

Полуторалинейная форма называется эрмитовой, если ее значение меняется от перестановки аргументов на комплексно сопряженное, то есть .

Следствие 4.10 Полуторалинейная форма является эрмитовой тогда и только тогда, когда найдется базисe, в котором ее матрица удовлетворяет равенству .

Для эрмитовых форм определен аналог квадратичной формы .

Значение квадратичной эрмитовой формы – всегда вещественное число, так как .