
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
- •Процесс ортогонализации.
- •Ортогональное дополнение. Ортогональная проекция и составляющая.
- •Геометрический смысл определителя матрицы Грама. Неравенство Адамара.
- •. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.
- •Псевдорешения. Метод наименьших квадратов.
- •Нормальное решение
- •Нормальное псевдорешение.
- •Унитарное пространство.
- •Билинейные функции, квадратичные формы.
- •Билинейные формы. Квадратичные формы.
- •Полуторалинейные формы. Эрмитовы формы.
- •Изменение матрицы билинейной (полуторалинейной) формы при изменении базиса.
- •Приведение квадратичных форм (симметричных билинейных форм, эрмитовых форм) к простейшему виду.
- •Метод выделения квадратов (Лагранжа).
- •Приведение квадратичных форм к нормальному виду элементарными преобразованиями
- •Закон инерции квадратичных форм.
- •Теорема Якоби
- •Критерий Сильвестра.
- •Квадрики.
- •Алгебраическая поверхность
- •Уравнение квадрики.
- •Изменение квадрики при аффинном преобразовании
- •Приведение уравнения квадрики к простейшему виду
- •Аффинная классификация кривых второго порядка.
- •Аффинная классификация поверхностей второго порядка
- •Линейный оператор
- •Линейный оператор. Матрица линейного оператора.
- •Примеры линейных операторов.
- •Матрица линейного оператора.
- •Изменение матрицы линейного оператора при изменении базиса.
- •Алгебра линейных операторов.
- •Простейший вид матрицы линейного оператора.
- •Эквивалентность матриц
- •Ранг, дефект линейного оператора.
- •Линейное преобразование
- •Линейное преобразование. Его матрица
- •Изменение матрицы линейного преобразования при изменении базиса.
- •Алгебра линейных преобразований.
- •Инвариантные пространства
- •Собственные векторы и собственные числа. Характеристическое уравнение.
- •Коэффициенты характеристического уравнения. След матрицы.
- •Диагонализируемые преобразования
- •Теорема Шура
- •Сопряженные преобразования.
- •Линейное преобразование и билинейные функции
- •Сопряженное преобразование. Свойства.
- •Нормальное преобразование и его свойства.
- •Ортогональные преобразования
- •Самосопряженное преобразование.
- •Полярное разложение
- •Приведение квадратичных форм
- •Приведение квадратичных форм к главным осям.
- •Приведение пары квадратичных форм
- •Первый способ
- •Пучок матриц
- •Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.
- •Ортогональная классификация кривых второго порядка
- •Ортогональная классификация поверхностей второго порядка.
- •Аннулирующий многочлен
- •Аннулирующий многочлен вектора.
- •Аннулирующий многочлен подпространства
- •Функции от матриц
- •Вычисление линейных рекуррентных последовательностей
Вычисление линейных рекуррентных последовательностей
Последовательность
![]() называется линейной рекуррентной, если
существуют такие коэффициенты
называется линейной рекуррентной, если
существуют такие коэффициенты![]() ,
что для любогоn
справедливо равенство
,
что для любогоn
справедливо равенство
![]() .
Для задания линейной рекуррентной
последовательности, кроме ее коэффициентов,
необходимо знать первые k членов
.
Для задания линейной рекуррентной
последовательности, кроме ее коэффициентов,
необходимо знать первые k членов![]() ,
которые называются начальными условиями.
Рассмотрим задачу выражения n-го члена
последовательности через его номер и
начальные условия.
,
которые называются начальными условиями.
Рассмотрим задачу выражения n-го члена
последовательности через его номер и
начальные условия.
Обозначим
через
![]() вектор
столбец, состоящий изk
компонент
вектор
столбец, состоящий изk
компонент
![]() ,
через
,
через![]() — матрицу размерами
— матрицу размерами![]() вида
вида .
По правилу перемножения матриц имеем:
.
По правилу перемножения матриц имеем:![]() .
Многократным применением полученной
формулы выводим
.
Многократным применением полученной
формулы выводим![]() .
Задача вычисленияn-го
члена последовательности свелась, тем
самым, к вычислению матрицы
.
Задача вычисленияn-го
члена последовательности свелась, тем
самым, к вычислению матрицы
![]() .
.
Характеристический
многочлен
![]() матрицыА
равен
матрицыА
равен
![]() .
Разделим многочлен
.
Разделим многочлен![]() на
на![]() с остатком. Пусть
с остатком. Пусть![]() ,
где
,
где![]() - остаток от деления. Подставив вместоλ
матрицу А,
получим
- остаток от деления. Подставив вместоλ
матрицу А,
получим
![]() .
По теореме Гамильтона-Кэли каждая
матрица является корнем своего
характеристического уравнения, то есть
.
По теореме Гамильтона-Кэли каждая
матрица является корнем своего
характеристического уравнения, то есть![]() ,
где 0 - нулевая матрица. Таким образом,
,
где 0 - нулевая матрица. Таким образом,![]() ,
и задача вычисления
,
и задача вычисления![]() свелась к вычислению многочленаr(λ).
свелась к вычислению многочленаr(λ).
Разложим
многочлен
![]() на линейные множители
на линейные множители![]() ,
где
,
где![]() .
Для каждого неотрицательногоj
строго меньшего
.
Для каждого неотрицательногоj
строго меньшего
![]() справедливо равенство
справедливо равенство![]() ,
где
,
где![]() -j-ая
производная характеристического
многочлена. Продифференцировав j
раз равенство
-j-ая
производная характеристического
многочлена. Продифференцировав j
раз равенство
![]() и, подставив в него
и, подставив в него![]() , получим
, получим![]() .
Этими условиями многочленr(λ)
степени k-1
определяется однозначно. В литературе
задача вычисления многочлена по таким
условиям носит название «интерполяционный
многочлен Лагранжа-Сильвестра».
.
Этими условиями многочленr(λ)
степени k-1
определяется однозначно. В литературе
задача вычисления многочлена по таким
условиям носит название «интерполяционный
многочлен Лагранжа-Сильвестра».
В
качестве примера вычислим n-ый
член линейной рекуррентной последовательности
![]() ,
где
,
где
![]() .
Положим
.
Положим
![]() .
Характеристический многочлен равен
.
Характеристический многочлен равен![]() .
Остаток от деления
.
Остаток от деления![]() на
на![]() удовлетворяет соотношениям
удовлетворяет соотношениям![]() и
и![]() .
Единственный многочлен первой степени,
удовлетворяющий этим условиям, равен
.
Единственный многочлен первой степени,
удовлетворяющий этим условиям, равен![]() .
Таким образом,
.
Таким образом,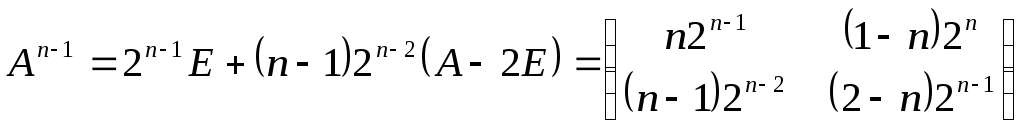 и
и![]() .
.
