
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
- •Процесс ортогонализации.
- •Ортогональное дополнение. Ортогональная проекция и составляющая.
- •Геометрический смысл определителя матрицы Грама. Неравенство Адамара.
- •. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.
- •Псевдорешения. Метод наименьших квадратов.
- •Нормальное решение
- •Нормальное псевдорешение.
- •Унитарное пространство.
- •Билинейные функции, квадратичные формы.
- •Билинейные формы. Квадратичные формы.
- •Полуторалинейные формы. Эрмитовы формы.
- •Изменение матрицы билинейной (полуторалинейной) формы при изменении базиса.
- •Приведение квадратичных форм (симметричных билинейных форм, эрмитовых форм) к простейшему виду.
- •Метод выделения квадратов (Лагранжа).
- •Приведение квадратичных форм к нормальному виду элементарными преобразованиями
- •Закон инерции квадратичных форм.
- •Теорема Якоби
- •Критерий Сильвестра.
- •Квадрики.
- •Алгебраическая поверхность
- •Уравнение квадрики.
- •Изменение квадрики при аффинном преобразовании
- •Приведение уравнения квадрики к простейшему виду
- •Аффинная классификация кривых второго порядка.
- •Аффинная классификация поверхностей второго порядка
- •Линейный оператор
- •Линейный оператор. Матрица линейного оператора.
- •Примеры линейных операторов.
- •Матрица линейного оператора.
- •Изменение матрицы линейного оператора при изменении базиса.
- •Алгебра линейных операторов.
- •Простейший вид матрицы линейного оператора.
- •Эквивалентность матриц
- •Ранг, дефект линейного оператора.
- •Линейное преобразование
- •Линейное преобразование. Его матрица
- •Изменение матрицы линейного преобразования при изменении базиса.
- •Алгебра линейных преобразований.
- •Инвариантные пространства
- •Собственные векторы и собственные числа. Характеристическое уравнение.
- •Коэффициенты характеристического уравнения. След матрицы.
- •Диагонализируемые преобразования
- •Теорема Шура
- •Сопряженные преобразования.
- •Линейное преобразование и билинейные функции
- •Сопряженное преобразование. Свойства.
- •Нормальное преобразование и его свойства.
- •Ортогональные преобразования
- •Самосопряженное преобразование.
- •Полярное разложение
- •Приведение квадратичных форм
- •Приведение квадратичных форм к главным осям.
- •Приведение пары квадратичных форм
- •Первый способ
- •Пучок матриц
- •Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.
- •Ортогональная классификация кривых второго порядка
- •Ортогональная классификация поверхностей второго порядка.
- •Аннулирующий многочлен
- •Аннулирующий многочлен вектора.
- •Аннулирующий многочлен подпространства
- •Функции от матриц
- •Вычисление линейных рекуррентных последовательностей
Приведение квадратичных форм
Приведение квадратичных форм к главным осям.
Рассмотрим
квадратичную форму
![]() .
МатрицаA
является
симметричной. Линейное преобразование,
заданное матрицей A,
является самосопряженным и для этого
преобразования существует ортонормированный
базис из собственных векторов. Другими
словами, найдется ортогональная матрица
T
(
.
МатрицаA
является
симметричной. Линейное преобразование,
заданное матрицей A,
является самосопряженным и для этого
преобразования существует ортонормированный
базис из собственных векторов. Другими
словами, найдется ортогональная матрица
T
(![]() ),
что
),
что![]() ,
где
,
где![]() - собственные числаA.
Поскольку
- собственные числаA.
Поскольку
![]() ,
то квадратичная форма
,
то квадратичная форма![]() ортогональной заменой
ортогональной заменой![]() переходит в форму
переходит в форму![]() .
Приведение квадратичной формы к
каноническому виду ортогональным
преобразованием называется приведением
к главным осям. Полученный факт оформим
в виде теоремы.
.
Приведение квадратичной формы к
каноническому виду ортогональным
преобразованием называется приведением
к главным осям. Полученный факт оформим
в виде теоремы.
Теорема 9.35.
Квадратичная форма![]() при помощи ортогонального преобразования
всегда может быть приведена к канонической
форме
при помощи ортогонального преобразования
всегда может быть приведена к канонической
форме![]() ,
де
,
де![]() - собственные числаA.
- собственные числаA.
Отметим, что для квадратичной формы выполняется закон инерции. Следовательно, используя теорему Якоби, можно определить число положительных и число отрицательных собственных значений. Собственные значения матриц A и A-tE отличаются на t, поэтому, определяя число положительных и отрицательных собственных значений матрицы A-tE, мы, тем самым, определим количество собственных значений матрицы A меньших t. Выбирая различные t можно найти собственные числа с любой точностью.
Приведение пары квадратичных форм
Рассмотрим
задачу выбора базиса в котором пара
квадратичных форм имеют диагональный
вид. Не все пары квадратичных форм можно
одновременно привести к диагональному
виду, например, формы
![]() иxy
привести
нельзя.
иxy
привести
нельзя.
Первый способ
Пусть
даны квадратичные формы
![]() и
и![]() ,
причем квадратичная форма
,
причем квадратичная форма![]() - положительно определена. Тогда введем
скалярное произведение
- положительно определена. Тогда введем
скалярное произведение![]() и найдем ортонормированный базис, а
затем приведем первую квадратичную
форму к главным осям. Поскольку
ортогональное преобразование не меняет
скалярное произведение, то обе квадратичные
формы будут приведены к каноническому
виду.
и найдем ортонормированный базис, а
затем приведем первую квадратичную
форму к главным осям. Поскольку
ортогональное преобразование не меняет
скалярное произведение, то обе квадратичные
формы будут приведены к каноническому
виду.
Пучок матриц
Пусть
даны квадратичные формы
![]() и
и![]() .
Рассмотрим пучок квадратичных форм
.
Рассмотрим пучок квадратичных форм![]() .
Если квадратичные формы
.
Если квадратичные формы![]() и
и![]() заменой координатx=Py
приводятся
к каноническому виду, то все формы из
пучка
заменой координатx=Py
приводятся
к каноническому виду, то все формы из
пучка
![]() приводятся к каноническому виду этой
же заменой координат. Пусть
приводятся к каноническому виду этой
же заменой координат. Пусть![]() и
и![]() ,
тогда
,
тогда![]() .
Из последнего равенства выводим
.
Из последнего равенства выводим![]() ,
то есть многочлен
,
то есть многочлен![]() раскладывается на линейные множители
над полем вещественных чисел. Из равенства
раскладывается на линейные множители
над полем вещественных чисел. Из равенства![]() выводим, чтоi-ый
столбец матрицы P
удовлетворяет
однородной системе уравнений
выводим, чтоi-ый
столбец матрицы P
удовлетворяет
однородной системе уравнений
![]() .
Таким образом, получается следующий
алгоритм приведения пары квадратичных
форм к нормальному виду.
.
Таким образом, получается следующий
алгоритм приведения пары квадратичных
форм к нормальному виду.
Раскладываем многочлен
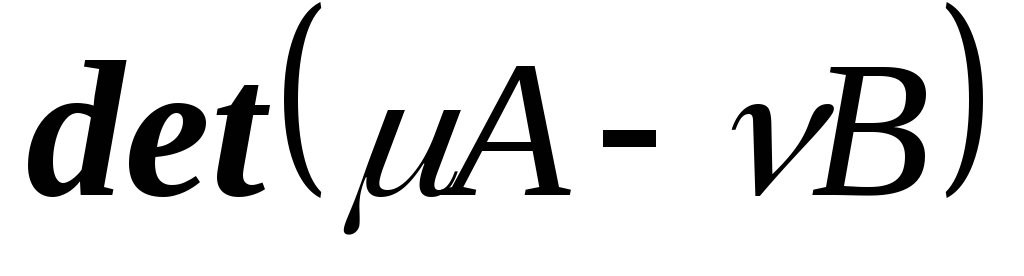 на линейные множители. Если разложения
не существует, то искомой замены
координат не существует.
на линейные множители. Если разложения
не существует, то искомой замены
координат не существует.Для каждого линейного множителя
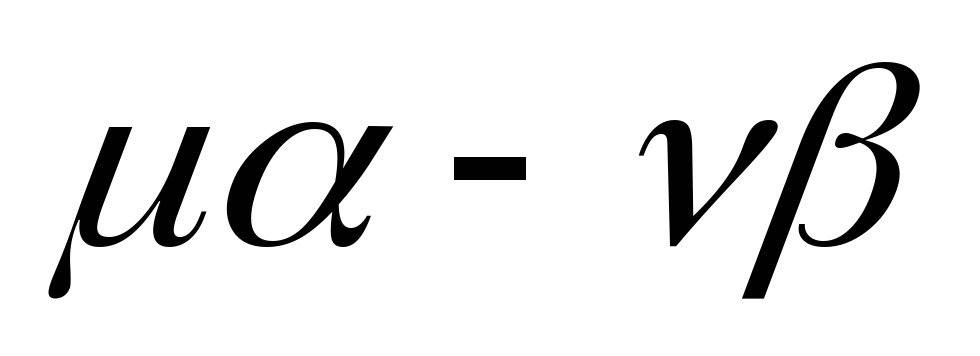 многочлена
многочлена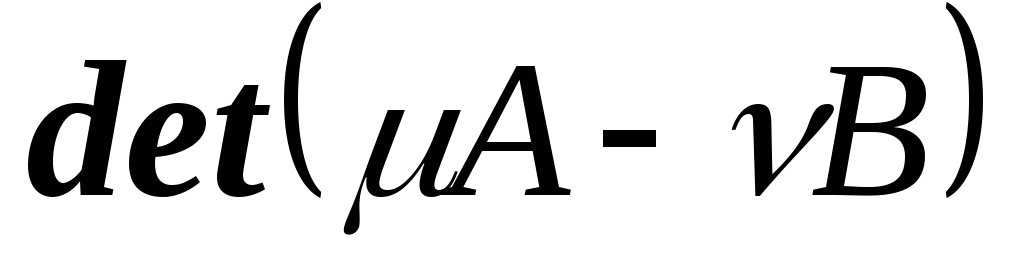 находим базис подпространства
находим базис подпространства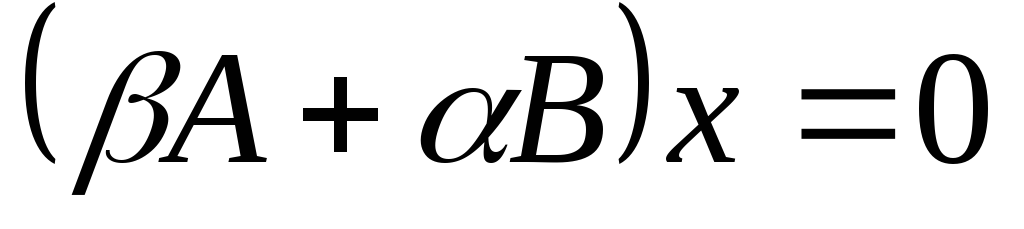 .
Если размерность подпространства
меньше кратности множителя, то искомой
замены координат не существует. В
противном случае, будет построен базис,
в котором квадратичные формы имеют
нормальный вид.
.
Если размерность подпространства
меньше кратности множителя, то искомой
замены координат не существует. В
противном случае, будет построен базис,
в котором квадратичные формы имеют
нормальный вид.
Для обоснования этого подхода требуется показать, что объединение линейно независимых систем векторов, соответствующих разным линейным множителям, образует линейно независимую систему. Доказательство проводится также как и для собственных векторов.
Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.
Рассмотрим задачу упрощения уравнения квадрики с использованием ортогональным преобразованием системы координат. Отметим, что при ортогональной замене координат сохраняются метрические характеристики.
Опишем
алгоритм приведения квадрики
![]() к простейшему виду ортогональным
преобразованием.
к простейшему виду ортогональным
преобразованием.
Приводим квадратичную форму
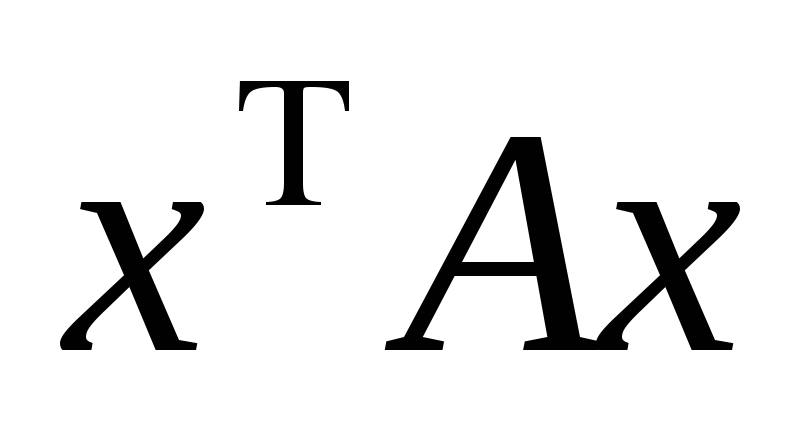 к главным осям ортогональным
преобразованием
к главным осям ортогональным
преобразованием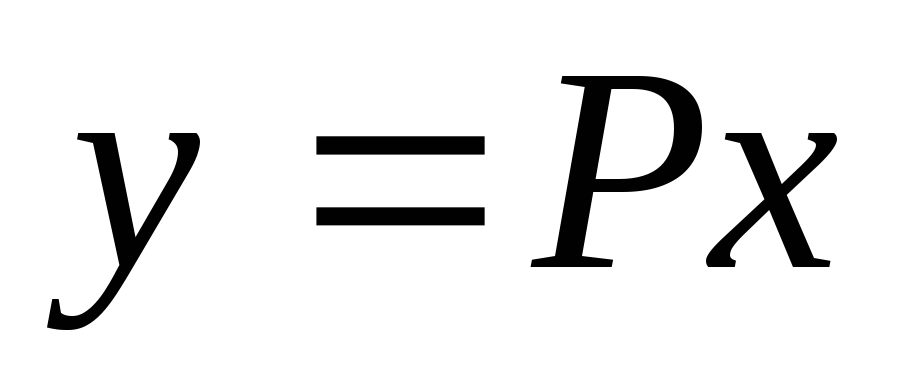 .
В результате получим уравнение квадрики
.
В результате получим уравнение квадрики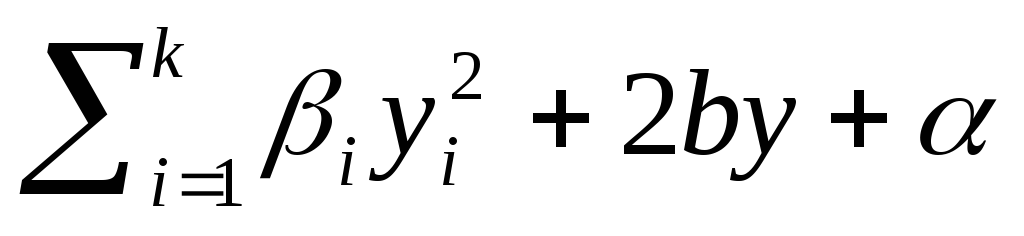 ,
где
,
где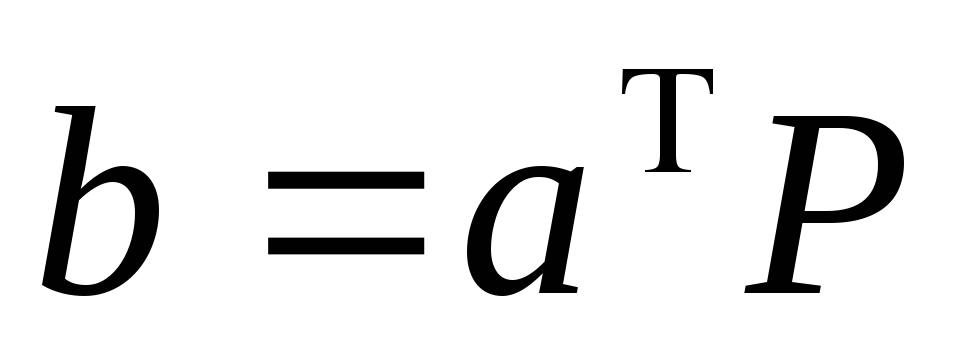 ,k
– ранг матрицы A,
а
,k
– ранг матрицы A,
а
 - ее ненулевые собственные числа.
- ее ненулевые собственные числа.Сдвигом начала координат
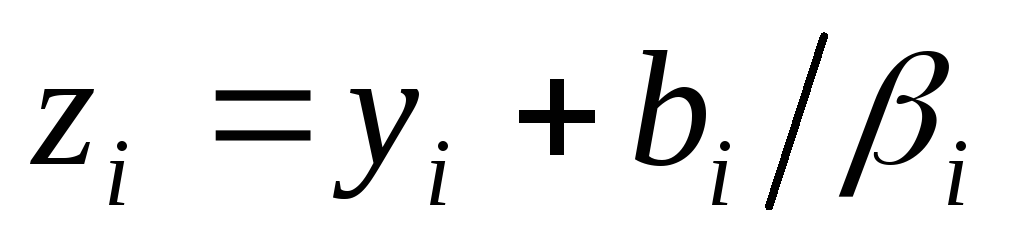 при
при и
и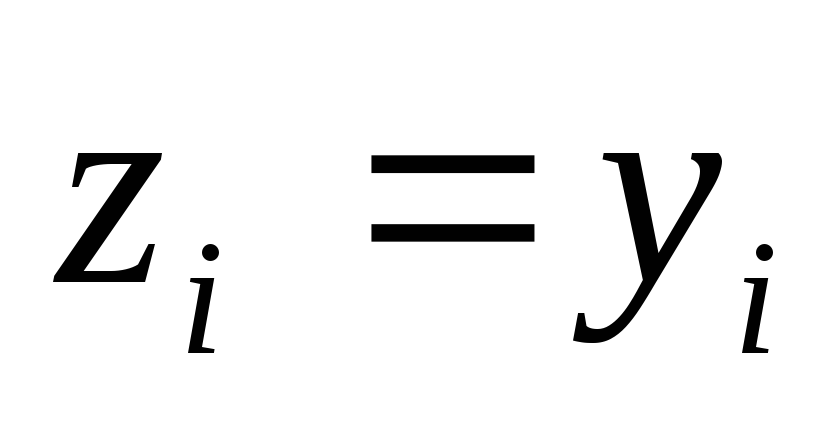 приi>k
приведем квадрику к виду
приi>k
приведем квадрику к виду
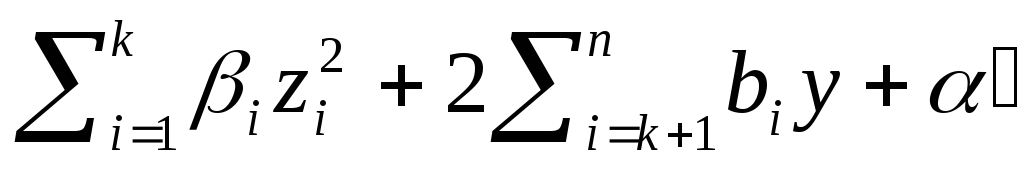 ,
где
,
где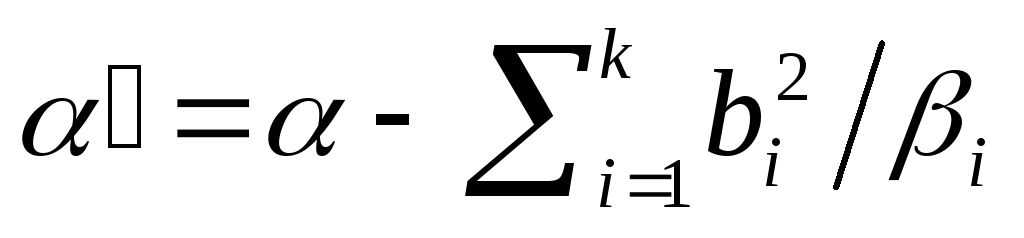 .
Если
.
Если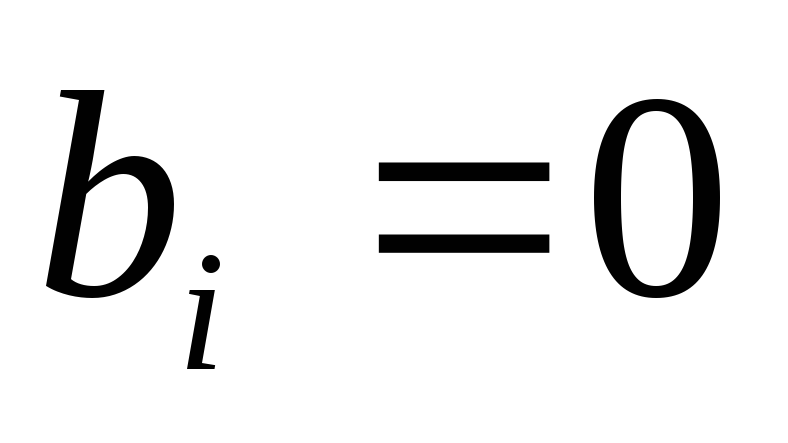 приi>k,
то конец, а иначе перейдем на следующий
шаг.
приi>k,
то конец, а иначе перейдем на следующий
шаг.Положим
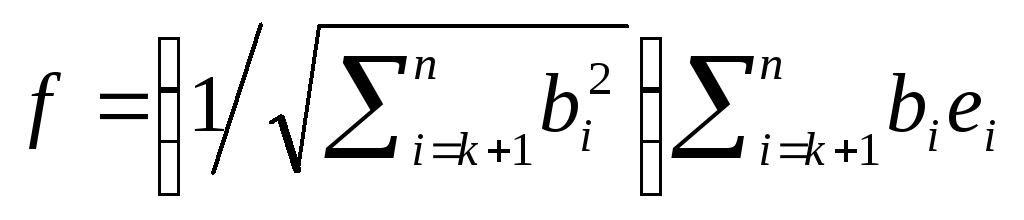 .
Система векторов
.
Система векторов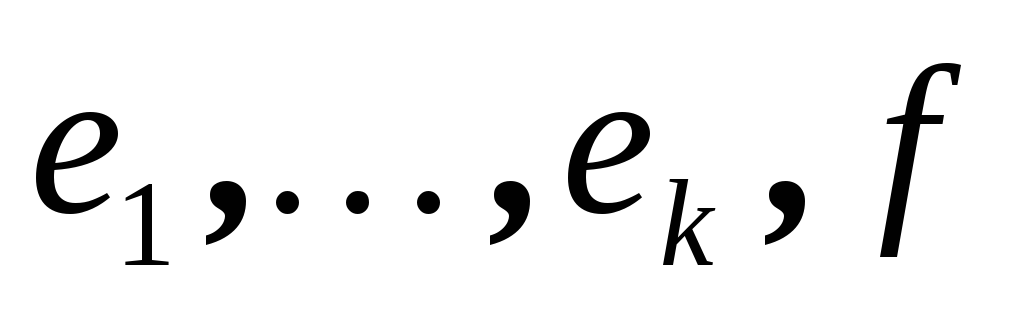 - ортонормированная. Дополним ее до
ортонормированного базиса всего
пространства. ПустьT
– матрица перехода к новому базису.
Сделаем замену переменных
- ортонормированная. Дополним ее до
ортонормированного базиса всего
пространства. ПустьT
– матрица перехода к новому базису.
Сделаем замену переменных
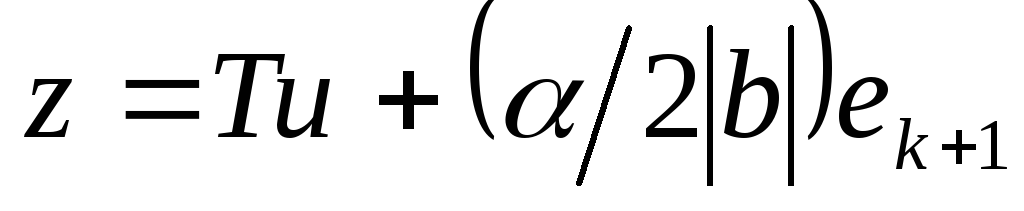 .
Очевидно, сделанная замена является
ортогональной. В новой системе координат
уравнение квадрики
.
Очевидно, сделанная замена является
ортогональной. В новой системе координат
уравнение квадрики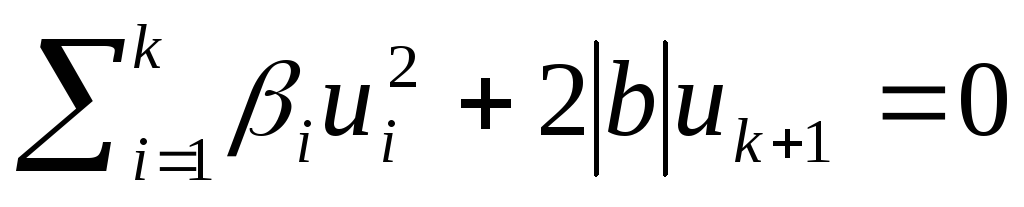 .
.
Оформим доказанное выше в виде теоремы.
Теорема 9.36.
Ортогональным преобразованием, сдвигом
начала координат и умножением на
ненулевое число уравнение квадрики
приводится к одному из следующих четырех
видов![]() ,
,![]() ,
,![]() ,
,![]() .
.
Обозначим
через
![]() сумму всех главных миноровk-го
порядка матрицы A.
Величина
сумму всех главных миноровk-го
порядка матрицы A.
Величина
![]() является коэффициентом характеристического
многочлена
является коэффициентом характеристического
многочлена![]() при
при![]() .
.
Пусть
квадрика
![]() ортогональным
преобразованием x=h+Ty
приводится к виду
ортогональным
преобразованием x=h+Ty
приводится к виду
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
Поскольку T
ортогональная матрица, то
.
Поскольку T
ортогональная матрица, то
![]() ,
и, значит,
,
и, значит,
![]() ,
гдеk=1,…,n.
Кроме того,
,
гдеk=1,…,n.
Кроме того,
![]() ,
и, следовательно,
,
и, следовательно,![]() .
Тем самым установлен следующий факт.
.
Тем самым установлен следующий факт.
Свойство 9.26
При ортогональном преобразовании не
меняются следующие величины
![]() ,
где k=1,…,n,
и
,
где k=1,…,n,
и
![]() ,
которые называются ортогональными
инвариантами квадрики.
,
которые называются ортогональными
инвариантами квадрики.
К сожалению, ортогональные инварианты не всегда позволяют установить простейший тип квадрики.
Свойство 9.27.
Пусть![]() и
и![]() ,
тогда
,
тогда![]() не меняется при ортогональном
преобразовании.
не меняется при ортогональном
преобразовании.
Доказательство.
При ортогональном преобразовании (без
сдвига) величины
![]() не меняются. Пусть квадратичная форма
не меняются. Пусть квадратичная форма![]() приводится к главным осям ортогональной
заменой координат
приводится к главным осям ортогональной
заменой координат![]() .
Пусть
.
Пусть![]() - ортогональное преобразование квадрики.
Поскольку
- ортогональное преобразование квадрики.
Поскольку
![]() ,
то для доказательства утверждения
достаточно рассмотреть случай, когда
,
то для доказательства утверждения
достаточно рассмотреть случай, когда
![]() - диагональная матрица и преобразование
заключается в сдвиге на векторh
начала координат. Если
- диагональная матрица и преобразование
заключается в сдвиге на векторh
начала координат. Если
![]() ,
то
,
то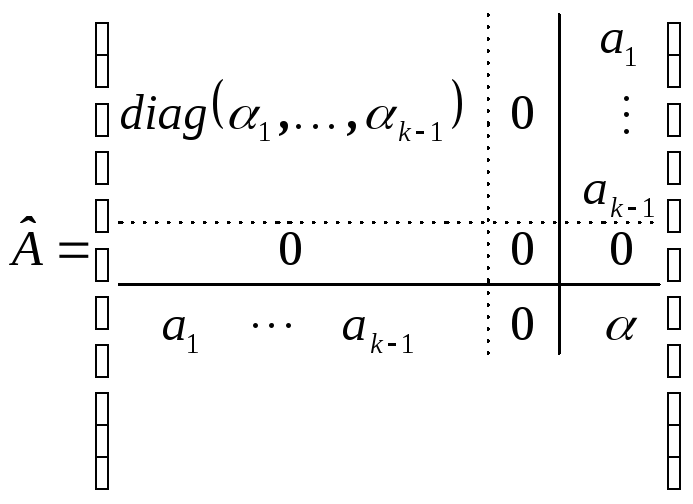 .
В этой матрице единственный минорk
порядка, не содержащий нулевых строк,
определитель которого не зависит от
сдвига. Следовательно, утверждение в
данном случае доказано. Пусть
.
В этой матрице единственный минорk
порядка, не содержащий нулевых строк,
определитель которого не зависит от
сдвига. Следовательно, утверждение в
данном случае доказано. Пусть
![]() ,
тогда
,
тогда .
В этой матрице единственный минорk
порядка, не содержащий нулевых строк,
определитель которого не зависит от
сдвига. Следовательно, утверждение и в
данном случае доказано.
.
В этой матрице единственный минорk
порядка, не содержащий нулевых строк,
определитель которого не зависит от
сдвига. Следовательно, утверждение и в
данном случае доказано.
Величины
![]() называются полуинвариантами ортогонального
преобразования.
называются полуинвариантами ортогонального
преобразования.
Набор инвариантов и полуинвариантов квадрики позволяет однозначно установить простейшее уравнение квадрики.
