2. Ранг, дефект линейного оператора.

Образ нуля равен нулю. Действительно, , отсюда.

Множество векторов из W, образ которых равен 0, называется ядром линейного оператора. Ядро линейного преобразования обозначим (). Ядро является подпространствомW (докажите) и его размерность называют дефектом и обозначают .

Множество всех образов векторов из W обозначают (). Множество образов является подпространствомV (докажите), его размерность называют рангом линейного оператора и обозначают .

Теорема 6.21..

Доказательство. Пусть – базис . По определению для каждого вектора существует прообразизW. Система векторов является линейно независимой. Действительно, из равенства, выводим, или

. В силу линейной независимости, все коэффициенты равны 0, и система является линейно независимой. Аналогично показывается, что пересечение линейной оболочки векторови состоит только из нулевого вектора. Действительно, из включения , выводим, и далее,. Для любого вектораx из W найдутся коэффициенты, что , и. Таким образомW представляется в виде прямой суммы линейной оболочки векторов и . Теорема вытекает из свойства прямой суммы.

Следствие 6.15. Можно выбрать базисы в пространствахW и V так, чтобы матрица линейного оператора имела диагональный вид, причем по диагонали расположены 1 и 0. Количество ненулевых элементов на диагонали равно рангу оператора.

Доказательство. Пусть иимеют тот же смысл, что и в доказательстве предыдущей теоремы. Дополним векторыдо базисаV, а векторы до базисаW векторами из . Полученные базисы обозначим через и, соответственно. Построим матрицу линейного оператора в этих базисах. Заметим,, а координаты векторав базисеравны (0,…,0,1,0,…,0), где 1 стоит наi-ом месте. Таким образом, матрица линейного оператора в этих базисах имеет диагональный вид, причем по диагонали расположены 1 и 0. Количество 1 равно рангу оператора.

7. Линейное преобразование

   1. Линейное преобразование. Его матрица

Однозначное отображение линейного пространстваV над числовым полем P в себя называется линейным преобразованием, если оно сохраняет линейность, то есть для любыхи.

Линейное преобразование полностью определяется своими значениями на базисных векторах. Действительно, пусть базисV. Вектор x разложим по базису , где- координаты вектораx. По свойству линейного преобразования имеем . Перейдем в последнем равенстве от равенства векторов к равенству их координат, которое можно записать используя матричное умножение следующим образом. Матрицаназываетсяматрицей линейного преобразования и обозначается . Матрица линейного преобразования связывает координаты образа с координатами исходного вектора.

2. Изменение матрицы линейного преобразования при изменении базиса.

Поскольку линейное преобразование частный случай линейного оператора, то можно воспользоваться полученной ранее формулой , гдеP – матрица перехода. Матрицы A и B называются подобными, если существует невырожденная матрица P, что . Вопрос о подобии матриц сводится к решению системы линейных уравнений, где в роли неизвестных выступают элементы матрицыP, с дополнительным нелинейным условием .

3. Алгебра линейных преобразований.

На множестве всех линейных преобразований пространства V расмотрим операции:

1. Умножение на число: .

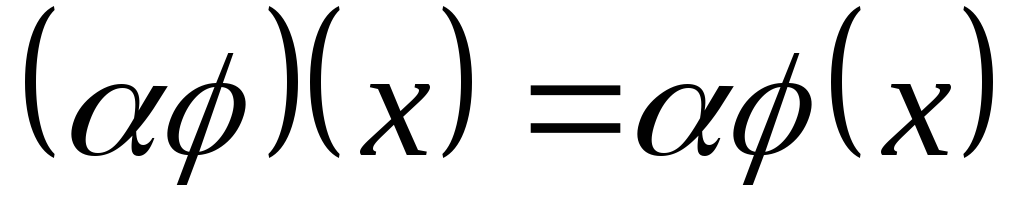2. Сложение (вычитание)

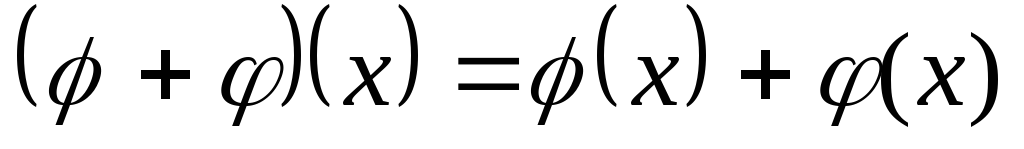
3. Умножение .

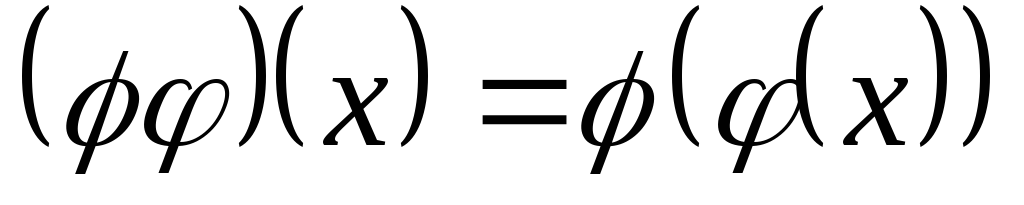Легко проверить линейность всех этих преобразований и вывести следующие формулы, связывающие их матрицы

1. 

2. 

3. 

Линейное преобразование, переводящее каждый вектор в себя, называется тождественным преобразованием и обозначается . В любом базисе матрица тождественного преобразования равна единичной.

Пусть - некоторый многочлен,- линейное преобразование пространстваV. Сопоставим многочлену линейное преобразование. Будем говорить, что преобразованиеполучено подстановкойв многочлен. Матрицаможет быть вычислена по формуле.

Свойство 7.14. Пусть. Тогда.