
- •Геометрия на плоскости и в пространстве.
- •Скалярное произведение.
- •Векторное и смешанное произведение.
- •Уравнение прямой и плоскости в пространстве
- •Евклидово пространство. Скалярное произведение.
- •Изменение матрицы Грама при изменении базиса.
- •Ортогональность.
- •Процесс ортогонализации.
- •Ортогональное дополнение. Ортогональная проекция и составляющая.
- •Геометрический смысл определителя матрицы Грама. Неравенство Адамара.
- •. Расстояния. Псевдорешения. Нормальные решения. Нормальные псевдорешения.
- •Псевдорешения. Метод наименьших квадратов.
- •Нормальное решение
- •Нормальное псевдорешение.
- •Унитарное пространство.
- •Билинейные функции, квадратичные формы.
- •Билинейные формы. Квадратичные формы.
- •Полуторалинейные формы. Эрмитовы формы.
- •Изменение матрицы билинейной (полуторалинейной) формы при изменении базиса.
- •Приведение квадратичных форм (симметричных билинейных форм, эрмитовых форм) к простейшему виду.
- •Метод выделения квадратов (Лагранжа).
- •Приведение квадратичных форм к нормальному виду элементарными преобразованиями
- •Закон инерции квадратичных форм.
- •Теорема Якоби
- •Критерий Сильвестра.
- •Квадрики.
- •Алгебраическая поверхность
- •Уравнение квадрики.
- •Изменение квадрики при аффинном преобразовании
- •Приведение уравнения квадрики к простейшему виду
- •Аффинная классификация кривых второго порядка.
- •Аффинная классификация поверхностей второго порядка
- •Линейный оператор
- •Линейный оператор. Матрица линейного оператора.
- •Примеры линейных операторов.
- •Матрица линейного оператора.
- •Изменение матрицы линейного оператора при изменении базиса.
- •Алгебра линейных операторов.
- •Простейший вид матрицы линейного оператора.
- •Эквивалентность матриц
- •Ранг, дефект линейного оператора.
- •Линейное преобразование
- •Линейное преобразование. Его матрица
- •Изменение матрицы линейного преобразования при изменении базиса.
- •Алгебра линейных преобразований.
- •Инвариантные пространства
- •Собственные векторы и собственные числа. Характеристическое уравнение.
- •Коэффициенты характеристического уравнения. След матрицы.
- •Диагонализируемые преобразования
- •Теорема Шура
- •Сопряженные преобразования.
- •Линейное преобразование и билинейные функции
- •Сопряженное преобразование. Свойства.
- •Нормальное преобразование и его свойства.
- •Ортогональные преобразования
- •Самосопряженное преобразование.
- •Полярное разложение
- •Приведение квадратичных форм
- •Приведение квадратичных форм к главным осям.
- •Приведение пары квадратичных форм
- •Первый способ
- •Пучок матриц
- •Приведение квадрики ортогональным преобразованием. Ортогональные инварианты и полуинварианты.
- •Ортогональная классификация кривых второго порядка
- •Ортогональная классификация поверхностей второго порядка.
- •Аннулирующий многочлен
- •Аннулирующий многочлен вектора.
- •Аннулирующий многочлен подпространства
- •Функции от матриц
- •Вычисление линейных рекуррентных последовательностей
Лекции по аналитической геометрии и высшей алгебре (прикладная информатика) 2 семестр.
Геометрия на плоскости и в пространстве.
Целью данного раздела состоит в рассмотрении таких геометрических понятий как расстояние, площадь, объём с последующим обобщением этих понятий и их переносом на произвольные линейные пространства.
Скалярное произведение.
Определение
1.1. Скалярным произведением
геометрических векторовaиbназывается число,
равное произведению длин этих векторов
на косинус угла между ними. Скалярное
произведение векторов обозначают![]() .
.
Из
определения следует, что длина вектора
равна
![]() .
.
Приведём свойства скалярного произведения.
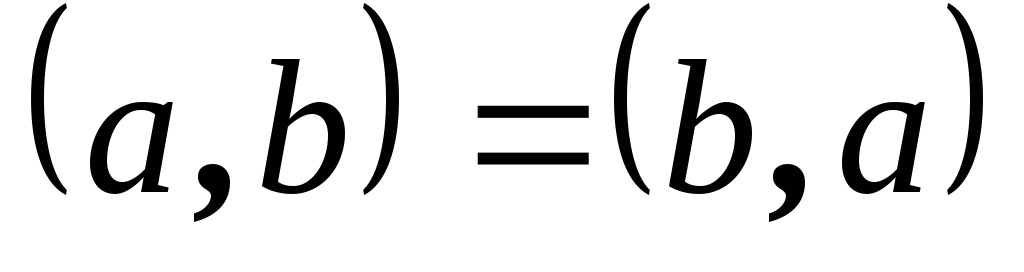 .
Симметричность
.
Симметричность Линейность
Линейность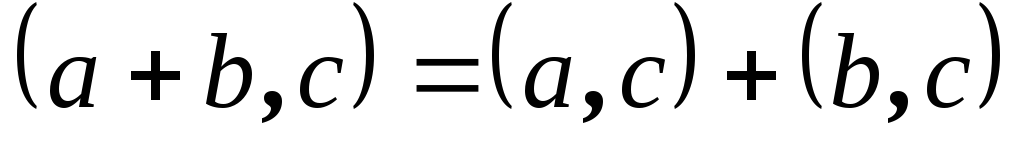
В
доказательстве нуждается только третье
равенство. Если c=0,
то равенство очевидно. Пусть
![]() .
Проекция вектораb
на c
равна
.
Проекция вектораb
на c
равна
![]() .
.
И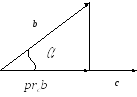 з
равенства
з
равенства![]() и приведённой выше формулы выводим
и приведённой выше формулы выводим![]() .
Приравняем коэффициенты при векторе c
в левой и правой частях равенства
.
Приравняем коэффициенты при векторе c
в левой и правой частях равенства![]() и умножим на квадрат длины вектора c,
получим свойство 3.
и умножим на квадрат длины вектора c,
получим свойство 3.
Задание
длин векторов определяет скалярное
произведение. Действительно, из свойств
скалярного произведения выводим
равенство
![]() ,
которое перепишем в виде
,
которое перепишем в виде
![]() .
Таким образом, задание длин векторов
равносильно заданию скалярного
произведения и наоборот.
.
Таким образом, задание длин векторов
равносильно заданию скалярного
произведения и наоборот.
Выразим
скалярное произведение через координаты
перемножаемых векторов. Пусть
![]() - базис пространства векторов, и
- базис пространства векторов, и![]() ,
,![]() - разложения векторов a,b по этому базису.
Тогда по свойствам скалярного произведения
выводим
- разложения векторов a,b по этому базису.
Тогда по свойствам скалярного произведения
выводим![]()
![]()
![]() .
Обозначим через
.
Обозначим через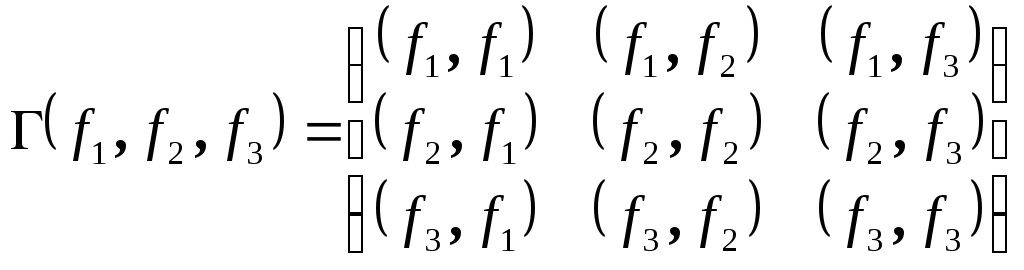 матрицу Грамма от векторов
матрицу Грамма от векторов![]() ,
составленную из скалярных произведений
этих векторов, через
,
составленную из скалярных произведений
этих векторов, через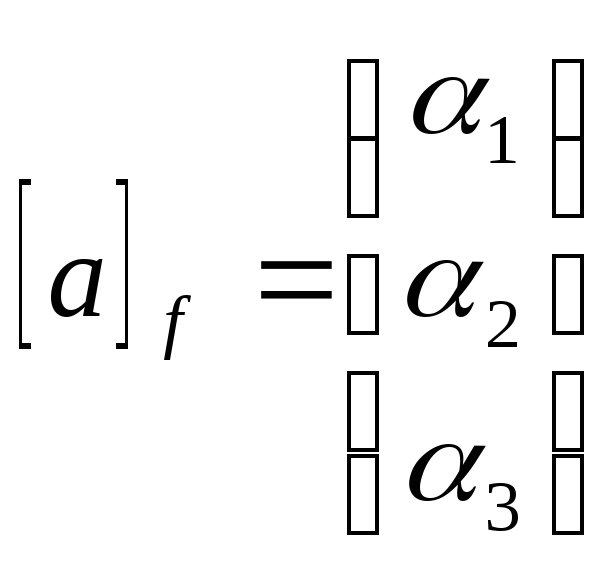 - координаты вектора a в базисе f. В этих
обозначениях скалярное произведение
можно записать с помощью матричных
операций следующим образом
- координаты вектора a в базисе f. В этих
обозначениях скалярное произведение
можно записать с помощью матричных
операций следующим образом![]() .
.
Векторы
называются ортогональными (перпендикулярными)
если угол между ними равен
![]() .
Условие ортогональности векторов
равносильно равенству нулю их скалярного
произведения.
.
Условие ортогональности векторов
равносильно равенству нулю их скалярного
произведения.
Базис
![]() называется ортогональным, если базисные
векторы попарно ортогональны. Матрица
Грамма ортогональной системы векторов
– диагональная. Выражение скалярного
произведения через координаты векторов
в ортогональном базисе принимает более
простой вид, а именно,
называется ортогональным, если базисные
векторы попарно ортогональны. Матрица
Грамма ортогональной системы векторов
– диагональная. Выражение скалярного
произведения через координаты векторов
в ортогональном базисе принимает более
простой вид, а именно,![]() .
.
В
ортогональном базисе скалярное
произведение вектора a на базисный
вектор равно
![]() ,
то есть, координаты вектора a находятся
по формулам
,
то есть, координаты вектора a находятся
по формулам![]() .
.
Ортогональный
базис
![]() ,
в котором длина каждого базисного
вектора равна 1, называется ортонормированным.
В ортонормированном базисе координаты
вектора x определяются по формулам
,
в котором длина каждого базисного
вектора равна 1, называется ортонормированным.
В ортонормированном базисе координаты
вектора x определяются по формулам![]() ,
а скалярное произведение векторов равно
,
а скалярное произведение векторов равно![]() .
.
Векторное и смешанное произведение.
М ножество
всех ортонормированных троек векторов
можно разбить на два класса. Будем
говорить, что тройка имеет левую
ориентацию, если со стороны первого
вектора тройки движение (по кратчайшему
пути) от второго к третьему по часовой
стрелке, в противном случае тройка имеет
правую ориентацию.
ножество
всех ортонормированных троек векторов
можно разбить на два класса. Будем
говорить, что тройка имеет левую
ориентацию, если со стороны первого
вектора тройки движение (по кратчайшему
пути) от второго к третьему по часовой
стрелке, в противном случае тройка имеет
правую ориентацию.
Векторным
произведением
![]() векторов a и b называется вектор,
удовлетворяющий следующим трём условиям:
векторов a и b называется вектор,
удовлетворяющий следующим трём условиям:
Длина вектора
 равна площади параллелограмма натянутого
на векторыa,b.
равна площади параллелограмма натянутого
на векторыa,b.Вектор
 ортогонален векторамa
и b.
ортогонален векторамa
и b.Т
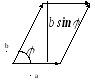 ройка
векторовa,b,
ройка
векторовa,b,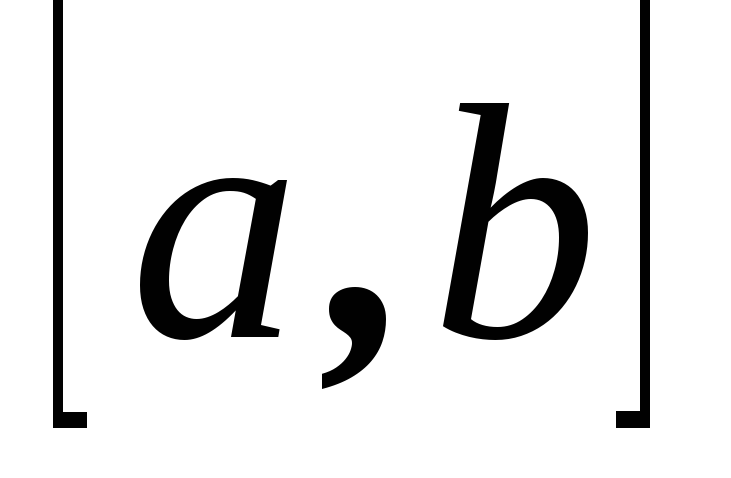 – имеет правую ориентацию.
– имеет правую ориентацию.
Из
определения вытекает, что
![]() .
Если векторыa,b
коллинеарные, то векторное произведение
равно 0. Приведём свойства векторного
произведения.
.
Если векторыa,b
коллинеарные, то векторное произведение
равно 0. Приведём свойства векторного
произведения.
Свойство 1.1
Векторное произведение антикоммутативно,
то есть![]() .
.
Действительно,
модуль векторного произведения не
зависит от порядка сомножителей. Далее,
вектор
![]() коллинеарен вектору
коллинеарен вектору![]() .
Однако, переставляя множителей, мы
должны изменить направление произведения,
чтобы было выполнено условие 3.
.
Однако, переставляя множителей, мы
должны изменить направление произведения,
чтобы было выполнено условие 3.
Смешанным
произведением векторов a,b,c
называется число
![]() и обозначается
и обозначается![]() .
.
Свойство 1.2
Смешанное произведение векторов![]() по модулю равно объёму параллелепипеда
натянутого на тройку векторовa,b,c.
Знак смешанного произведения определяется
ориентацией тройки векторов
a,b,c,
плюс – если тройка правая и минус –
если левая.
по модулю равно объёму параллелепипеда
натянутого на тройку векторовa,b,c.
Знак смешанного произведения определяется
ориентацией тройки векторов
a,b,c,
плюс – если тройка правая и минус –
если левая.
Д оказательство.
По определению смешанного произведения
оказательство.
По определению смешанного произведения
![]() ,
где
,
где![]() - угол между вектором
- угол между вектором![]() и векторным произведением
и векторным произведением![]() ,
а
,
а![]() - угол между векторами
- угол между векторами![]() и
и![]() .
Произведение
.
Произведение![]() равно высоте параллелепипеда, а
равно высоте параллелепипеда, а![]() - площади основания параллелепипеда.
Произведение этих величин равно объёму
параллелепипеда. Знак произведения
определяется знаком
- площади основания параллелепипеда.
Произведение этих величин равно объёму
параллелепипеда. Знак произведения
определяется знаком![]() .
Если угол острый, то тройка векторов
правая и смешанное произведение
положительно. Если угол тупой, то тройка
левая и знак смешанного произведения
отрицательный.
.
Если угол острый, то тройка векторов
правая и смешанное произведение
положительно. Если угол тупой, то тройка
левая и знак смешанного произведения
отрицательный.
Свойство 1.3![]() .
.
Для
доказательства
достаточно заметить, что по модулю все
приведённые величины равны и совпадают
с объёмом параллелепипеда, натянутого
на векторы
![]() ,
а знак определяется в зависимости от
ориентации тройки векторов.
,
а знак определяется в зависимости от
ориентации тройки векторов.
Свойство 1.4.![]()
Доказательство.
Рассмотрим смешанное произведение
![]() .
Выпишем цепочку равенств, используя
свойства смешанного и скалярного
произведения:
.
Выпишем цепочку равенств, используя
свойства смешанного и скалярного
произведения:![]()
![]() .
Вычтем из левой части равенства правую
.
Вычтем из левой части равенства правую![]() и получим равенство
и получим равенство![]() справедливое при любом выбореx.
Положим
справедливое при любом выбореx.
Положим
![]() ,
тогда
,
тогда![]() и, значит,
и, значит,![]() .
.
Свойство 1.5![]()
Доказательство.
![]() .
.
Выразим
координаты векторного произведения
через координаты исходных векторов в
правом ортонормированном базисе. Пусть
![]() и
и![]() .
Используя свойства векторного
произведения, найдём
.
Используя свойства векторного
произведения, найдём![]() ,
,![]() и
и![]() .
Поскольку базис ортонормированный, то
.
Поскольку базис ортонормированный, то
первая
координата
![]() равна
равна![]() ,
вторая координата
,
вторая координата![]() и третья координата
и третья координата![]() .
Таким образом, векторное произведение
может быть получено в результате
раскрытия по третьему столбцу
символического определителя
.
Таким образом, векторное произведение
может быть получено в результате
раскрытия по третьему столбцу
символического определителя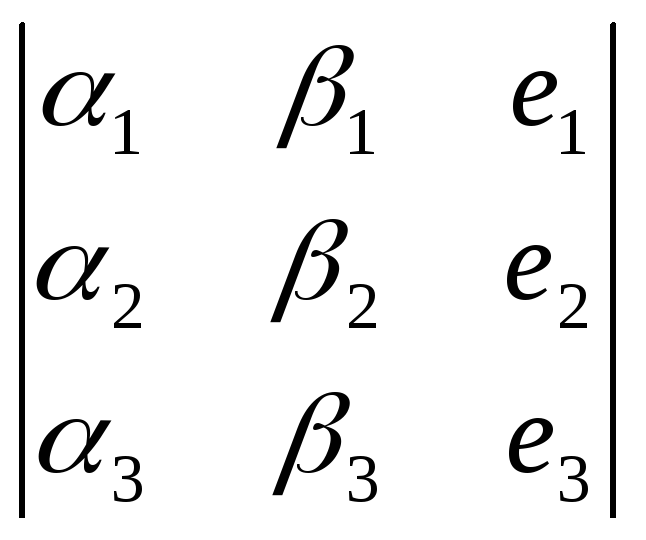 .
.
Выразим
смешанное произведение через координаты
исходных векторов в ортонормированном
базисе. Разложим векторы a,b,c
по базису
![]() ,
,![]() ,
,![]() . Раскроем смешенное произведение
. Раскроем смешенное произведение![]() .
Выражение в правой части есть определитель
матрицы
.
Выражение в правой части есть определитель
матрицы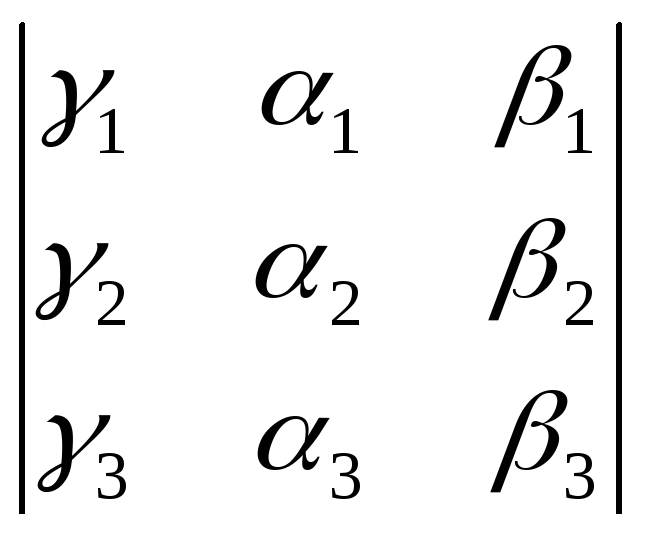 .
.
Таким образом, определитель матрицы, составленной из координат векторов по абсолютной величине равен объёму параллелепипеда натянутого на эти вектора, а его знак показывает ориентацию этой тройки векторов. Знак положителен, если ориентация совпадает с ориентацией базисных векторов и отрицателен, если ориентации не совпадают.
Матрица
Грама от трёх векторов, заданных в
ортонормированном базисе равна
произведению матриц
![]() ,
следовательно, определитель матрицы
Грама равен квадрату объёма параллелепипеда
натянутого на эти векторы.
,
следовательно, определитель матрицы
Грама равен квадрату объёма параллелепипеда
натянутого на эти векторы.
