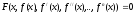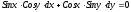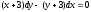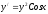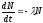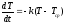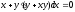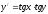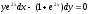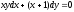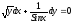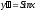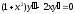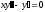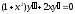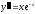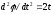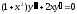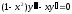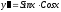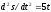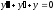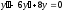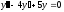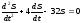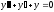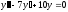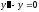- •Государственное бюджетное образовательное учреждение высшего
- •Содержание дисциплинарного модуля «физика и математика»
- •1. Производная функции первого порядка
- •3. Производная второго и высших порядков
- •4. Производная функции нескольких аргументов.
- •5. Дифференциал функции.
- •Неопределённый интеграл
- •2. Определённый интеграл
- •3. Основные свойства определённого интеграла:
- •1. Основные понятия теории обыкновенных дифференциальных уравнений.
- •2. Дифференциальные уравнения первого порядка с разделяющимися переменными:
- •3. Дифференциальные уравнения второго порядка
- •Лабораторная работа
- •Краткая теория
- •I. Проведение статистической обработки результатов исследования
- •II. Нормальный закон распределения
- •Основные свойства кривой Гаусса.
- •2. Правила обработки результатов измерений.
- •III. Проверка распределения эмпирических данных на нормальный закон распределения.
- •1.Построение "Гистограммы".
- •2. Проверка закона распределения случайных величин на нормальность с помощью показателей асимметрии и эксцесса.
- •3. Исследование степени соответствия эмпирических и теоретических данных на нормальный закон распределения (по критерию Колмогорова).
- •IV. Получение статистического материала.
- •Ход работы
- •«Гидродинамика. Гемодинамика»
- •Модуль 2. Магнитные свойства тканей и окружающей среды
- •Ход работы.
- •Внимание!
- •Модульная единица 3 Оптика, квантовая физика, ионизирующие излучения.
- •Занятие 3.2
- •Лабораторная работа
- •Явление преломления света. Закон Снелля
- •Ход работы
- •Занятие 3.3
- •Лабораторная работа
- •Коэффициент пропускания, оптическая плотность.
- •Метод концентрационной колориметрии.
- •Устройство и принцип работы фотоэлектроколориметра.
- •Использование концентрационной колориметрии в медицине.
- •Ход работы:
- •Занятие 3.4
- •Лабораторная работа
- •Естественный и поляризованный свет
- •Поляризатор и анализатор
- •Закон Малюса
- •Вращение плоскости поляризации
- •Поляриметрия
- •Устройство и принцип работы поляриметра
- •Ход работы:
- •Вопросы к зачёту по дисциплинарному модулю «физика и математика»
- •Модуль 2. Процессы переноса в биологических системах, биоэлектрогенез, электрические и магнитные свойства тканей и окружающей среды.
- •Модуль 3. Оптика, квантовая физика, ионизирующие излучения.
- •Механические колебания и волны, акустика. Биофизика слухового анализатора.
- •Гидродинамика. Гемодинамика.
- •Электрическое и магнитное поля.
- •Геометрическая оптика. Преломление, поляризация и поглощение свет.
- •Ионизирующие излучения. Рентгеновская трубка.
- •Дозиметрия
а) не содержащие искомой функции и её производной.
б) не содержащие искомой функции.
в) линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Формулы и закономерности, используемые при решении примеров:
1. Основные понятия теории обыкновенных дифференциальных уравнений.
или
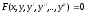 общий вид дифференциального уравнения.
общий вид дифференциального уравнения.
Если
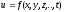 ,
то
,
то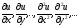 уравнение называетсядифференциальным
уравнением в частных производных.
уравнение называетсядифференциальным
уравнением в частных производных.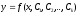 -
общее
решение дифференциального
уравнения порядка k,
где С1,
С2,..,Сk
произвольные постоянные.
-
общее
решение дифференциального
уравнения порядка k,
где С1,
С2,..,Сk
произвольные постоянные.
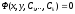 -
общий интеграл
или общее
решение, записанное в неявном виде.
-
общий интеграл
или общее
решение, записанное в неявном виде.
Частные решения, получают из общего решения путём задания определённых численных значений (т.е. задаются начальные условия).
2. Дифференциальные уравнения первого порядка с разделяющимися переменными:
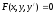 дифференциальное
уравнение первого порядка
дифференциальное
уравнение первого порядка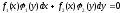 -
дифференциальные уравнения первого
порядка с разделяющимися переменными.
Для того чтобы привести это уравнению
к уравнению с разделёнными переменными
нужно поделить правую и левую части
выражения на
-
дифференциальные уравнения первого
порядка с разделяющимися переменными.
Для того чтобы привести это уравнению
к уравнению с разделёнными переменными
нужно поделить правую и левую части
выражения на
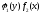 :
: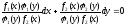
при условии если
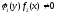 .
.После сокращения получаем:
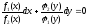
Интегрируем это выражение:
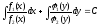 ,
гдеС
– произвольная постоянная. Это выражение
является общим решением уравнения.
,
гдеС
– произвольная постоянная. Это выражение
является общим решением уравнения.Пример: найти общее и частное решения уравнения
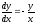 при
при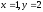 .
.Решение: Разделим переменные. Для этого, умножим обе части уравнения на
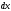 и разделим на
и разделим на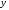 ,и
получим уравнение с разделёнными
переменными:
,и
получим уравнение с разделёнными
переменными: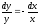 ,
проинтегрируем это уравнение, используя
основные формулы интегрирования:
,
проинтегрируем это уравнение, используя
основные формулы интегрирования:
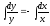 ,
,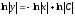 или
или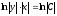 .
Потенцируя последнее равенство, получаем
.
Потенцируя последнее равенство, получаем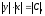
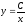 - общее решение.
- общее решение.Из условия, что при
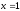 и
и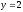 ,
найдём значение С:
,
найдём значение С: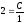 ,
откуда С=2. Частное решение будет иметь
вид
,
откуда С=2. Частное решение будет иметь
вид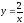 .
.3. Дифференциальные уравнения второго порядка
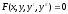 -
общий вид дифференциального уравнения
второго порядка.
-
общий вид дифференциального уравнения
второго порядка.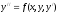 ,
,
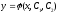 - дифференциальное уравнение второго
порядка, разрешённое относительно
второй производной и его общее решение.
- дифференциальное уравнение второго
порядка, разрешённое относительно
второй производной и его общее решение.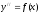 -
дифференциальное
уравнение второго порядка, не содержащее
искомой функции и её первой производной
(решается
двукратным
интегрированием
с введением новой функции, дающей
возможность понизить их
порядок).
-
дифференциальное
уравнение второго порядка, не содержащее
искомой функции и её первой производной
(решается
двукратным
интегрированием
с введением новой функции, дающей
возможность понизить их
порядок).
Пример: найти общее решение уравнения
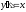 .
.Решение: Пусть
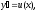 тогда
тогда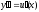 и
и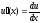 ,
тогда
,
тогда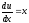 .
.Разделим переменные, проинтегрируем и найдём первую производную:
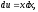
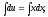
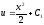 или
или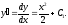
Разделив в последнем уравнении переменные и проинтегрировав его, найдём саму функцию у:
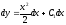 ,
,
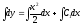 таким образом,
таким образом,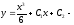 общее решение. С1,
С2
– произвольные постоянные.
общее решение. С1,
С2
– произвольные постоянные.
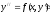 дифференциальное
уравнение второго порядка, не содержащее
искомой функции (решается
двукратным
интегрированием
с введением новой функции, дающей
возможность понизить их
порядок).
дифференциальное
уравнение второго порядка, не содержащее
искомой функции (решается
двукратным
интегрированием
с введением новой функции, дающей
возможность понизить их
порядок).
Пример: найти общее решение уравнения
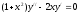 .
.Решение: обозначим
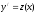 ,
,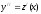 ,
тогда
,
тогда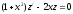 или
или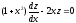 .
Разделим переменные и проинтегрируем:
.
Разделим переменные и проинтегрируем: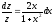 ;
;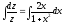 ;
;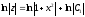 .
Потенцируем последнее выражение:
.
Потенцируем последнее выражение: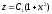 .
Так как
.
Так как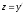 ,
то
,
то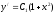 или
или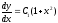 .
Разделив переменные и проинтегрировав,
получим:
.
Разделив переменные и проинтегрировав,
получим: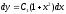 ;
;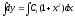 ,
откуда
,
откуда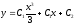 - общее решение исходного уравнения.
- общее решение исходного уравнения.
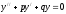 -
линейное
однородное дифференциальное уравнение
второго порядка с постоянными
коэффициентами.
-
линейное
однородное дифференциальное уравнение
второго порядка с постоянными
коэффициентами.
Одним из частных решений этого уравнения является функция
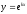 ,
где
,
где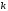 некоторое
число. Тогда:
некоторое
число. Тогда: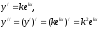
Подставим значения производных и функции в уравнение:
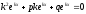 или
или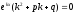 .
Это уравнение называютхарактеристическим
уравнением
данного дифференциального уравнения.
Множитель
.
Это уравнение называютхарактеристическим
уравнением
данного дифференциального уравнения.
Множитель
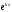 отличен от нуля. Таким образом, чтобы
функция
отличен от нуля. Таким образом, чтобы
функция
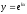 была решением дифференциального
уравнения, необходимо и достаточно,
чтобы
была решением дифференциального
уравнения, необходимо и достаточно,
чтобы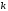 было корнем характеристического
уравнения. Характеристическое уравнение
является алгебраическим уравнением
второй степени, корни которого находят
по формуле:
было корнем характеристического
уравнения. Характеристическое уравнение
является алгебраическим уравнением
второй степени, корни которого находят
по формуле: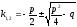
Если корни k1 ≠ k2 - действительные и различные числа, то все решения уравнения даются формулой:
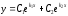 ,
где С1,
С2
– произвольные постоянные.
,
где С1,
С2
– произвольные постоянные.
Если k1=k2=k - действительные и равные числа, то все решения уравнения даются формулой:
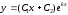 ,
где С1,
С2
– произвольные постоянные.
,
где С1,
С2
– произвольные постоянные.
Если k1,2=
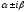
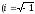 )
- комплексные числа, то все решения
уравнения даются формулой:
)
- комплексные числа, то все решения
уравнения даются формулой:
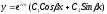 ,
где С1,
С2
– произвольные постоянные.
,
где С1,
С2
– произвольные постоянные.Пример. Найти общее решение дифференциального уравнения:
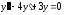
Решение: После ряда преобразований, получаем характеристическое уравнение:
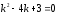 .
Используя формулу
.
Используя формулу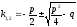 ,
найдём корниk1=1
и k2=3
- действительные и различны, значит
общее решение уравнения:
,
найдём корниk1=1
и k2=3
- действительные и различны, значит
общее решение уравнения:
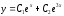 .
.Решить примеры:
а) найти общее и частное решения дифференциального уравнения первого порядка с разделяющимися переменными:
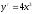 при
при
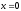 ;
;
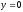
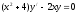 ,
при
,
при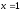 ;
;
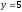
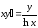 ,
при
,
при
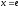 ;
;
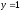
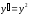 при
при
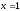 ;
;
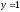
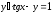 ,
при
,
при
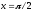 ;
;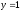
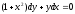 ,
при
,
при
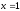 ;
;
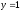
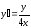 ,
при
,
при
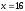 ;
;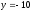

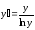 ,
при
,
при
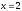 ;
;
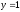
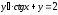 ;
при
;
при
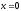 ;
;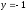
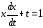 ,
при
,
при
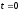 ;
;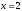
б) найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными:
в) найти общее решение дифференциального уравнения, допускающего понижения порядка:
г) найти общее решение линейного однородного дифференциального уравнения с постоянными коэффициентами:
ЗАНЯТИЕ 1.4
ТЕМА: «ОСНОВЫ ВЫСШЕЙ МАТЕМАТИКИ»
Цель занятия: Контрольная работа.
Студент должен уметь:
Использовать формулы для определения производной сложной функции, использовать правила и методы нахождения первообразной функции, вычислять определённый интеграл, находить общее решение дифференциальных уравнений.
В каждом варианте контрольной работы пять заданий:
Найти производную сложной функции.
Найти первообразную функции.
Вычислять определённый интеграл.
Найти общее решение дифференциального уравнения первого порядка с разделяющимися переменными.
Найти общее решение дифференциального уравнения второго порядка с постоянными коэффициентами.
(при выполнении заданий можно использовать справочную литературу)