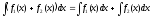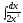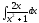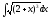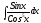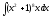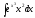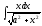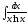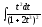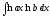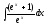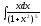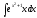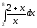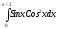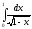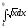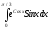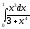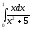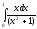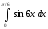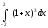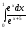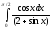- •Государственное бюджетное образовательное учреждение высшего
- •Содержание дисциплинарного модуля «физика и математика»
- •1. Производная функции первого порядка
- •3. Производная второго и высших порядков
- •4. Производная функции нескольких аргументов.
- •5. Дифференциал функции.
- •Неопределённый интеграл
- •2. Определённый интеграл
- •3. Основные свойства определённого интеграла:
- •1. Основные понятия теории обыкновенных дифференциальных уравнений.
- •2. Дифференциальные уравнения первого порядка с разделяющимися переменными:
- •3. Дифференциальные уравнения второго порядка
- •Лабораторная работа
- •Краткая теория
- •I. Проведение статистической обработки результатов исследования
- •II. Нормальный закон распределения
- •Основные свойства кривой Гаусса.
- •2. Правила обработки результатов измерений.
- •III. Проверка распределения эмпирических данных на нормальный закон распределения.
- •1.Построение "Гистограммы".
- •2. Проверка закона распределения случайных величин на нормальность с помощью показателей асимметрии и эксцесса.
- •3. Исследование степени соответствия эмпирических и теоретических данных на нормальный закон распределения (по критерию Колмогорова).
- •IV. Получение статистического материала.
- •Ход работы
- •«Гидродинамика. Гемодинамика»
- •Модуль 2. Магнитные свойства тканей и окружающей среды
- •Ход работы.
- •Внимание!
- •Модульная единица 3 Оптика, квантовая физика, ионизирующие излучения.
- •Занятие 3.2
- •Лабораторная работа
- •Явление преломления света. Закон Снелля
- •Ход работы
- •Занятие 3.3
- •Лабораторная работа
- •Коэффициент пропускания, оптическая плотность.
- •Метод концентрационной колориметрии.
- •Устройство и принцип работы фотоэлектроколориметра.
- •Использование концентрационной колориметрии в медицине.
- •Ход работы:
- •Занятие 3.4
- •Лабораторная работа
- •Естественный и поляризованный свет
- •Поляризатор и анализатор
- •Закон Малюса
- •Вращение плоскости поляризации
- •Поляриметрия
- •Устройство и принцип работы поляриметра
- •Ход работы:
- •Вопросы к зачёту по дисциплинарному модулю «физика и математика»
- •Модуль 2. Процессы переноса в биологических системах, биоэлектрогенез, электрические и магнитные свойства тканей и окружающей среды.
- •Модуль 3. Оптика, квантовая физика, ионизирующие излучения.
- •Механические колебания и волны, акустика. Биофизика слухового анализатора.
- •Гидродинамика. Гемодинамика.
- •Электрическое и магнитное поля.
- •Геометрическая оптика. Преломление, поляризация и поглощение свет.
- •Ионизирующие излучения. Рентгеновская трубка.
- •Дозиметрия
Формулы и закономерности, используемые при решении примеров:
Неопределённый интеграл
 -
неопределённый интеграл, где
-
неопределённый интеграл, где
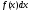 – подынтегральное выражение,
– подынтегральное выражение, – подынтегральная функция,
– подынтегральная функция,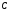 – постоянная интегрирования, а
– постоянная интегрирования, а – переменная интегрирования.
– переменная интегрирования.
1. Основные свойства неопределённого интеграла:
Производная от неопределённого интеграла равна подынтегральной функции:
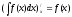
Дифференциал от неопределённого интеграла равен подынтегральному выражению:
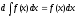
Интеграл от дифференциала первообразной равен самой первообразной и дополнительному слагаемому С:
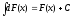
Постоянный множитель k можно выносить за знак неопределённого интеграла:
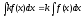
Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от слагаемых:
Основные формулы интегрирования.
1)
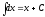 8)
8)
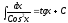
2)
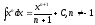 9)
9)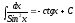
3)
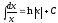 10)
10)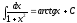
4)
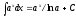 11)
11)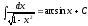
5)
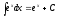 12)
12)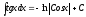
6)
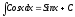
 13)
13)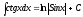
7)
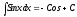
Простейшие способы интегрирования.
Непосредственное интегрирование.
Этот способ основан на прямом использовании свойств неопределённых интегралов и формул интегрирования.
Пример: вычислить интеграл
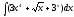 .
.Решение: Используя свойства неопределённого интеграла получаем -
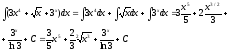
Интегрирование подстановкой (заменой переменных).
Способ заключается в переходе от данной переменной интегрирования к другой переменной для упрощения подынтегрального выражения и приведения его к одному из табличных.
Пример: вычислить а)
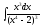 ;
б)
;
б)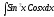 .
.Решение: а) введём подстановку
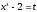 .
.Продифференцируем левую часть подстановки по х, а правую по t:
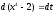 ;
;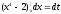 ;
;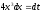 ,откуда
,откуда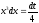 .
Тогда
.
Тогда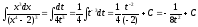 .
.Подставив вместо t его значение
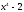 ,
получим
,
получим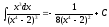 .
.б) вычислим интеграл, используя метод подстановки:
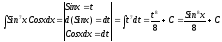
2. Определённый интеграл
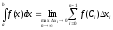 -
определённый интеграл, где а
– нижний предел интегрирования, b
– верхний
предел интегрирования.
-
определённый интеграл, где а
– нижний предел интегрирования, b
– верхний
предел интегрирования.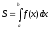 -
площадь криволинейной трапеции
(геометрический смысл определённого
интеграла)
-
площадь криволинейной трапеции
(геометрический смысл определённого
интеграла)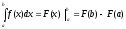 -
формула
Ньютона – Лейбница,
где
-
формула
Ньютона – Лейбница,
где
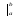 - знак двойной подстановки.
- знак двойной подстановки.
3. Основные свойства определённого интеграла:
Определённый интеграл не зависит от обозначения переменной интегрирования:
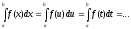
Определённый интеграл от суммы конечного числа непрерывных функций, заданных на отрезке [a,b] равен сумме определённых интегралов от слагаемых функций:
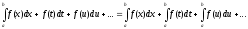
Постоянный множитель k можно вынести за знак определённого интеграла:
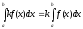
Если верхний и нижний пределы интегрирования поменять местами, то определённый интеграл сохранит абсолютную величину, но изменит свой знак на противоположный, т.е.
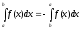
Если пределы интегрирования равны между собой, т.е. a=b, то определённый интеграл равен нулю.
Если существуют интегралы
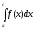 и
и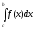 ,
то существует также интеграл
,
то существует также интеграл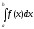 для любого взаимного расположения
точек
для любого взаимного расположения
точек
Если подынтегральная функция на отрезке интегрирования сохраняет постоянный знак, то интеграл представляет собой точек того же знака, что и функция, т.е. если
 то и
то и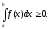
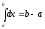 при
a><b
при
a><b
Пример: вычислить интегралы: а)
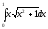 ,
б)
,
б)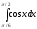
Решение:
а)
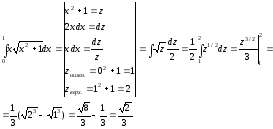
б)
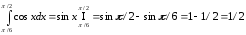
Решить примеры:
а) Вычислить неопределённые интегралы:
б) вычислить определённые интегралы
Вычислить площадь фигуры, заключённой между кривой
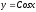 и осью Ох в пределах от 0 до/2.
(использовать формулу для вычисления
площадей плоских фигур
и осью Ох в пределах от 0 до/2.
(использовать формулу для вычисления
площадей плоских фигур
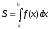 )
)
ЗАНЯТИЕ 1.3
ТЕМА: «ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО И ВТОРОГО ПОРЯДКА»
Цель занятия:Изучить дифференциальные уравнения первого и второго порядка с разделяющимися переменными, линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Дифференциальные уравнения используются при изучении различных явлений и процессов в физике, химии, биологии и медицине. А также в фармации, астрофизике, кибернетике, социологии и других областях науки. Сформулировав задачу на языке дифференциальных уравнений, специалист любой профессии получает в руки готовый аппарат для численного решения задачи изучения качественных особенностей этого решения
Студент должен знать: Основные методы и правила решения дифференциальных уравнений первого и второго порядка с разделяющимися переменными, а так же линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Студент должен уметь: Решать дифференциальные уравнения первого и второго порядка с разделяющимися переменными, линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Вопросы, рассматриваемые на занятии:
Основные понятия теории обыкновенных дифференциальных уравнений.
Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальные уравнения второго порядка с разделяющимися переменными: