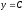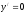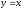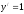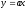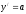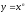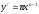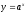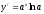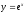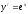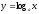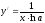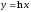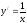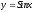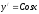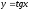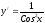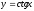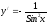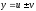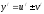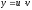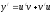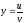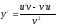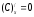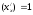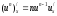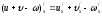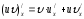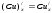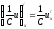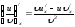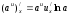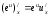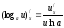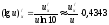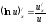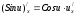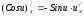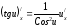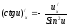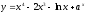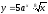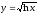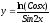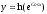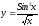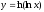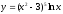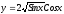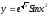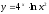- •Государственное бюджетное образовательное учреждение высшего
- •Содержание дисциплинарного модуля «физика и математика»
- •1. Производная функции первого порядка
- •3. Производная второго и высших порядков
- •4. Производная функции нескольких аргументов.
- •5. Дифференциал функции.
- •Неопределённый интеграл
- •2. Определённый интеграл
- •3. Основные свойства определённого интеграла:
- •1. Основные понятия теории обыкновенных дифференциальных уравнений.
- •2. Дифференциальные уравнения первого порядка с разделяющимися переменными:
- •3. Дифференциальные уравнения второго порядка
- •Лабораторная работа
- •Краткая теория
- •I. Проведение статистической обработки результатов исследования
- •II. Нормальный закон распределения
- •Основные свойства кривой Гаусса.
- •2. Правила обработки результатов измерений.
- •III. Проверка распределения эмпирических данных на нормальный закон распределения.
- •1.Построение "Гистограммы".
- •2. Проверка закона распределения случайных величин на нормальность с помощью показателей асимметрии и эксцесса.
- •3. Исследование степени соответствия эмпирических и теоретических данных на нормальный закон распределения (по критерию Колмогорова).
- •IV. Получение статистического материала.
- •Ход работы
- •«Гидродинамика. Гемодинамика»
- •Модуль 2. Магнитные свойства тканей и окружающей среды
- •Ход работы.
- •Внимание!
- •Модульная единица 3 Оптика, квантовая физика, ионизирующие излучения.
- •Занятие 3.2
- •Лабораторная работа
- •Явление преломления света. Закон Снелля
- •Ход работы
- •Занятие 3.3
- •Лабораторная работа
- •Коэффициент пропускания, оптическая плотность.
- •Метод концентрационной колориметрии.
- •Устройство и принцип работы фотоэлектроколориметра.
- •Использование концентрационной колориметрии в медицине.
- •Ход работы:
- •Занятие 3.4
- •Лабораторная работа
- •Естественный и поляризованный свет
- •Поляризатор и анализатор
- •Закон Малюса
- •Вращение плоскости поляризации
- •Поляриметрия
- •Устройство и принцип работы поляриметра
- •Ход работы:
- •Вопросы к зачёту по дисциплинарному модулю «физика и математика»
- •Модуль 2. Процессы переноса в биологических системах, биоэлектрогенез, электрические и магнитные свойства тканей и окружающей среды.
- •Модуль 3. Оптика, квантовая физика, ионизирующие излучения.
- •Механические колебания и волны, акустика. Биофизика слухового анализатора.
- •Гидродинамика. Гемодинамика.
- •Электрическое и магнитное поля.
- •Геометрическая оптика. Преломление, поляризация и поглощение свет.
- •Ионизирующие излучения. Рентгеновская трубка.
- •Дозиметрия
1. Производная функции первого порядка
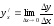 -
производная функции;
-
производная функции;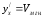 -
мгновенная скорость (физический смысл
производной)
-
мгновенная скорость (физический смысл
производной)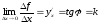 -
угловой коэффициент касательной к
графику функции в некоторой точке
(геометрический смысл производной).
-
угловой коэффициент касательной к
графику функции в некоторой точке
(геометрический смысл производной).
Основные формулы и правила дифференцирования:
Пример: найти производную функций: а)
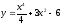 ;
;б)
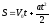 ,
,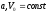 .
.Решение:
а) по формулам дифференцирования 12, 3, 4 и 1 находим
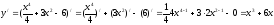 ;
;б) используя формулы 12, 3, 2, 4находим
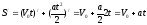 .
.
Сложная функция и её производная:
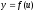 ,
где
,
где
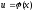 .
.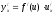
Основные формулы дифференцирования сложных функций:
Пример: найти производную сложной функции
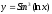 .
.Решение: по формулам дифференцирования 3, 13 находим:
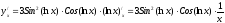
3. Производная второго и высших порядков
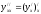 -
производная второго порядка
-
производная второго порядка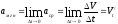 -
мгновенное ускорение (физический смысл
производной второго порядка);
-
мгновенное ускорение (физический смысл
производной второго порядка);
Пример: Найти
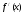 ,
,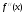 ,
,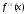 для функции
для функции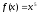
Решение:
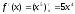 ,
,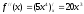 ,
,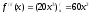 и т.д.
и т.д.4. Производная функции нескольких аргументов.
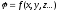 -
функция нескольких аргументов
-
функция нескольких аргументов
()/x, y= const, ; ()/y, z= const, ; ()/z, x= const, - частные производные.
z= const x= const y= const
Пример: найти частные производные функции
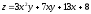 .
.Решение:
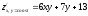
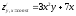 .
.5. Дифференциал функции.
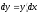 -
дифференциал функции
-
дифференциал функции
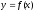 ;
;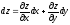 -
полный дифференциал функции, зависящей
от нескольких аргументов
-
полный дифференциал функции, зависящей
от нескольких аргументов
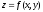
Пример: Электрохимический потенциал вычисляется по формуле:
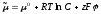 ,
, где
где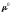 -
постоянная растворителя,R
– универсальная газовая постоянная,
Т – абсолютная температура в Кельвинах,
С – концентрация вещества, z
– заряд атома, F
– число Фарадея,
-
постоянная растворителя,R
– универсальная газовая постоянная,
Т – абсолютная температура в Кельвинах,
С – концентрация вещества, z
– заряд атома, F
– число Фарадея,
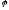 - потенциал
электрического поля.
- потенциал
электрического поля.Найти: а) частные производные
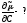 ;
;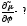 б) полный
дифференциал
б) полный
дифференциал
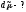
Решение: а)
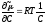 ;
;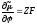 ;
;б)

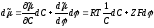
Решить примеры:
а) Найти производные:
Найти производные второго порядка:
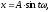 где
где
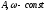
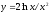
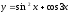
ЗАНЯТИЕ 1.2
ТЕМА: «ПЕРВООБРАЗНАЯ ФУНКЦИИ. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ»
Цель занятия: Изучить свойства первообразной функции, неопределённый и определённый интегралы.
Студент должен знать: Методы вычисления определённых и неопределённых интегралов, их свойства.
Студент должен уметь: Вычислять, используя основные свойства неопределённого и определённого интегралов, применять методы интегрирования.
Вопросы, рассматриваемые на занятии:
Понятие о первообразной функции и неопределённый интеграл.
Основные свойства неопределённых интегралов и способы их интегрирования.
Определённый интеграл и его свойства. Формула Ньютона-Лейбница.
Основные свойства определённых интегралов и способы их интегрирования.