Выборочный метод

Опр.:Статистической совокупностью называют множество однородных предметов или явлений.

Опр.: Числоnэлементов этого множества называетсяобъёмомсовокупности.

Опр.: Наблюдаемые значенияx_i признакаXназывают вариантами. Варианты расположенные в возрастающей последовательности называютсядискретнымвариационным рядом.

Опр.:Под частотой mзначения признака понимают число членов совокупности с данной вариантой.

Опр.: Отношения частоты к объёму статистической совокупности называют

относительной частотойзначения признака.

W=

Опр.: Соответствие между вариантами вариационного ряда и их частотами (или относительными частотами) называют статистическим распределением выборки.

xi	X1	X2	X3		xk
ni	N1	N2	N3		nk

Опр.: Средним выборочным называют величину

_B =(2)

Опр.: ДисперсиейпризнакаXпо отношению к его среднему арифметическому называют величинуD_B(x)=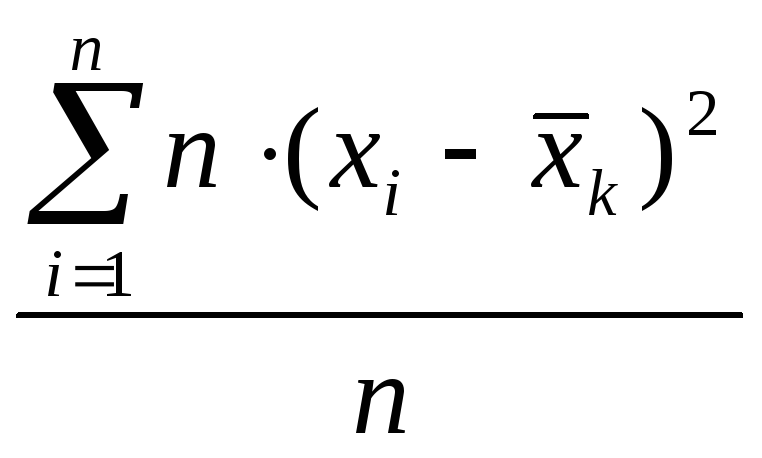(3)

Опр.: Квадратный корень из дисперсии называют среднимквадратичным отклонением G(x)=распределения относительных частот.

Опр.: Эмпирической функцией распределения называют функцию определяющую для каждого значения относительную частоту событий (X<x), т.е.F^*(x)=w(X<x)=, где -число вариант меньшихx, а -объём выборки

Опр.: Полигоном частот называют ломаную, отрезки, которой соединяют точки (x_1,n₁),(x_2,n₂),(x_k,n_k)

Опр.: Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются частичные интервалы длиннойl_i ,а высотой

Пример выполнения лабораторной работы №1“ Первичная обработка данных“

Цель работы: Овладеть методом вычисления ,составление эмпирической функции распределения и гистограммы частот.

Задание: По данной выборке составить статистическое распределение, вычислить, составить эмпирическую функцию

xi	17	18	19	20	21	22	23
ni	7	7	3	1	3	2	2

1. Тогда ряд распределения относительных частот имеет вид

Xi	17	18	19	20	21	22	23
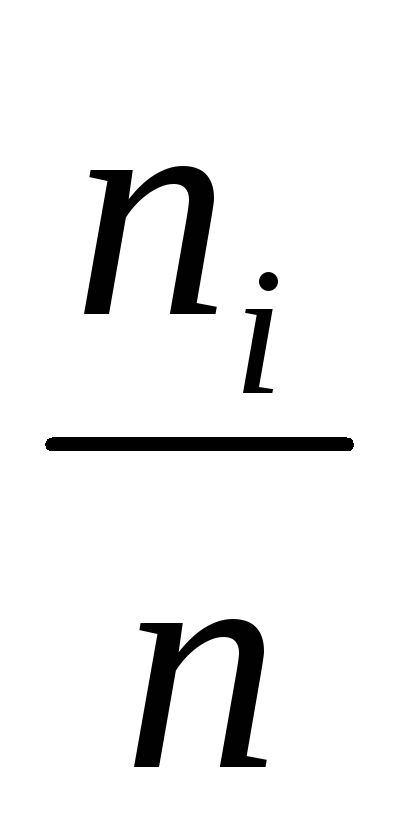
W=	0,28	0,28	0,12	0,04	0,12	0,08	0,08

2. Вычислить среднюю выборочную :

3. Дисперсия признака XравнаD_B(x)=

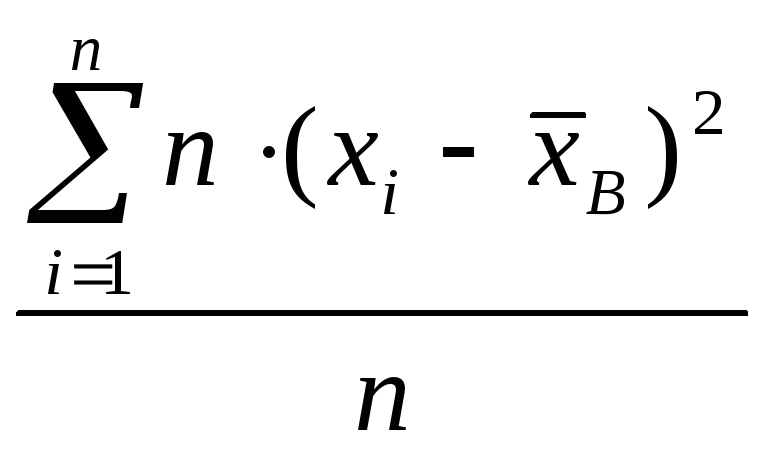
5.Тогда среднее квадратическое отклонение

6.Составим функцию распределения

а)x₁=17-наименьшая варианта значитF^*(x₃)=0 приx

б) x₂=18 , значениеx18, именноx₁=17 наблюдалось 7 раз

F^*(x)=при 17x18

в) x₃=19 значениеx19 ,а именноx₂=18 и x₁=17 встречались 14 раз т.е.

F^*(x)=при 18x19

Аналогично F^*(x)=при 14x20

F^*(x)=при 20x21

F^*(x)=при 21x22

F^*(x)=при 22x23

Так как x=23 –наибольшая варианта, тоF^*(x)=1 приx23

Функция распределения имеет вид

F^*(x)=

График функции распределения F^*(x)

F^*(x)

1

0,96

0,84

0,72

0,68

0,56

0,28

17 18 19 20 21 22 23 X

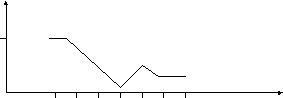
7)Построим полигон частот по точкам (17,7) ; (18;7) ; (19;3) ; (20; 1) ; (21;3); (22;2) ; (23;2)

n_i

7,5

17 18 19 20 21 22 23 x_i

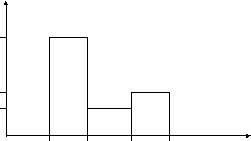
8)Построить гистограмму частот

Для этого разобьем вариантный ряд на интервалы равной длины h, в нашем случаеh=2

Составим таблицу

	17-19	19-21	21-23
ni	15	4	6

7,5

3 3

2

n 17 19 21 23