
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 3
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
- •Контрольная работа № 4
Контрольная работа № 3
Вариант 4.
Задание 1. Найти неопределенные интегралы:
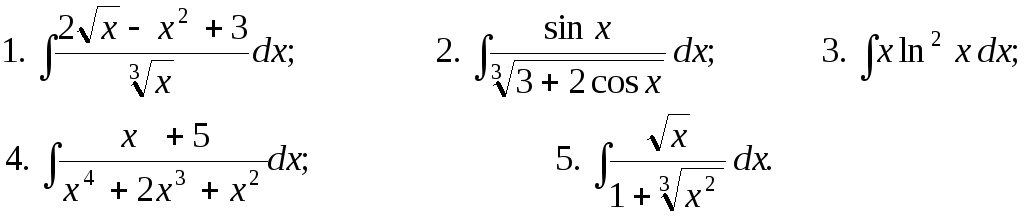
Задание 2. Вычислить площадь фигуры,
ограниченной линиями
![]() и
и
![]() .
.
Задание 3. Вычислить двойной интеграл,
область D изобразить на
чертеже.
![]() где
где
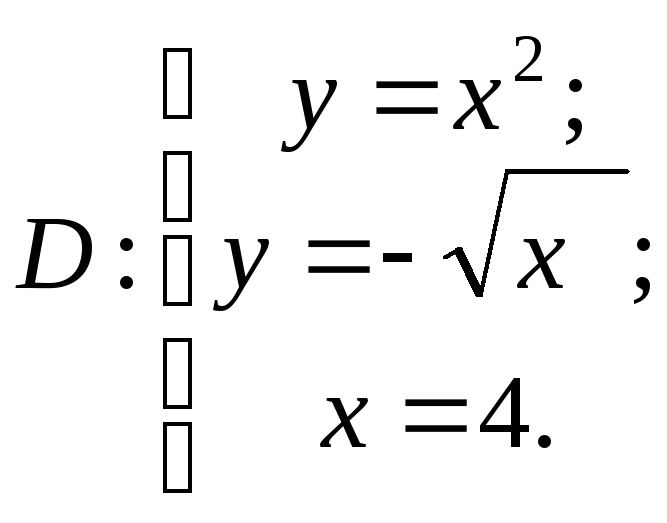
Задание 4. Задана функция
![]() и точка
и точка
![]() .
Найти: а) частные производные заданной
функции в точке
.
Найти: а) частные производные заданной
функции в точке
![]() ;
б) производную функции
;
б) производную функции
![]() в точке
в точке
![]() в направлении радиуса-вектора этой
точки; в) вычислить градиент функции
в направлении радиуса-вектора этой
точки; в) вычислить градиент функции
![]() в точке
в точке
![]() и сравнить его модуль со значением
производной, вычисленной в пункте б).
и сравнить его модуль со значением
производной, вычисленной в пункте б).
![]() .
.
Задание 5. Издержки фирмы зависят
от количества
![]() произведенных изделий А и от количества
произведенных изделий А и от количества
![]() произведенных изделий В в соответствии
с указанной в задании формулой. Найти,
сколько изделий А и В должна произвести
фирма, чтобы ее издержки были наименьшими.
произведенных изделий В в соответствии
с указанной в задании формулой. Найти,
сколько изделий А и В должна произвести
фирма, чтобы ее издержки были наименьшими.
![]()
Фирма может производить в совокупности не более 11 изделий в неделю, а изделий В должно быть не менее 3.
Задание 6. Получить линейную
зависимость
![]() методом наименьших квадратов по следующим
данным:
методом наименьших квадратов по следующим
данным:
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
3,8 |
4,8 |
3,3 |
1,3 |
1,8 |
Контрольная работа № 3
Вариант 5.
Задание 1. Найти неопределенные интегралы:
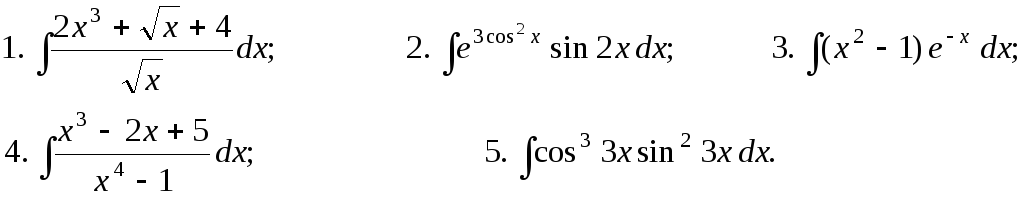
Задание 2. Вычислить объем тела,
образованного вращением вокруг оси
![]() фигуры, ограниченной линиями
фигуры, ограниченной линиями
![]() и
и
![]() .
.
Задание 3. Вычислить двойной интеграл,
область D изобразить на
чертеже.
![]() где
где
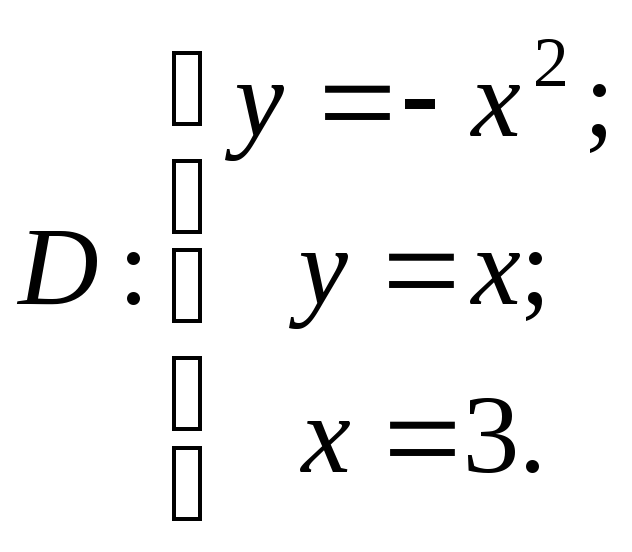
Задание 4. Задана функция
![]() и точка
и точка
![]() .
Найти: а) частные производные заданной
функции в точке
.
Найти: а) частные производные заданной
функции в точке
![]() ;
б) производную функции
;
б) производную функции
![]() в точке
в точке
![]() в направлении радиуса-вектора этой
точки; в) вычислить градиент функции
в направлении радиуса-вектора этой
точки; в) вычислить градиент функции
![]() в точке
в точке
![]() и сравнить его модуль со значением
производной, вычисленной в пункте б).
и сравнить его модуль со значением
производной, вычисленной в пункте б).
![]() .
.
Задание 5. Издержки фирмы зависят
от количества
![]() произведенных изделий А и от количества
произведенных изделий А и от количества
![]() произведенных изделий В в соответствии
с указанной в задании формулой. Найти,
сколько изделий А и В должна произвести
фирма, чтобы ее издержки были наименьшими.
произведенных изделий В в соответствии
с указанной в задании формулой. Найти,
сколько изделий А и В должна произвести
фирма, чтобы ее издержки были наименьшими.
![]()
Фирма может производить в совокупности не более 9 изделий в неделю, а изделий А должно быть не менее 4.
Задание 6. Получить линейную
зависимость
![]() методом наименьших квадратов по следующим
данным:
методом наименьших квадратов по следующим
данным:
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
4 |
5 |
3,5 |
1,5 |
2 |
Контрольная работа № 3
Вариант 6.
Задание 1. Найти неопределенные интегралы:
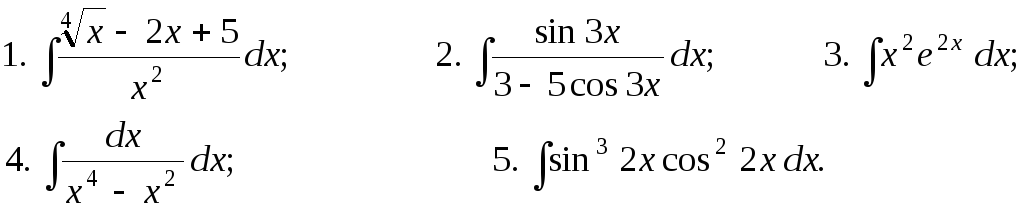
Задание 2. Вычислить длину дуги линии
![]() от
от
![]() до
до
![]() .
.
Задание 3. Вычислить двойной интеграл,
область D изобразить на
чертеже.
![]() где
где
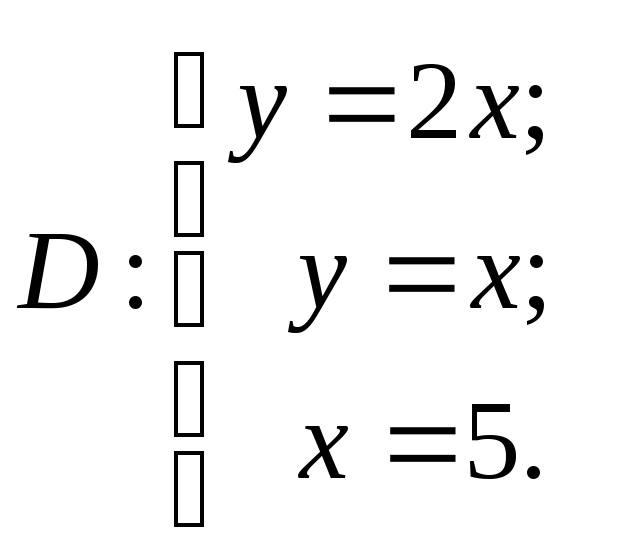
Задание 4. Задана функция
![]() и точка
и точка
![]() .
Найти: а) частные производные заданной
функции в точке
.
Найти: а) частные производные заданной
функции в точке
![]() ;
б) производную функции
;
б) производную функции
![]() в точке
в точке
![]() в направлении радиуса-вектора этой
точки; в) вычислить градиент функции
в направлении радиуса-вектора этой
точки; в) вычислить градиент функции
![]() в точке
в точке
![]() и сравнить его модуль со значением
производной, вычисленной в пункте б).
и сравнить его модуль со значением
производной, вычисленной в пункте б).
![]() .
.
Задание 5. Прибыль фирмы зависит от
количества
![]() и
и
![]() произведенного товара А и В соответственно
по указанной в задании формуле. Найти,
сколько изделий А и В должна произвести
фирма, чтобы получить наибольшую прибыль.
произведенного товара А и В соответственно
по указанной в задании формуле. Найти,
сколько изделий А и В должна произвести
фирма, чтобы получить наибольшую прибыль.
![]()
Фирма может произвести в неделю не более 5 единиц товара А и В в совокупности, а изделий В должно быть не менее 2.
Задание 6. Получить линейную
зависимость
![]() методом наименьших квадратов по следующим
данным:
методом наименьших квадратов по следующим
данным:
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
2,8 |
3,8 |
2,3 |
0,3 |
0,8 |
