5 Оценка точности по разностям двойных измерений

В геодезии часто приходится измерять большие группы однородных величин, причём каждую величину для контроля измеряют дважды.

5.1 Двойные равноточные измерения

Пусть однородные величины измерены равноточно дважды и получены результаты измерений:

Составим разности по формуле

.

Наиболее надёжные значения определяемых величин находим по формуле:

.

Для оценки точности используем разности .

1. При отсутствии систематических ошибок разности d_i можно рассматривать как истинные ошибки самих разностей, так как истинное значение разностей равно нулю ().

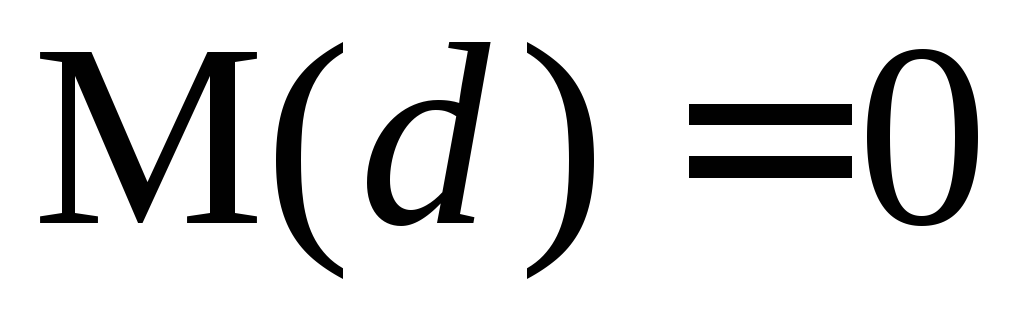Применяя к ряду формулу Гаусса , находим:

.

Тогда средняя квадратическая ошибка отдельного результата измерений будет определяться по формуле:

.

Оценка точности наиболее надёжных значений определяется по формуле:

.

2. Если в результатах измерений присутствуют систематические ошибки, то величина

существенно отличается от нуля.

В этом случае из каждой разности необходимо исключить остаточное влияние систематических ошибок, т. е. получить разности

.

Рассматривая разности  как уклонения от среднего , применяя формулу Бесселя, находим

.

Средние квадратические ошибки отдельного результата измерений и наиболее надёжных значений измеряемых величин находим по формулам:

,
.

Заметим, что в этом случае необходимо выполнить контроль вычислений по формулам

, где ; .

Для определения значимости отклонения от нуля применяют неравенство

,

где выбирают из таблиц Стьюдента по заданной вероятностии числу степеней свободы, а прикоэффициентt выбирают из таблиц интеграла вероятностей по заданной вероятности . Так, для, и неравенство  принимает вид:

.

Иногда применяют более жёсткий критерий обнаружения систематических ошибок

,

который получен, исходя из требования .

Оценку точности начинают с проверки условия  или . Если, например, неравенство  выполняется, то делают вывод о том, что систематическими ошибками можно пренебречь и оценку точности следует выполнять по формулам (5.4–5.5).

Если неравенство  не выполняется, делают заключение о том, что систематическими ошибками пренебрегать нельзя, необходимо обработку вести по формулам (5.7, 5.9, 5.10).

5.2 Двойные неравноточные измерения

Пусть каждая из однородных величин Х_i () измерена дважды и независимо, причём измерения в каждой паре равноточны, а пары между собой неравноточны. Известны весар_i результатов измерений. Получены разности d_i с весами .

Наиболее надёжные значения измеряемых величин находит по формуле .

Критерий обнаружения систематических ошибок имеет вид:

.

Если неравенство выполняется, то делают заключение о том, что систематическими ошибками можно пренебречь. Затем находят:

1. Среднюю квадратическую ошибку измерения с весом, равным единице,

   .

2. Средние квадратические ошибки наиболее надёжных значений

.

Если условие  не выполняется, то необходимо найти остаточное влияние систематических ошибок

и исключить его из каждой разности. Получают разности, свободные от влияния систематических ошибок

.

Оценка точности выполняется следующим образом:

1. Определяется средняя квадратическая ошибка измерения с весом, равным единице

   .

2. Вычисляются средние квадратические ошибки наиболее надёжных значений

.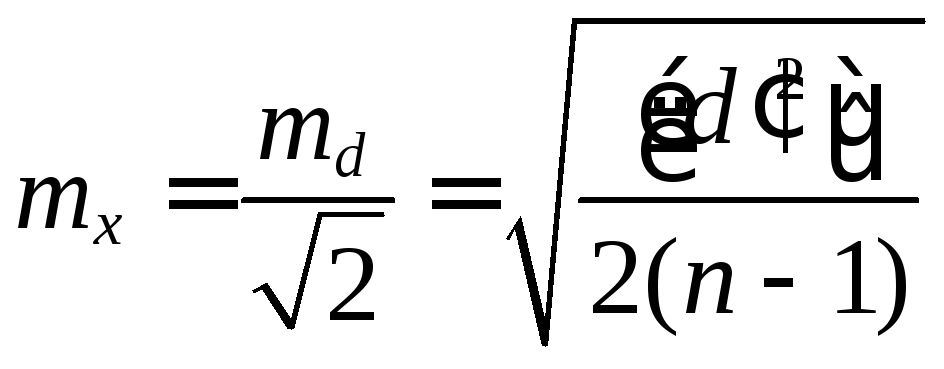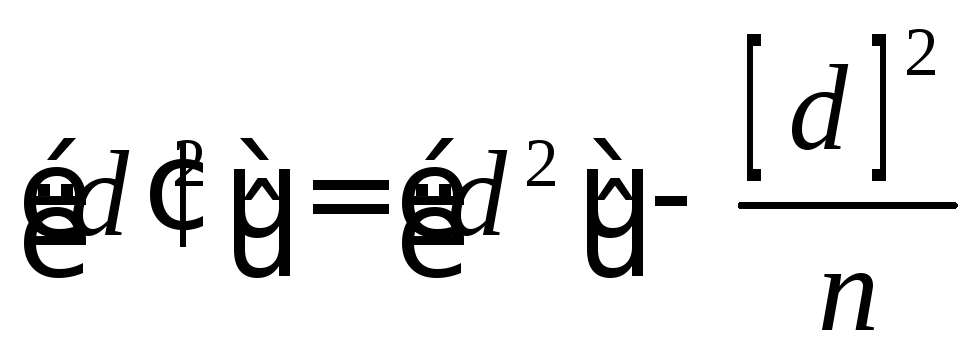