
Функція
.pdf
Розділ ІV „ВСТУП ДО МАТЕМАТИЧНОГО АНАЛІЗУ”
Функція 1. Поняття функції
Різноманітні процеси природи дають нам численні приклади явищ, в яких зміна одних величин приводить до зміни інших. Для вивчення того чи іншого явища треба встановити взаємозв’язок між величинами, які його описують, і дослідити його властивості. Такий взаємозв’язок у математиці задається за допомогою функції. Наведемо ряд прикладів.
Розглянемо дві змінні величини x та y з областями зміни X та Y відповідно ( X, Y – деякі числові множини).
Означення. Змінна y називається функцією змінної x, якщо кожному значенню x з її області зміни X за деяким правилом чи законом поставлено у
відповідність одне певне значення y Y.
При цьому x називається незалежною змінною або аргументом функції. Область зміни X незалежної змінної називається областю визначення функції.
Той факт, що y є функцією від x, записують так: y = f (x). Буквою f в цьому записі позначено закон відповідності між змінними x та y. Значення y0 Y змінної y, яке відповідає конкретному значенню x0 X аргумента, називають значенням функції
y = f (x) |
при |
x = x0 і позначають y0 = f (x0).
Множину всіх значень функції, яких вона набуває на елементах множини , називають областю зміни функції або множиною її значень. Область визначення та множину значень функції y = f (x) позначають відповідно ще й так: D(y) та E(y) або D( f ) та E( f ).
Далі нам доведеться, в основному, мати справу з областями визначення функцій двох типів. Якщо областю визначення функції є множина (або підмножина) натуральних чисел, таку функцію будемо називати функцією цілочисельного аргументу. У випадку, коли областю визначення функції є один або кілька проміжків числової осі, функцію називають функцією неперервного аргументу.
При одночасному розгляді кількох різних функцій використовують різні букви для позначення кожного із законів відповідності, наприклад: y = f (x), y = g(x), y =
F(x) |
і |
т.і. |
Замість |
y |
= |
f |
(x) |
часто |
пишуть |
y = y(x), позначаючи однією буквою і функцію, і закон відповідності.
Інколи в означенні поняття функції допускають, що кожному значенню x Х
відповідає не одне, а кілька значень y Y. В цьому випадку функцію y = f (x) називають багатозначною на відміну від визначеного вище поняття однозначної функції. Дві функції вважаються рівними або тотожними, якщо вони мають одну й ту ж область визначення і один закон відповідності.
2.Основні способи задання функцій
Щоб задати деяку функцію y = f (x), потрібно задати, по-перше, область визначення функції X і, по-друге, закон відповідності, за яким кожному дійсному
числу x ставиться у відповідність деяке дійсне число y.
Основними способами задання функцій є аналітичний, табличний та графічний способи.
1
При аналітичному способі задання функції закон відповідності між значеннями аргументу та значеннями функції подається у вигляді однієї або кількох
формул (аналітичних виразів). Наприклад, формула y=2x-xsinx, x ; задає на множині дійсних чисел деяку функцію.
Функція
задана на відрізку [– 1, 2] за допомогою трьох формул.
Іноді функцію задають аналітично і не вказують її область визначення. В цьому випадку під областю визначення такої функції розуміють множину всіх дійсних значень аргументу, для яких аналітичний вираз має зміст і в процесі проведення всіх необхідних обчислень за цим виразом одержуються тільки дійсні числа. Наприклад, областю визначення функції y = 
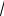 x2 2x 3 4x 1 буде множина
x2 2x 3 4x 1 буде множина
тих значень аргументу x, для яких виконується умова x2 – 2x – 3 , тобто множина
D(y) = ]– ; – 1] [3; + [.
Табличний спосіб задання функції полягає в тому, що для виписаних у певному порядку значень аргументу x1, x2, ..., xn вказують відповідні значення функції y1, y2, ..., yn.
Такими є, наприклад, таблиці тригонометричних функцій, таблиці логарифмів, таблиці результатів фізичних експериментів, в яких визначають залежність однієї величини від другої і т.і.
x |
X1 |
x2 |
... |
xn |
Існують |
методи, які |
дозволяють |
y |
Y1 |
y2 |
... |
yn |
наближено знаходити значення функції, що |
||
відповідають |
проміжним |
значенням |
|||||
аргументу, відсутнім у таблиці (так звані методи інтерполяції).
У практиці фізичних досліджень широко використовується графічний спосіб задання функції. Для з’ясування суті цього способу введемо спочатку поняття
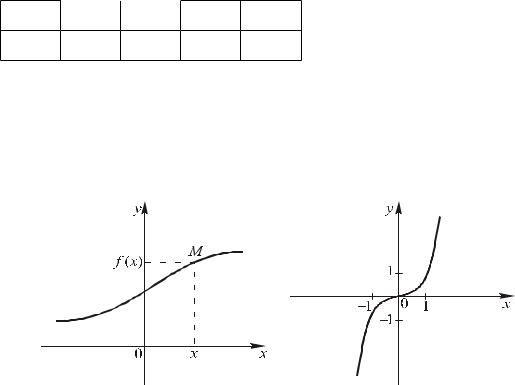
графіка функції y = f (x) з областю визначення x X. В декартовій прямокутній системі координат Оxy розглянемо множину X точок на осі Оx, яка відповідає
області визначення функції. Кожній парі (х, у), де x X y = f (x), поставимо у
Рис. 1 |
Риc. 2 |
2

відповідність точку М площини з координатами (x, f (x)). Сукупність всіх точок площини, абсциси яких є значеннями аргументу функції, а ординати – відповідними значеннями функції, називається графіком даної функції (рис 1).
Для переважної більшості функцій, які розглядаються у нашому курсі, областю визначення є один або кілька проміжків, а графіком – деяка крива.
Наприклад, графіком функції y = x3, x ]– , + ] є кубічна парабола (рис 2). Одночасно рівняння y = x3 буде рівнянням цієї параболи в системі координат Оxy. Проте зустрічаються випадки, коли графік функції, визначеної на деякому проміжку, важко назвати кривою. Прикладом такої функції може служити функція
Діріхле :
1,якщох раціональнечисло, y .
0,якщох ірраціональнечисло.
Якщо в прямокутній системі координат на площині задана деяка сукупність точок M(x; y), причому ніякі дві з цих точок не лежать на одній прямій, паралельній осі Оy, то ця сукупність точок визначає цілком певну однозначну функцію y = f (x). Значеннями аргументу функції є абсциси точок, значеннями функції – відповідні ординати; сама сукупність точок є графіком цієї функції.
Графічним способом задання функції широко користуються при дослідженнях, пов’язаних з використанням приладів-самозаписувачів (осцилограф, барограф, електрокардіограф і т.і. ). Крива, що її виписує прилад, задає деяку функцію, властивості якої треба знати для вивчення того чи іншого процесу.
3. Поняття про обернену функцію
Нехай однозначна функція y = f (x) задана на відрізку a, b і множиною значень цієї функції є деякий відрізок c, d на осі Оy.
Нехай далі кожному y c, d відповідає тільки одне x a, b для якого f (x) = у. Тоді на відрізку c, d визначена однозначна функція, яка кожному y з відрізка c, d
ставить у відповідність те значення x відрізка a, b , для якого f (x) = y. Ця функція позначається символом x = f –1(y) і називається оберненою для функції y = f (x). Очевидно, що оберненою для функції x = f –1(y) буде сама функція y = f (x).Тому функції y = f (x) та x = f – 1(y) називають взаємно оберненими. Наприклад, для функції
y = 2x на будь-якому проміжку x a b оберненою буде функція x= 12 y, визначена на
відрізку [2a, 2b]. Вигляд оберненої функції ми знайшли, розв’язавши рівняння y=2x відносно x.
Графіки функцій y = f (x) та x = f (y) складаються з одних і тих же точок координатної площини, тобто збігаються. Якщо ж перейти в оберненій функції до
звичних позначень (аргумент – x, функція – y), тобто замість x = f (y) розглянути функцію y = f (x), то графіки функцій y = f (x) та y = f x вже будуть відрізнятись, а
3

саме, графік функції y = f x буде симетричним з графіком функції y = f (x) відносно бісектриси y = x першого – третього координатних кутів (рис 3).
Умови існування та деякі властивості оберненої функції будуть розглянуті далі.
Рис 3
4. Елементарні функції
При побудові класу елементарних функцій використовуються так звані
основні елементарні функції, до яких відносяться: степенева функція y = x ( – дійсне число); показникова функція y = ax (a > 0, a 1 – дійсне число);
логарифмічна функція y = loga x (a > 0, a 1 – дійсне число); тригонометричні функції y = sin x, y = cos x, y = tg x, y = ctg x;
обернені тригонометричні функції y = arcsin x, y = arccos x, y = arctg x, y = arcctg x. Ці функції, їх основні властивості розглядаються в шкільному курсі математики. На рис 4 – 23 зображено ескізи графіків деяких основних елементарних функцій.
Основні елементарні функції, їх графіки та властивості І. Степенева функція у = хп,
де х – незалежна зміна (аргумент), п – стала.
а). Лінійна функція y = kx + b.
Y |
|
|
|
|
y = kx + b |
b |
α |
|
O |
tg = k |
X |
|
|
1.Область визначення – множина всіх дійних чисел: х R .
2.Множина значень – множина всіх дійсних чисел: y R .
4

3.Функція y = kx + b не парна, ні непарна.
4.Функція зростає при k > 0 і спадає при k < 0.
5.Графіком функції y = kx + b є пряма лінія для якої k = tg . Число k називається кутовим коефіцієнтом прямої і дорівнює тангенсу кута, який пряма утворює з додатнім напрямом осі ОХ.
Число b дорівнює величині відрізка, який пряма y = kx + b відтинає на осі OY.
б). Функція у = х2.
Y 
у = х2
1
-1 О |
1 |
Х |
1.Область визначення – множина всіх дійсних чисел: х R .
2.Множина значень – всі невід’ємні числа: y > 0.
3.Функція у = х2 парна: у(–х) = (–х)2 = х2 = у(х).
4.Функція у = х2 зростає при x > 0, спадає при x < 0.
5.Графіком функції є парабола.
6.Всі властивості, наведені для функції у = х2, мають місце для функції у = хп, де п
– парне число.
в). Функція у = х3.
1.Область визначення – множина всіх дійсних чисел: х R .
2.Множина значень – множина всіх дійсних чисел: у R .
3.Функція у = х3 парна: у(–х) = (–х)3 = –х3 = –у(х).
|
Y |
|
|
|
у = х3 |
|
1 |
|
- |
О 1 |
Х |
1 |
||
|
- |
|
|
1 |
|
4.Функція зростає на всій області визначення.
5.Графіком функції є кубічна парабола.
6.Всі властивості, наведені для функції у = х3, мають місце для функції у = хп, де п
– непарне число.
г). Функція y 
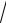 x.
x.
5
Y 
y 
 x.
x.
1
|
|
|
О 1 |
Х |
|
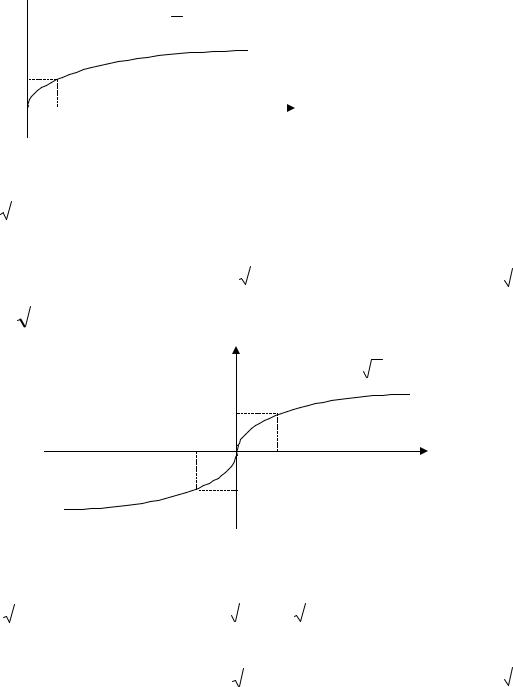
1.Область визначення – невід’ємні числа: х [0; + ).
2.Множина значень – невід’ємні числа: y [0; + ).
3. Функція y x |
ні парна, ні непарна. |
4.Функція зростає на всій області визначення.
5.Графік функції зображено на рисунку.
6. Всі властивості, наведені для функції y |
x, мають місце для функції y n |
|
, |
||
x |
|||||
де п – парне. |
|
|
|
|
|
д). Функція y 3 |
x |
|
|
|
|
Y |
y 3 |
x |
|
||
1 |
|
|
-1 |
1 |
|
О |
Х |
|
-1 |
|
|
1.Область визначення – множина всіх дійсних чисел: х R .
2.Множина значень – множина всіх дійсних чисел: у R .
3. |
Функція y 3 x |
непарна: y( x) 3 |
x 3 |
|
. y(x) |
|
|||
x |
|
||||||||
4. |
Функція зростає на всій області визначення. |
|
|
|
|
||||
5. |
Графік функції зображено на рисунку. |
|
|
, мають місце для функції y n |
|
|
|||
6. |
Всі властивості, наведені для функції y 3 |
|
x |
x |
, |
||||
де п – непарне.
6
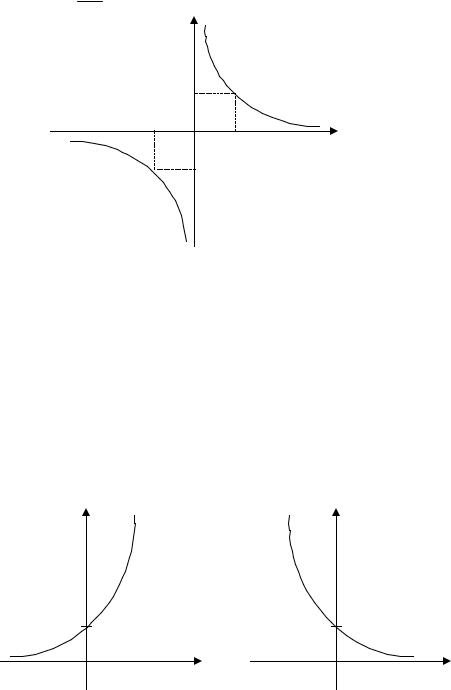
ж). Функція y 1 . |
|
|
|
|
|
1. |
x |
|
|
|
|
Область визначення: х (– ; 0) (0; + ). |
|
|
|||
2. |
Множина значень: y (– ; 0) (0; + ). |
|
|
||
|
y( x) 1 |
1 |
y(x) |
|
|
|
x |
x |
Y |
|
|
|
|
|
1 |
|
|
|
|
-1 |
1 |
|
|
|
|
|
О |
Х |
|
|
|
|
-1 |
|
|
3. |
Функція непарна: |
|
. |
|
|
4. |
Функція спадає на всій області визначення. |
|
|
||
5. |
Графіком функції є гіпербола. |
|
|
|
|
ІІ. Показникова функція у = ах, |
|
|
|
|
|
де основа a – стала (a > 0, a 1), x – аргумент (незалежна змінна). |
|||||
1. |
Область визначення – множина всіх дійсних чисел: х R . |
||||
2. |
Множина значень: у (0; + ) . |
|
|
|
|
3. |
Функція ні парна, ні непарна. |
|
|
|
|
4. |
Функція у = ах зростає, якщо a > 1 і спадає, якщо 0 < a < 1. |
||||
5. |
Графік функції у = ах має асимптоту у = 0 (вісь Ох). |
|
|||
Y |
|
Y |
|
|
у = ах; a > 1 |
|
у = ах; 0 < a < 1 |
1 |
|
1 |
|
О |
Х |
О |
Х |
6. Графік функції у = ах проходить через т. (0; 1).
7
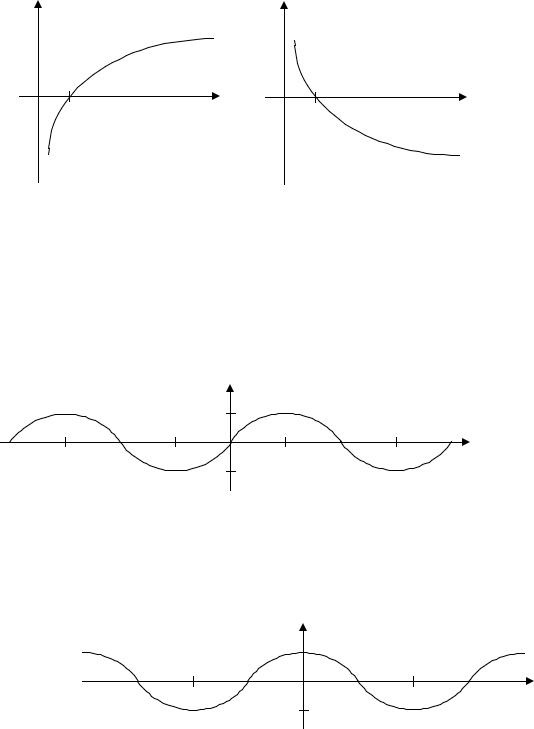
ІІІ. Логарифмічна функція y = loga x.
1.Область визначення – всі додатні числа: х (0; + ).
2.Множина значень – множина всіх дійсних чисел: у R .
Y |
у = loga |
x; a > 1 |
Y |
|
|
у = loga |
x; 0 < a < 1 |
||
|
|
|
1 |
|
|
1 |
О |
Х |
О |
Х |
3.Функція ні парна, ні непарна.
4.Функція y = loga x зростає, якщо a > 1 і спадає, якщо 0 < a < 1.
5.Графік функції y = loga x має асимптоту х = 0 (вісь Оу).
6.Графік функції y = loga x проходить через т. (1; 0).
IV. Тригонометричні функції a). y = sin x
|
|
|
Y |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
–3π/2 |
–π |
– π/2 |
О |
π/2 |
π |
3π/2 |
Х |
1. |
|
|
|
–1 |
|
|
|
|
Область визначення – множина всіх дійсних чисел: х R . |
|
|||||||
2. |
Множина значень: –1 у 1 . |
|
|
|
|
|
||
3. |
Функція y = sin x непарна: y(–х) = sin (–x) = – sin x = –у(x). |
|
||||||
4. |
Функція y = sin x періодична, Т = 2π. |
|
|
|
||||
б). y = cos x |
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1. |
–3π/2 |
–π |
– π/2 |
О |
π/2 |
π |
3π/2 |
Х |
Область визначення – множина всіх дійсних чисел: |
х R . |
|
||||||
2. |
Множина значень: –1 |
у 1 . |
|
–1 |
|
|
|
|
|
|
|
|
|
|
|||
3. |
Функція y = cos x парна: y(–х) = cos (–x) = cos x = у(x). |
|
|
|||||
4. |
Функція y = cos x періодична, Т = 2π. |
|
|
|
|
|
||
8
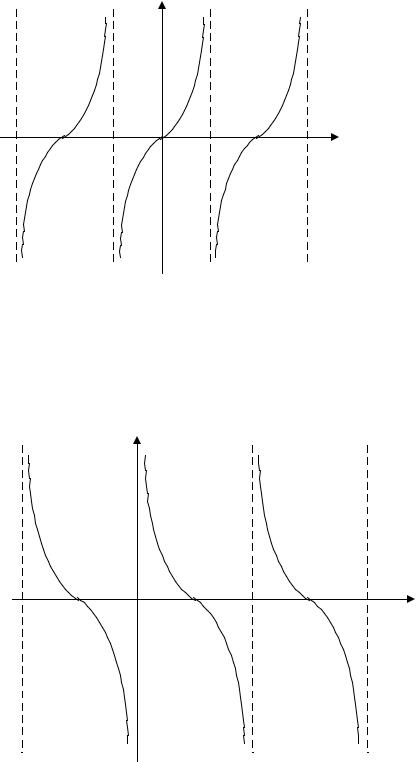
в). y = tg x |
|
|
|
|
|
|
|
||
|
1. |
Область визначення: |
|
|
|
. |
|
||
|
2. |
Множина значень – множина всіх дійсних чисел: у R . |
|||||||
|
3. |
Функція y = tg x непарна: y(–х) = tg (–x) = – tg x = –у(x). |
|||||||
|
4. |
Функція y = tg x зростає на всій області визначення. |
|||||||
|
5. |
Функція має вертикальні асимптоти м |
x |
|
n, n Z |
||||
|
2 |
||||||||
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–3π/2 |
–π |
–π/2О |
π/2 |
|
π |
|
|
|
|
3π/2 |
|
|
x |
|
|
|
Х |
|
|
|
|
|
n, n Z |
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
|
6. Функція y = tg x періодична Т = π. |
|
|
|
|||||
г). y = сtg x |
|
|
|
|
|
|
|
||
|
|
|
|
Y |
|
|
|
|
|
|
|
–π |
–π/2 |
О |
π/2 |
π |
3π/2 |
Х |
|
1. |
Область визначення: х π п, п Z . |
|
|
|
|||||
2. Множина значень – множина всіх дійсних чисел: у R . |
|||||||||
3. |
Функція y = сtg x непарна: y(–х) = сtg (–x) = – сtg x = –у(x). |
||||||||
9
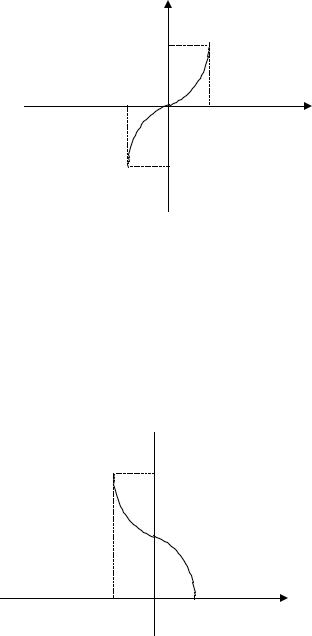
4.Функція спадає на всій області визначення.
5.Функція має вертикальні асимптоти: х π п, п Z .
6.Функція y = сtg x періодична Т = π.
V. Обернені тригонометричні функції.
а). у = arcsin x
Оберненою тригонометричною функцією у = arcsin x називається взята на
|
Y |
|
|
|
; |
|
|
|
|
2 |
2 |
|
|||
|
π/2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
-1 |
|
О |
1 |
|
||
|
|
|
Х |
||||
|
|
|
–π/2 |
|
|
||
відрізку |
величина у, синус якої дорівнює х. |
||||||
1.Область визначення: –1 х 1 .
2.Множина значень: 2 x 2.
3.Функція y = arcsin x непарна: y(–х) = arcsin (–x) = –arcsin x = –у(x).
4.Функція зростає на всій області визначення.
б). у = arccos x
Y 
π
π/2
-1 |
О 1 |
Х |
Оберненою тригонометричною функцією у = arccos x називається взята на відрізку [0; π] величина у, косинус якої дорівнює х.
1.Область визначення: –1 х 1 .
2.Множина значень: y π .
10
