
- •Модель ідеального перемішування Характеристика моделі
- •Диференціальне рівняння моделі
- •Розв'язання диференціального рівняння моделі
- •Умови фізичної реалізованості моделі ідеального перемішування
- •Модель ідеального витіснення Характеристика моделі
- •Диференціальне рівняння моделі
- •Розв'язання диференціального рівняння моделі
- •Умови фізичної реалізованості моделі ідеального витіснення
- •Коміркова модель Характеристика моделі
- •Математичний опис коміркової моделі
- •Розв'язання системи рівнянь коміркової моделі
- •Застосування коміркової моделі
- •Дифузійна модель Характеристика моделі
- •Диференціальне рівняння однопараметричної дифузійної моделі
- •Розв’язання диференціального рівняння моделі
- •Застосування дифузійної моделі
- •Комбіновані моделі
- •Об'єкт, що поєднує зони ідеального перемішування й байпасування
- •Об'єкт, що поєднує ділянки ідеального перемішування й застійної зони
- •Тема лекційного заняття 3. Описання структури моделей у апаратах безперервної дії. Дифузійна та коміркова математичні моделі.
Диференціальне рівняння моделі
Для складання математичного опису
моделі ідеального витіснення виділимо
й розглянемо елементарний об’єм зони
потоку витіснення (див. рис. 2.8) об'ємом
![]() ,
довжиною
,
довжиною![]() й перерізом
й перерізом![]() ,
що дорівнює одиниці (
,
що дорівнює одиниці ( ![]() ).
).
Вхідний і вихідний потоки для розглянутого
![]() -го
елементарного об’єму відповідно до
рівняння (2.2-1) будуть
-го
елементарного об’єму відповідно до
рівняння (2.2-1) будуть
![]() , (2.2-13а)
, (2.2-13а)
![]() , (2.2-13б)
, (2.2-13б)
д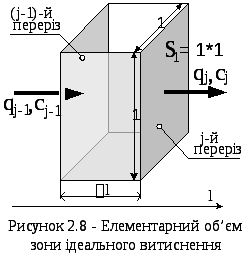 е
е![]() і
і![]() ‑ потоки (кількості речовини) на вході
й виході елементарного
‑ потоки (кількості речовини) на вході
й виході елементарного![]() -го
об’єму, тобто в
-го
об’єму, тобто в![]() -му
і
-му
і![]() -му
перерізах;
-му
перерізах;![]() ,
,![]() ‑ концентрація на вході й на виході
елементарного
‑ концентрація на вході й на виході
елементарного![]() -го
об’єму;
-го
об’єму;![]() — площа перерізу зони ідеаль-ного
витіснення;
— площа перерізу зони ідеаль-ного
витіснення;![]() — середня лінійна швидкість потоку
(для проточних систем вважається, що
— середня лінійна швидкість потоку
(для проточних систем вважається, що![]() зберігає середнє значення в усій зоні
витіснення).
зберігає середнє значення в усій зоні
витіснення).
Аналогічно, як і в випадку ідеального
перемішування, кількість речовини
![]() ,
яка буде акумулюватися в елементарному
об'ємі
,
яка буде акумулюватися в елементарному
об'ємі![]() при порушенні режиму рівноваги, тобто
коли
при порушенні режиму рівноваги, тобто
коли![]() не дорівнює
не дорівнює![]() ,
можна виразити рівнянням (з урахуванням
того, що
,
можна виразити рівнянням (з урахуванням
того, що![]() )
)
![]() .
(2.2-14)
.
(2.2-14)
Якщо розділити величину збільшення
кількості речовини
![]() на об'єм
на об'єм![]() ,
то одержимо вираз для опису зміни
концентрації в розглянутому
,
то одержимо вираз для опису зміни
концентрації в розглянутому![]() -му
елементарному об’ємі
-му
елементарному об’ємі![]() у
вигляді
у
вигляді
![]() , (2.2-15)
, (2.2-15)
де
![]() — різниця концентрацій у суміжних
— різниця концентрацій у суміжних![]() -му
і
-му
і![]() -му
об’ємах;
-му
об’ємах;![]() — зміна концентрації в елементарному
об’ємі;
— зміна концентрації в елементарному
об’ємі;![]() — значення концентрації до початку
збурювання;
— значення концентрації до початку
збурювання;![]() — концентрація у будь-який момент часу
(змінна величина);
— концентрація у будь-який момент часу
(змінна величина);![]() (враховуючи, шо
(враховуючи, шо![]() ).
Оскільки
).
Оскільки![]() не залежить від часу
не залежить від часу![]() ,
рівняння (2.2-15) можна переписати у вигляді
,
рівняння (2.2-15) можна переписати у вигляді
![]() . (2.2-16)
. (2.2-16)
У результаті диференціювання правої й
лівої частин рівняння (2.2-16) за часом і
граничного переходу при
![]() одержуємо
одержуємо
![]() , (2.2-17)
, (2.2-17)
або остаточно
![]() . (2.2-18)
. (2.2-18)
Рівняння (2.2-17) описує зміна концентрації
![]() в елементарному
в елементарному![]() -му
об'ємі
-му
об'ємі![]() зони ідеального витиснення, але оскільки
режим потоку поршневий, то рівняння
справедливе і для всього потоку. Тому
диференціальне рівняння моделі ідеального
витіснення в загальному вигляді записують
так:
зони ідеального витиснення, але оскільки
режим потоку поршневий, то рівняння
справедливе і для всього потоку. Тому
диференціальне рівняння моделі ідеального
витіснення в загальному вигляді записують
так:
![]() . (2.2-19)
. (2.2-19)
Таким чином, математична модель режиму
ідеального витіснення являє собою
диференціальне рівняння в частинних
похідних, оскільки основна змінна
процесу — концентрація![]() — змінюється в часі і у просторі. Як
відомо,це модель із розподіленими
параметрами.
— змінюється в часі і у просторі. Як
відомо,це модель із розподіленими
параметрами.
Якщо замість середньої лінійної швидкості
потоку
![]() в рівняння (2.2-19) підставити її значення
в рівняння (2.2-19) підставити її значення![]() ,
то воно набуває такого вигляду
,
то воно набуває такого вигляду
![]() . (2.2-20)
. (2.2-20)
Рівняння (2.2-20) відображає розподіл
речовини (концентрації) у потоці з
гідродинамічною структурою ідеального
витиснення. Аналогічне за формою рівняння
може бути також виведене, якщо розглянути
зміну іншої характерної змінної,
наприклад, температури
![]() ,
у потоці теплоносія зі структурою
ідеального витіснення. Тоді зміну
,
у потоці теплоносія зі структурою
ідеального витіснення. Тоді зміну![]() в потоці теплоносія за рахунок
гідродинаміки можна зобразити так:
в потоці теплоносія за рахунок
гідродинаміки можна зобразити так:
![]() , (2.2-21)
, (2.2-21)
де
![]() — теплоємність речовини потоку
теплоносія;
— теплоємність речовини потоку
теплоносія;![]() — температура у будь-якій точці зони
ідеального витіснення. Модель у вигляді
рівняння (2.2-21) часто використовується
для опису гідродинаміки потоку теплоносіїв
у теплообмінних апаратах, що працюють
за принципом витіснення.
— температура у будь-якій точці зони
ідеального витіснення. Модель у вигляді
рівняння (2.2-21) часто використовується
для опису гідродинаміки потоку теплоносіїв
у теплообмінних апаратах, що працюють
за принципом витіснення.
Розв'язання диференціального рівняння моделі
Для об'єкта, структура потоку в якому відповідає моделі ідеального витіснення, розв'язки диференціального рівняння (2.2-20), відповідні стандартним сигналам, будуть такі:
при ступінчастому стандартному сигналі на вході (перехідна функція)
![]() ; (2.2-22)
; (2.2-22)
при імпульсному стандартному сигналі на вході (функція ваги)
![]() . (2.2-23)
. (2.2-23)
Перехідна й імпульсна перехідна
характеристики, побудовані відповідно
до виразів для перехідної (2.2-22) і
імпульсної перехідної (2.2-23) функцій,
подані на рис. 2.9аі 2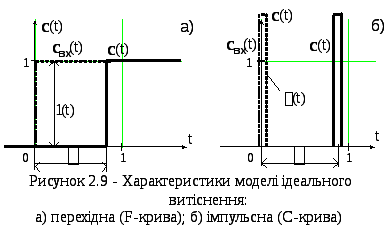 .9бвідповідно. Із графіків можна побачити,
що вихідні криві повторюють за формою
вхідні впливи, але тільки зі зміщенням
за часом на величину
.9бвідповідно. Із графіків можна побачити,
що вихідні криві повторюють за формою
вхідні впливи, але тільки зі зміщенням
за часом на величину![]() .
Звідси випливає практичний результат,
яким користуються при експериментальному
вивченні невідомої структури потоку в
апараті: якщо при стандартних ступінчастому
або імпульсному вхідних сигналах на
виході потоку реєструється їхнє
повторення зі зміщенням за часом, то
такий потік відповідає моделі ідеального
витіснення.
.
Звідси випливає практичний результат,
яким користуються при експериментальному
вивченні невідомої структури потоку в
апараті: якщо при стандартних ступінчастому
або імпульсному вхідних сигналах на
виході потоку реєструється їхнє
повторення зі зміщенням за часом, то
такий потік відповідає моделі ідеального
витіснення.
