Лекція 5

1. Модель ідеального перемішування Характеристика моделі

Модель ідеального перемішування являє собою ідеалізований потік і є теоретичною моделлю. Згідно із цією моделлю припускається, що потік, який надходить в апарат, миттєво розподіляється по всьому об'єму внаслідок повного (ідеального) перемішування частинок середовища. При цьому концентрація розподіленої речовини в усіх точках апарата і у вихідному потоці з нього однакова. Схематичне зображення, що пояснює ідею моделі ідеального перемішування, наведене на рис. 2.4.

Диференціальне рівняння моделі

В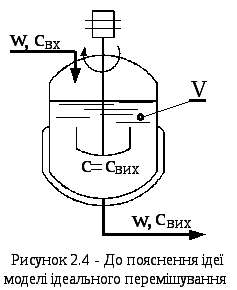иведемо математич-ну залежність, що описує розподіл концентрації в апараті з об'ємом зони ідеального перемішуван-няв часі.

Кількість речовини (масовий потік) у будь-якому місці системи в загальному випадку можна представити як добуток

, (2.2-1)

де — об'ємна швид-кість потоку, що надхо-дить у зону ідеального перемішування і виходить з неї (для проточних систем припускається, щозберігає постійне значення у будь-якому місці),м³/с;‑ концентрація речовини в потоці в будь-якій точці об'єму апарата,моль/м³.

З урахуванням цього для об'єкта (рис. 2.4) вхідний і вихіднийпотоки будуть

, (2.2-2а)

, (2.2-2б)

де ,— концентрація речовини в потоці відповідно на вході й виході апарата.

В усталеному режимі, коли , справедлива рівність, і накопичення маси речовини в апараті не відбувається, тобто скільки речовини надходить в апарат, стільки з нього і виходить у будь-який момент часу. Однак у загальному випадку може виникнути, наприклад, збурювання за складом потоку на вході. Припустимо, що вхідна концентраціяу якийсь момент часу збільшилася. При цьому рівновага, що встановилася раніше, порушується, і рівність вхідного й вихідного потоків не дотримується. У результаті в апараті за часбуде акумулюватися деяка кількість речовини, що може бути визначена з виразу в інтегральній формі:

. (2.2-3)

Перетворимо рівняння (2.2-3), розділивши обидві його частини на (об'єм реактора) і підставивши замість величин,їх вирази з (2.2-2):

. (2.2-4)

Ліва частина рівняння (2.2-4) — це зміна кількості речовини, віднесена до одиниці об'єму, тобто зміна концентрації , яку можна записати у вигляді

, (2.2-5)

де — концентрація у будь-який момент часу (змінна величина);— величина концентрації до моменту збурювання. Тоді рівняння (2.2-4) з урахуванням (2.2-5)

. (2.2-5)

Отриманий вираз являє собою математичний опис моделі ідеального перемішування в інтегральній формі. У результаті диференціювання рівняння (2.2-5) отримаємо закон зміни концентрації в часі в розглянутому потоці або математичний опис моделі ідеального перемішування в диференціальній формі:

. (2.2-6)

Відношення (зворотне записаному у формулі (2.2-6)) характеризує середній час знаходження частинок потоку у зоні ідеального перемішування; його прийнято називатичасом перебуваннячастинок в апараті й позначати грецькою літерою(тау). Час перебування є основним параметром моделі ідеального перемішування, який визначається експериментально або розрахунковим шляхом. Диференціальне рівняння моделі ідеального перемішування часто записують з урахуванням параметра:

. (2.2-7)

За видом моделі ідеального перемішування — за видом рівнянь (2.2-6) або (2.2-7) — видно, що це модель із зосередженими параметрами, оскільки основна змінна змінюється тільки в часі. Рівняння (2.2-6) у літературі іноді зустрічається і у такому вигляді:

. (2.2-8)

Рівняння (2.2-8) відображає розподіл концентрації речовини в об'ємі зони з гідродинамічною структурою ідеального перемішування. Аналогічне за формою рівняння може бути отримане, якщо розглянути зміну іншої характерної змінної потоку, наприклад, температури , у потоці теплоносія зі структурою ідеального перемішування. Тоді рівняння (2.2-8) набуде вигляд

, (2.2-9)

де — теплоємність речовини потоку;,— температура на вході й у будь-якій точці зони ідеального перемішування відповідно.

Рівняння (2.2-9) характеризує розподіл температури в потоці з гідродинамічною структурою ідеального перемішування.