фа состояний (см. рис. 2.15). Система алгебраических уравнений
для финальных вероятностей имеет вид λp1 = µp2 , Добавляя ус-
µp2 = λp1.
ловие нормировки p1 + p2 =1, получим p1 = λ µ+ µ и p2 = λ λ+ µ .
3.СТАЦИОНАРНЫЙ СЛУЧАЙНЫЙ ПРОЦЕСС
ИЕГО ПРЕОБРАЗОВАНИЕ ЛИНЕЙНОЙ СТАЦИОНАРНОЙ
СИСТЕМОЙ
3.1. Действительная форма спектрального разложения стационарного случайного процесса
Рассмотрим элементарный случайный процесс
ξ(t) = Acosωt + Bsin ωt , |
(3.1) |
для которого случайные величины A и B имеют нулевые математические ожидания и равные дисперсии так, что
M[A] = M[B] = 0 и M[A2 ] = M[B2 ] = d . |
(3.2) |
Определим, какие дополнительные ограничения нужно наложить на случайные величины A и B , чтобы элементарный случайный процесс (3.1) был с тационарным в широком смысле, т.е. чтобы его ковариационная функция Kξ (t1,t2 ) зависела только от раз-
ности моментов времени |
t2 −t1 = τ. Случайные |
величины |
ξ(t1) = Acosωt1 + Bsin ωt1 и |
ξ(t2 ) = Acosωt2 + Bsin ωt2 , |
которые |
являются значениями процесса (2.8) в моменты времени t1 и t2 ,
имеют нулевые математические ожидания, поэтому их ковариация равна математическому ожиданию их произведения:
|
|
|
|
Kξ (t1,t2 ) = M[ξ(t1)ξ(t2 )] . |
|
(3.3) |
|||||||
Преобразуем |
произведение |
этих |
случайных |
|
величин: |
||||||||
ξ(t )ξ(t |
2 |
) = A2 cos |
ωt |
cosωt |
2 |
+ AB cosωt sin ωt |
2 |
+ ABsin ωt |
cosωt |
2 |
+ |
||
1 |
|
1 |
|
|
1 |
|
1 |
|
|
||||
+ B2 sin ωt1 sin ωt2 . Далее, применяя формулу для синуса суммы двух углов, придём к выражению
71
ξ(t )ξ(t |
2 |
) |
= A2 cosωt cosωt |
2 |
+ |
|
|
|
||
1 |
|
|
|
1 |
|
|
|
(3.4) |
||
+ B2 sin ωt |
sin ωt |
|
+ ABsin ω(t +t |
|
). |
|||||
2 |
2 |
|
||||||||
|
|
1 |
|
|
1 |
|
|
|
||
Подставляя (3.4) в (3.3) и вспоминая формулу для косинуса |
||||||||||
разности двух углов, получим с учетом (3.2) |
|
|
|
|||||||
Kξ (t1,t2 ) = d cosω(t2 −t1) + M[AB]sin ω(t1 +t2 ) . |
(3.5) |
|||||||||
Если M[AB] = 0 , то |
|
|
|
|
|
|
|
|
|
|
Kξ (t1,t2 ) = d cosω(t2 −t1) . |
|
|
(3.6) |
|||||||
Таким образом, для того чтобы элементарный случайный процесс (3.1) был стационарным, достаточно к условию (3.2) добавить условие некоррелированности случайных величин A и B , т.е. условие M [AB]= 0 .
Пусть теперь случайный процесс есть конечная сумма элементарных случайных процессов вида (3.1) (см. также формулу(2.8)):
n |
|
ξ(t) = mξ + ∑(Al cosωlt + Bl sin ωlt) . |
(3.7) |
l=1
Круговые частоты ω1,ω2 ,...ωn выбраны произвольно. Случайные величины Al , Bl (l =1,2,...n) удовлетворяют условиям
M[Al ] = M[Bl ] = 0 , M[Al2 ] = M[Bl2 ] = dl ,
M[Al Ak ] = 0,l ≠ k , M[Bl Bk ] = 0,l ≠ k , M[Al Bk ] = 0 ,
при выполнении которых слагаемые в сумме (3.7) некоррелированны. Ковариационная функция суммы некоррелированных слагаемых равна сумме ковариационных функций (3.6) этих слагаемых:
n |
|
Kξ (t1,t2 ) = ∑dl cosωl (t2 −t1) . |
(3.8) |
l=1
Таким образом, ковариационная функция случайного процесса (3.7) зависит только от разности t2 −t1 , что говорит о стационар-
ности этого процесса. Обозначая разность t2 −t1 = τ, перепишем
(3.8) в виде
n |
|
Kξ(t1,t2 ) = ∑dl cosωl τ . |
(3.9) |
l=1
72
Выберем теперь спектр частот ω1,ω2 ,...ωn случайного процесса (3.7) специальным образом:
ωl = |
πl |
(l =1,2,...) . |
(3.10) |
|
T |
|
|
Этот дискретный спектр частот процесса будет бесконечным и
∆ω = ωl+1 −ωl |
= |
π |
, |
(3.11) |
|
||||
|
|
T |
|
|
где T – положительное число. Формулы (3.7) и (3.9) принимают |
||||
вид |
|
|
|
|
∞ |
|
|
|
|
ξ(t) = mξ + ∑(Al cosωlt + Bl sin ωlt) , |
(3.12) |
|||
l=1 |
|
|
|
|
∞ |
|
|
|
|
Kξ (τ) = ∑dl cosωl τ . |
(3.13) |
|||
l=1 |
|
|
|
|
Предположим, что дисперсии dl |
случайных величин Al |
и Bl |
||
убывают достаточно быстро, так что ряд с положительными чле-
∞
нами ∑dl сходится. Эта сходимость обеспечивает абсолютную
l=1
сходимость ряда (3.13) и конечность дисперсии случайного процесса (3.12), так как
∞ |
|
Dξ = Kξ (0) = ∑dl . |
(3.14) |
l=1
Формула (3.13) дает разложение в ряд Фурье по косинусам четной 2T -периодической функции Kξ (τ) . Коэффициенты dl этого ряда
Фурье связаны с функцией Kξ (τ) формулой
|
|
1 |
T |
|
|
dl |
= |
|
∫Kξ(τ)cosωl τdτ (l =1,2,...) . |
(3.15) |
|
T |
|||||
|
|
−T |
|
||
|
|
|
|
Подынтегральная функция в правой части (3.15) четная, а промежуток интегрирования симметричен, поэтому
|
|
2 |
T |
|
|
dl |
= |
|
∫Kξ(τ)cosωl τdτ (l =1,2,...) . |
(3.16) |
|
T |
|||||
|
|
0 |
|
||
|
|
|
|
73
Если увеличивать T , уменьшая соответственно промежуток ∆ω = π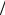
Т между частотами, то число слагаемых на любой фикси-
рованный интервал частот (ωa ,ωb ) в разложении (3.12) растет
обратно пропорционально ∆ω. Чтобы составляющая случайного процесса (3.12), приходящаяся на этот интервал частот, не возрастала бесконечно, должны выполняться условия
Al = AT (ωl )∆ω, Bl = BT (ωl )∆ω dl = ST (ωl )∆ω. |
(3.17) |
Перепишем формулы (3.12), (3.13) и (3.16) с учетом обозначений (3.17) и равенства (3.11):
∞ |
|
|
|
|
|
ξ(t) = mξ + ∑(AT (ωl )cosωlt + BT (ωl )sin ωlt)∆ω, |
(3.18) |
||||
l=1 |
|
|
|
|
|
∞ |
|
|
|
|
|
Kξ (τ) = ∑ST (ωl )cosωl τ∆ω, |
(3.19) |
||||
l=1 |
|
|
|
|
|
|
d |
2 |
|
|
|
ST (ωl ) = |
l |
= |
|
∫Kξ (τ)cosωl τdτ. |
(3.20) |
|
|||||
∆ω |
π |
||||
При стремлении ∆ω к нулю и соответственно T → ∞ спектр случайного процесса (3.18) из дискретного превращается в непрерывный, а представление его рядом переходит в интегральное представление:
∞ |
|
ξ(t) = mξ + ∫(A(ω)cosωt + B(ω)sin ωt)dω. |
(3.21) |
0 |
|
При этом формулы (3.19) и (3.20) принимают соответственно вид
∞ |
|
Kξ (τ) = ∫Sξ (ω)cosωτdω, |
(3.22) |
0 |
|
Sξ (ω) = 2 ∞∫Kξ(τ)cosωτdτ
π 0
(см. также формулу (2.14)).
Равенство (3.21) представляет стационарную функцию ξ(t) , аргументом которой является время
(3.23)
случайную t , через две
74
другие случайные функции A(ω) и B(ω) , аргументом которых является круговая частота ω. Исходя из свойств функций (3.17)
A |
(ω |
) = |
Al |
, |
B (ω |
) = |
Bl |
и S |
|
(ω ) = |
Dl |
. |
(3.24) |
|
|
||||||||||||
|
|
||||||||||||
∆ω |
|
||||||||||||
∆ω |
|
||||||||||||
T |
l |
|
|
T l |
|
|
T |
l |
∆ω |
|
|||
Отсюда можно получить представление о свойствах случайных функций A(ω) и B(ω) .
Функции AT (ωl ) и BT (ωl ) не коррелированы, и значения ка-
ждой из них при различных значениях аргумента не коррелированы, так что
M[AT (ωl )BT (ωl )] = 0,
M[AT (ωl )AT (ωk )] = M[BT (ωl )BT (ωk )] = 0 при ωl ≠ ωk .
Ввиду этого заключаем, что случайные функции A(ω) и B(ω)
не коррелированы и их значения при любых сколь угодно близких, но различных значениях аргумента ω не коррелированы.
Перейдем к рассмотрению дисперсий, помня, что константа выносится из-под знака дисперсии в квад-
рате: D[A |
(ω |
)] = D |
|
Al |
|
= |
D[Al ] |
= |
dl |
|
= |
ST (ωl ) |
, |
|
|
|
|
2 |
|
||||||||||
T |
l |
|
|
|
|
∆ω |
2 |
|
∆ω |
|
∆ω |
|
||
|
|
|
|
∆ω |
|
|
|
|
|
|
||||
D[Al ]= M [Al2 ] = dl . Аналогично находим
D[AT (ωl )] = D[BT (ωl )] = ST∆ω(ωl ) .
так как
(3.25)
Из |
(3.25) |
следует, что дисперсии случайных |
функций |
|||
|
A(ω) |
и |
B(ω) бесконечны. |
Из того, что |
ковариация |
|
|
K A |
(ωl ,ωk ) = M[AT (ωl )AT (ωk )] |
равна нулю при ωl ≠ ωk и равна |
|||
|
T |
|
|
|
|
|
|
ST (ωl ) |
при |
ωl = ωk , следует: |
|
|
|
|
∆ω |
|
|
|||
|
|
|
|
|
||
|
|
|
|
∞ |
|
|
|
|
|
|
∑K AT (ωl ,ωk )∆ω = ST (ωl ). |
(3.26) |
|
|
|
|
|
k=1 |
|
|
При ∆ω→ 0 формула (3.26) принимает вид |
|
|||||
|
|
|
|
∞ |
|
|
|
|
|
|
∫K A (ω1,ω2 )dω2 = Sξ (ω1) , |
(3.27) |
|
|
|
|
|
0 |
|
|
75
откуда заключаем, что
K A (ω1,ω2 ) = Sξ (ω1)δ(ω2 |
−ω1). |
(3.28) |
Аналогично для ковариационной функции KB (ω1,ω2 ) |
случайной |
|
функции B(ω) от частоты ω имеем равенство |
|
|
KB (ω1,ω2 ) = Sξ (ω1)δ(ω2 |
−ω1). |
(3.29) |
Таким образом, случайные функции |
A(ω) и B(ω) |
от частоты |
ω в спектральном разложении (3.21) стационарного случайного процесса с непрерывным спектром имеют ковариационные функции, пропорциональные δ-функции. Формула (3.23), полученная предельным переходом при ∆ω→ 0 из равенства (3.20), представ-
ляет спектральную плотность S (ω) |
дисперсии стационарного |
||
случайного процесса |
(3.21). Если в |
(3.22) |
положить τ = 0 и |
∞ |
|
|
|
Dξ = K(0) = ∫Sξ (ω)dω, |
то можно убедиться, |
что дисперсия про- |
|
0 |
|
|
|
цесса (3.21) равна площади под графиком его спектральной плот-
ности Sξ (ω) .
Если мы выделим аддитивную часть случайного процесса (3.21), соответствующую промежутку частот (ω1,ω2 ) в его спе к-
тре, то получим стационарный процесс
|
ω2 |
|
ξω1,ω2 |
(t) = ∫(A(ω)cosωt + B(ω)sin ωt)dω, |
(3.30) |
|
ω1 |
|
дисперсия которого определяется интегралом от спектральной плотности Sξ (ω) по промежутку [ω1,ω2 ] :
ω2 |
|
D[ξω1,ω2 (t)] = ∫Sξ (ω)dω. |
(3.31) |
ω1 |
|
Если весь интервал (0,∞) частот разбить на отдельные подынтер-
валы, то случайный процесс (3.21) будет представлен суммой некоррелированных слагаемых вида (3.30), а дисперсия этого процесса – суммой дисперсий этих слагаемых, вычисляемых по (3.31).
76