
- •Краткий курс лекций по геометрии и алгебре
- •Глава I кривые второго порядка
- •§ 1. Парабола
- •§ 2. Эллипс
- •§ 3. Гипербола
- •§ 4. Директрисы эллипса и гиперболы.
- •§ 5. Фокальный параметр эллипса и гиперболы
- •§ 6.Полярное уравнение эллипса, гиперболы, параболы
- •§ 7. Классификация кривых второго порядка (квп)
- •§8.Свойства определителей второго и третьего порядков
- •§ 9. Общая теория кривых второго порядка
- •§ 10. Инварианты кривой второго порядка
- •Глава II поверхности второго порядка
- •§ 11. Основная теорема о поверхностях второго порядка
- •§ 12. Цилиндрические поверхности
- •§ 13. Конические поверхности
- •§ 14. Поверхности вращения
- •§ 15. Эллипсоид
- •§16. Гиперболоид.
- •§ 17. Параболоид
- •Глава 1. Кривые второго порядка
- •Глава II. Поверхности второго порядка
- •Гомельский государствееный университет
§ 13. Конические поверхности
Определение 2.3.Конической поверхностьюназывается множе-
ство прямых (образующих), проходящих через некоторую точку (вершину) и пересекающих некоторую линию (направляющую)(рис.21).
45
Коническая ПВП— коническая поверхность с направляющей,
я вляющейся
КВП.
вляющейся
КВП.
Рис. 21. Рис. 22.
Выведем уравнение конической поверхности в случае, когда вершина совпадает с началом прямоугольной системы координат OXY, а направляющей служит эллипс:
![]()
Возьмем на поверхности конуса произвольную точку М1(х1,у1,z1)
(рис. 22}. Тогда параметрическое уравнение прямой OM1имеют вид:
х=х1t, y=y1t, z=z1t.
Прямая ОМ1пересекает направляющую в точке M(x,у,с), следова-
тельно, с=z1t, т.е.t=с/z1. Значит, х=х1t=(х1с)/z1, у=(су1)/z1.
Точка M принадлежит эллипсу, поэтому

![]() =1
=1
46
Умножим обе части последнего выражения на z12/c2, получаем
![]() (*)
(*)
Так как соотношению (*) удовлетворяет любая точка поверхнос-
ти, то
![]() (2.3)
(2.3)
— уравнение конической поверхности
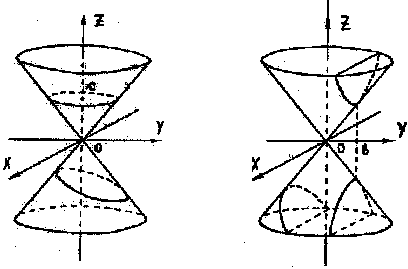
Рис. 23. Рис. 24.
В частности, если а=b, то получаем уравнение прямого круго-
вого конуса
х2+у2—k2z2=0, (**)
где k2=а2/с2.
Плоскость, параллельная плоскости ХОУ, пересекает конус (**)
по окружности. Например, плоскость z=1 пересекает конус (**) по окружности х2+y2=k2. Если немного наклонить эту плоскость, то в сечении получается эллипс (рис. 23).
47
Плоскости, параллельные плоскостям OYZ и OXZ, пересекают
конус по гиперболам (рис.24). Например, в сечении конуса (**)
плоскостью х=b, получаем кривую
b2+y2-k2z2=0,
т.е.![]()
Если секущая плоскость параллельна образующей конуса, то в
сечении получается парабола (рис. 24). Поэтому эллипс, гипербола и парабола называются коническими сечениями.
§ 14. Поверхности вращения
Определение 2.4.Поверхность называетсяповерхностью враще-
ния,если она вместе с каждой своей точкой содержит и всю окружность, полученную вращением этой точки вокруг некоторой фиксированной прямой, называемойосью вращении.
Пусть на плоскости YOZ задана кривая линия lуравнением вида
F(y,z)=0 (*)

(рис. 25). Найдем уравнение по-
верхности вращения, образован-
ной вращением кривой l вокруг
оси OZ. Возьмем произволь-
ную точку М1(x1,у1,z1) на полу-
ченной поверхности и проведем
через нее плоскость, перпенди
кулярную оси OZ. Обозначим точ
ки Р(0,0,z1) и М(0,у,z). Ради-
ус, полученной в сечении окруж-
ности равен: R=М1Р=РМ, т.е.
![]() Откуда
Откуда
48
![]() (**)
(**)
Так
как точка М принадлежит кривой l,
то, подставляя значение у из
(**) в уравнение (*),
получаем![]() .
Этому уравнению удовлетворяют
все точки поверхности, значит,
.
Этому уравнению удовлетворяют
все точки поверхности, значит,
![]() (2.4)
(2.4)
— искомое уравнение поверхности вращения.
Заметим, что знак в (2.4) выбирается таким образом, чтобы в
соответствующих точках, он совпадал со знаком ординаты у кривой l.
Аналогичным образом можно получить, что уравнение
![]()
задает поверхность вращения, образованную вращением кривой
F(x,z)=0 вокруг оси OZ.
