Гипербола

Определение. Гиперболой называется множество точек плоскости, абсолютная величина разности расстояний от каждой из которых до двух данных точек F₁ и F₂, называемых фокусами гиперболы, есть величина постоянная, равная 2а, а>0, меньшая чем расстояние между фокусами.

В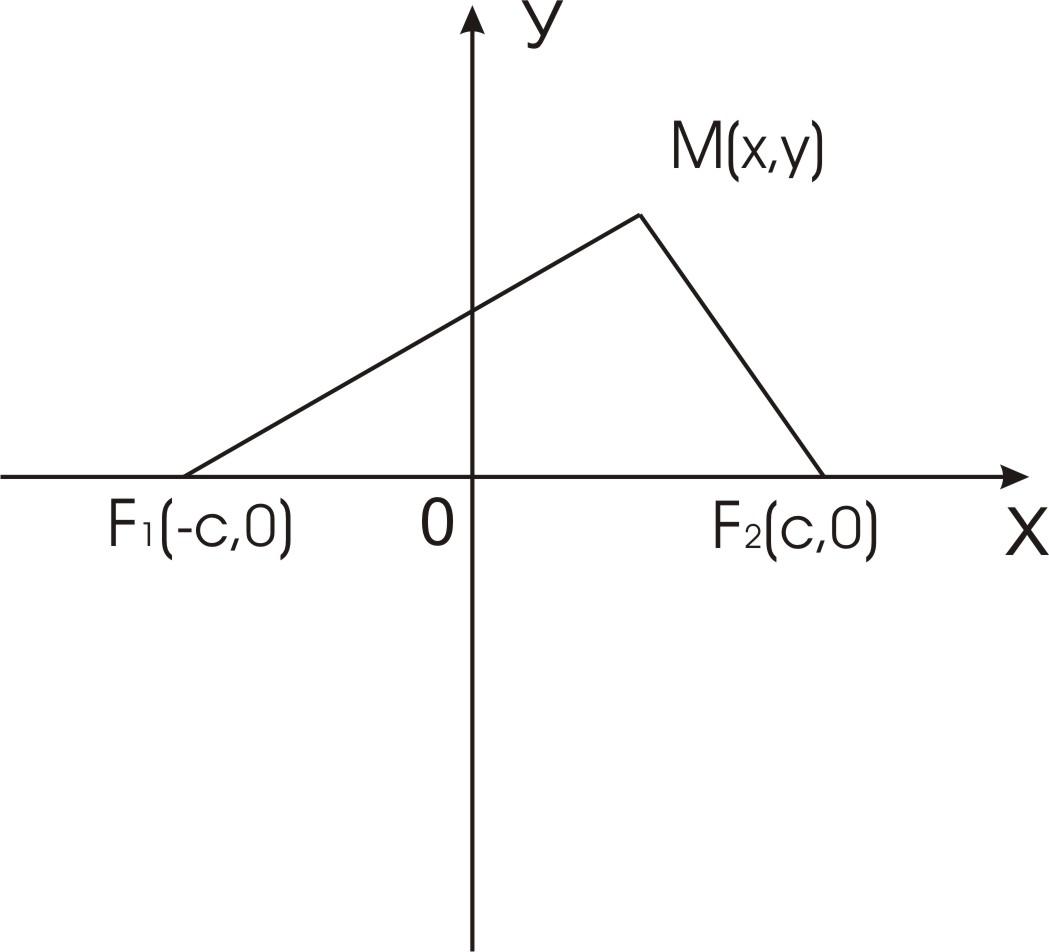ыберем декартову прямоугольную систему координат ОХY так, как показано на рисунке. Тогда F₁F₂=2с, F₁(—с,0), F₂(c,0). Для произвольной точки М(х,у), принадлежащей гиперболе, имеем МF₁—MF₂=2а, а<с.

Обозначим с²-а²=b², тогда каноническое уравнение гипрболы имеет вид:

. (3)

П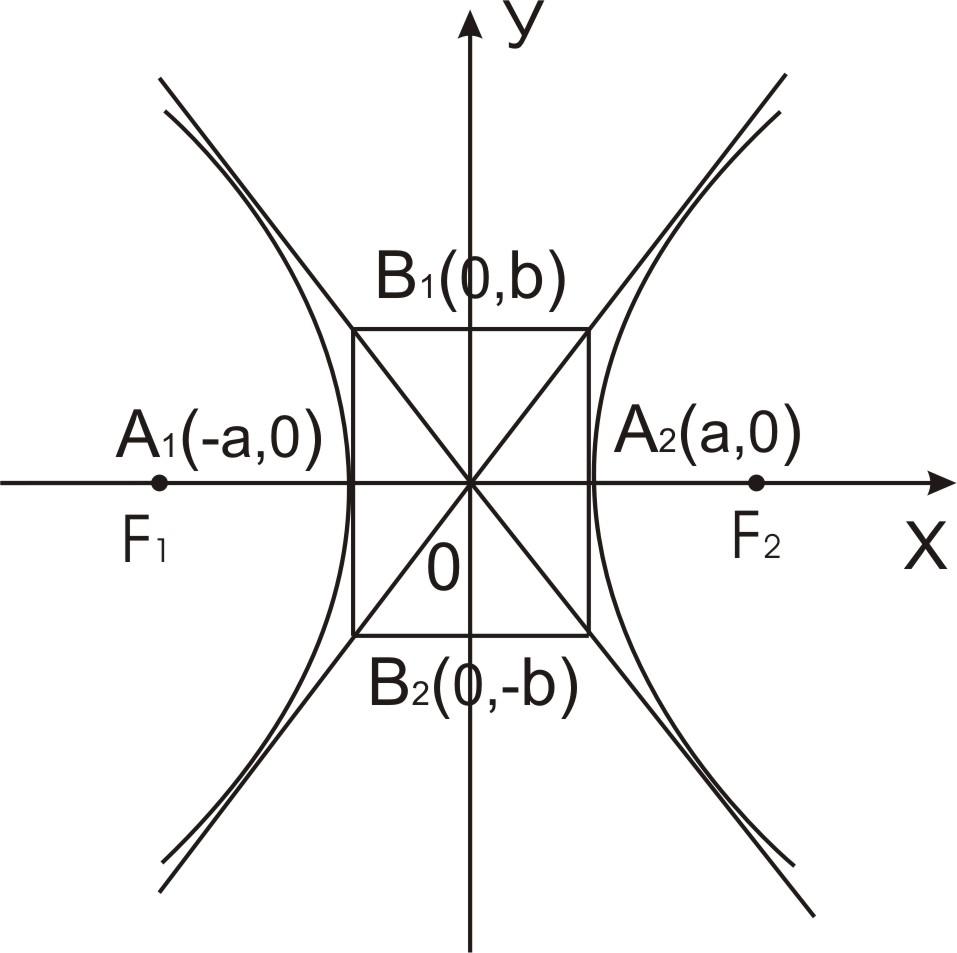о свойствам уравнения (3) исследуем свойства гиперболы:

1. Координатные оси являются осми симметрии гиперболы. Поэтому гиперболу достаточно исследовать только в первой координатной четверти.

2. Если у = 0, то x = а. Если х = 0, то уравнение (3)

решений не имеет. Значит, гипербола пересекает только ось ОХ в точках А₁(—а,0), А₂(а,0), называемых вершинами гиперболы.

3. Так как

|х|а. Поэтому гипербола расположена вне полосы, ограниченной прямыми x=а.

4. Если x возрастает от а до +, то из (1.12) следует, что у возрастает от 0 до + в первой координатной четверти.

5.

— наклонные асимптоты гиперболы.

По полученным свойствам строим гиперболу (рис.7). Отрезок А₁А₂ и его длина 2а называются действительной осью гиперболы, а отрезок ОА₁ и его длина а — действительной полуосью. Отрезок В₁В₂ и его длина 2b — мнимая ось гиперболы, а отрезок ОВ₁ и его длина b— мнимая полуось. Длина отрезка F₁F₂=2с называется фокусным расстоянием, начало координат — центр гиперболы.

x²—у²=а²

Определение. Эксцентриситетом гиперболы называется величина

.

Так как для гиперболы с>а, и следовательно, чем меньше ε, тем более сжата гипербола к оси ОХ.

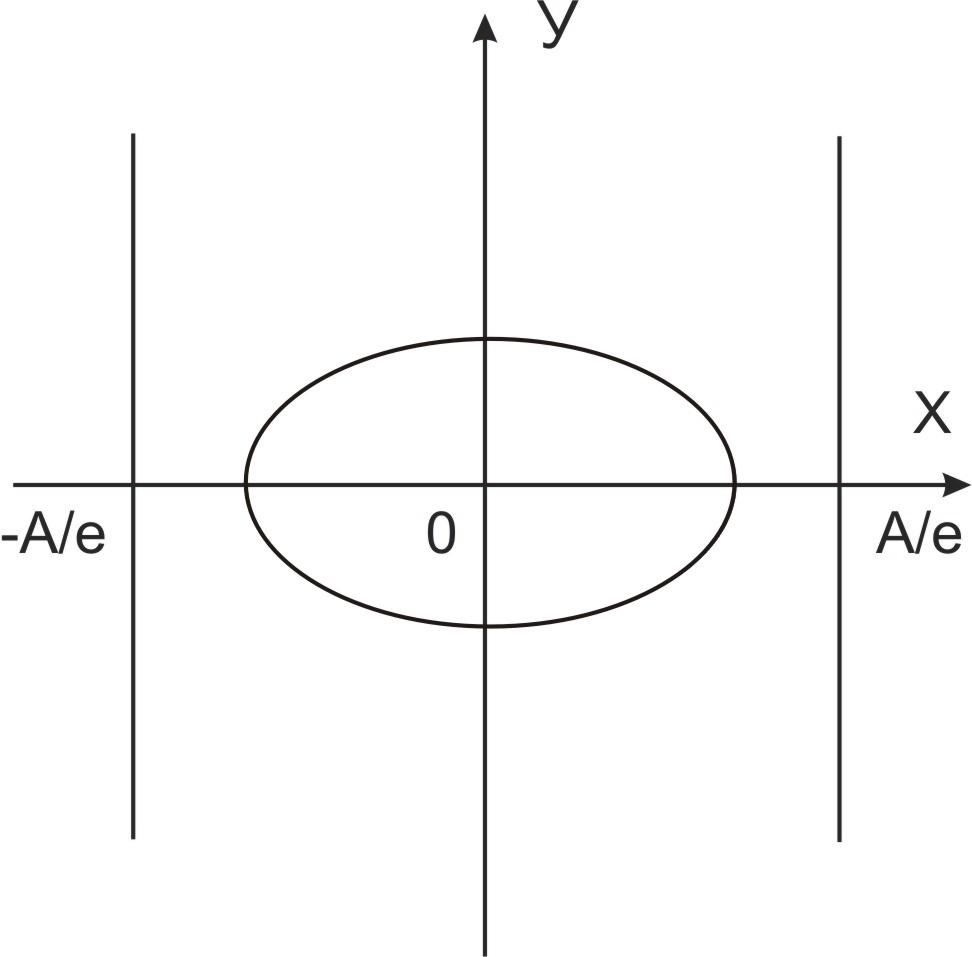
Директрисы эллипса и гиперболы.

Определение. Прямые х=(а/ε), где ε — эксцентриситет эллипса (гиперболы) называются директрисами эллипса (гиперболы).

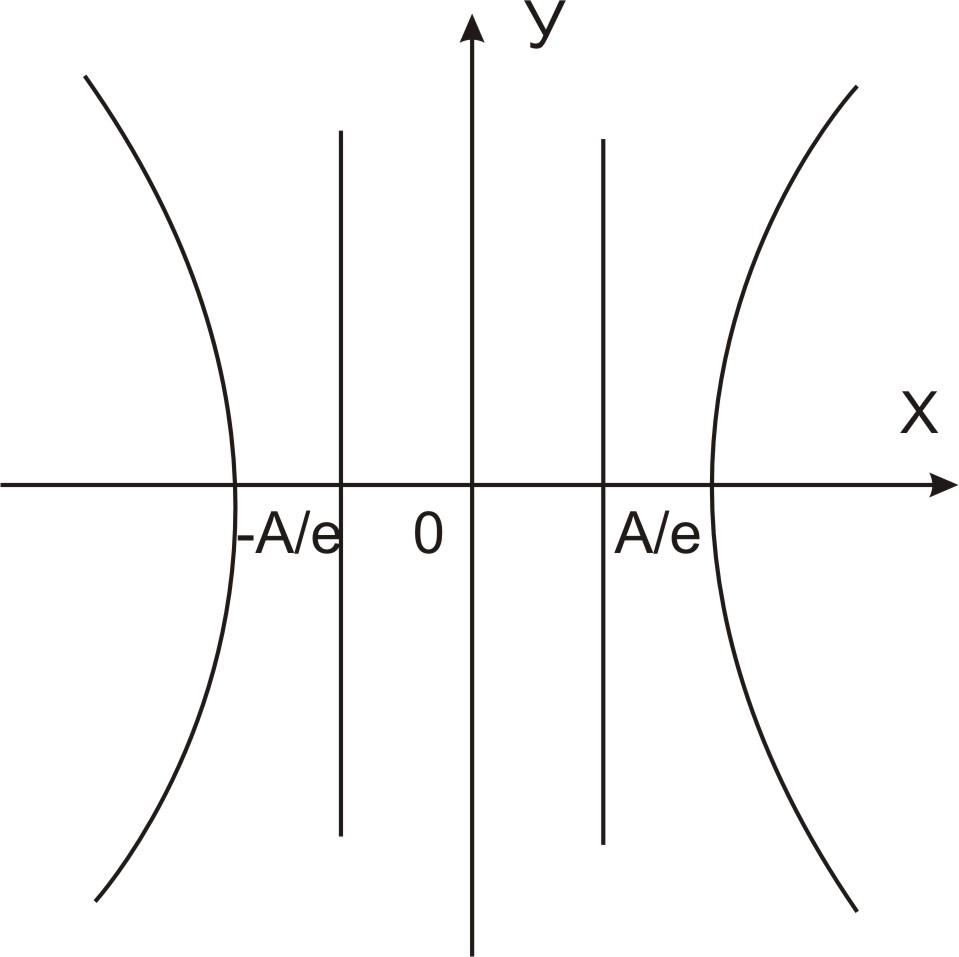
Теорема. Отношение расстояния от любой точки эллипса (гиперболы) до фокуса к расстоянию до соответствующей директрисы есть величина постоянная, равная эксцентриситету эллипса (гиперболы).

Доказательство, например для эллипса, следует из того, что

MF₁=а+εх, МF₂=а—εх.

З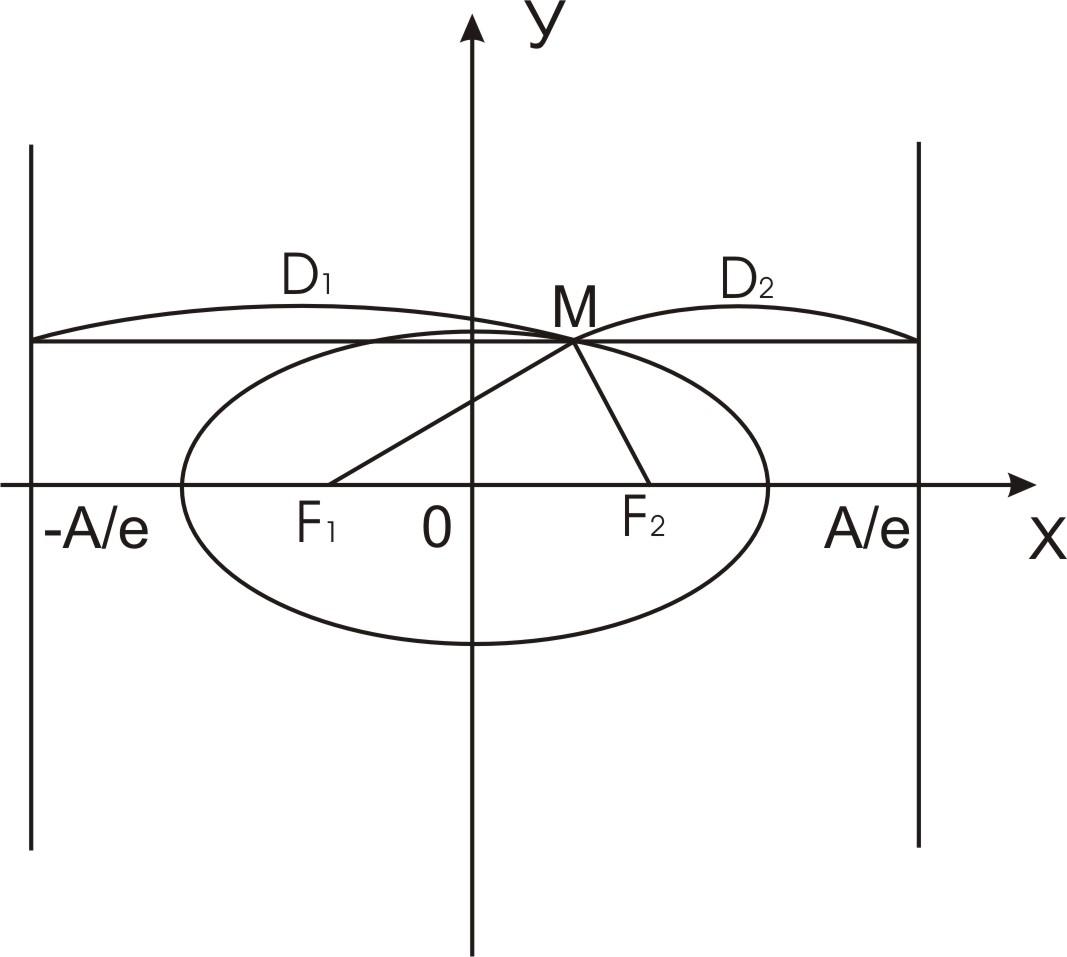аметим, что, так как все точки параболы равноудалены от директрисы и фокуса, то отношение этих расстояний равно 1. Пo этому можно говорить об эксцентриситете параболы и считать его равным 1. Как уже отмечалось, эксцентриситет окружности равен нулю.

Фокальный параметр эллипса и гиперболы

Пусть эллипс и гипербола заданы соответственно своими каноническими уравнениями. Проведем через один из фокусов этих кривых прямую перпендикулярную оси ОХ и обозначим точки ее пересечения с кривой через Р и Р'.

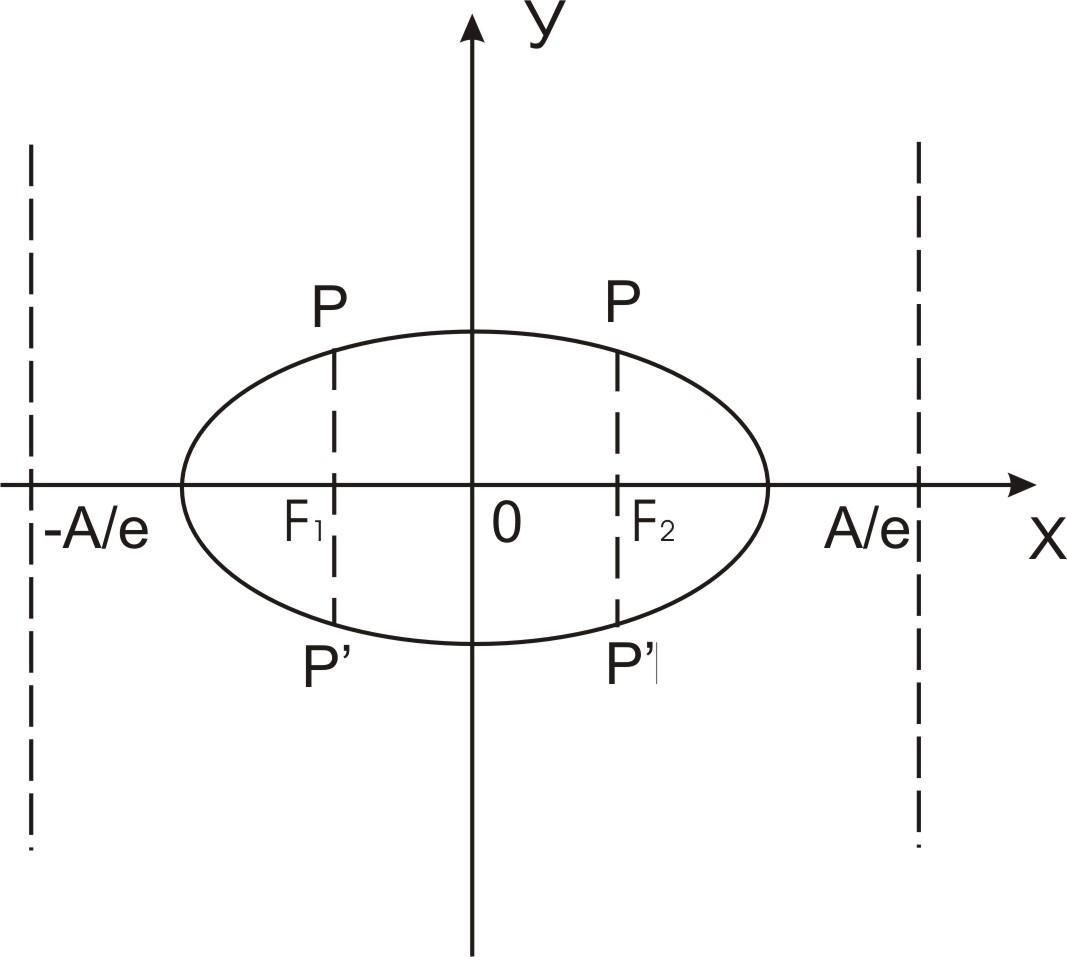
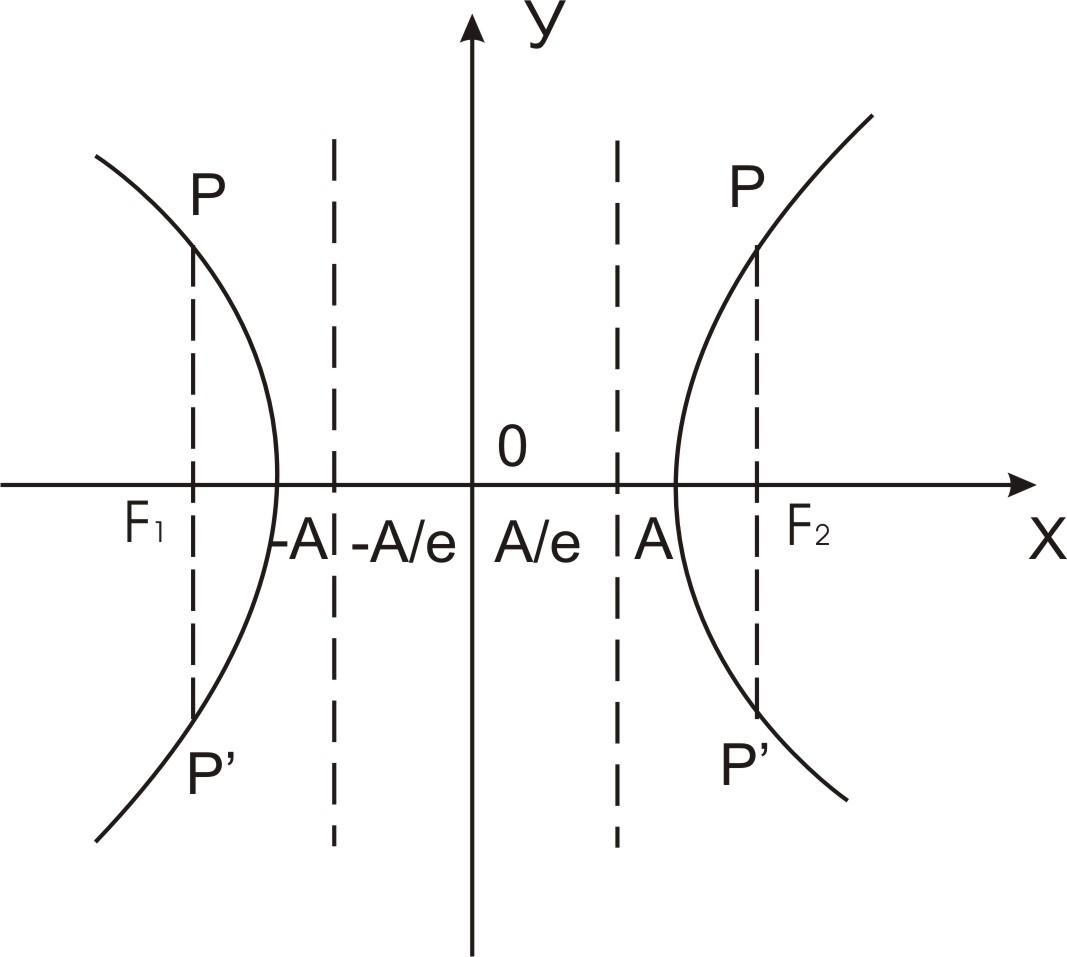
Обозначим длину отрезка РР' через 2р. Тогда величина р(р>0) называется фокальным параметром эллипса (гиперболы) и равна: .

Если обозначить через d – расстояние между фокусом и деректрисой, то .

Так как для параболы ε = 1 и d = р, то делаем следующий Вывод: для эллипса (кроме окружности), гиперболы, парабол фокальный параметр р равен:

p=εd,

где c — эксцентриситет, d — расстояние от фокуса до соответствующей директрисы.

Заметим, что для окружности фокальный параметр равен ее радиусу.