Проекции.

Назовем осью прямую, на которой указано направление, которое будем называть положительным.

Пусть l - некоторая ось, α - плоскость, непараллельная оси l. Через произвольную точку А пространства проведем плоскость α'||α и обозначим точку пересечения плоскости α' c осью l через А₁. Тогда точка А₁ называется проекцией точки А на ось l относительно плоскости α. В частности, если αl, то проекция называется прямоугольной, или ортогональной.

Пусть теперь задан вектор . Возьмем проекции А₁ и В₁ точек А и В на ось l относительно плоскости α.

Тогда вектор называется проекцией вектора на ось l относительно плоскости α. Величиной проекции вектора на осьl относительно плоскости α называется число, равное:

а) ||, если направление вектора совпадает с направлением оси l;

б) - ||, если направление противоположно направлено оси l.

Обычно из контекста ясно о проекции относительно какой плоскости идет речь. Поэтому величину проекции вектора на осьl будем обозначать Пр_l, а для ортогональной проекции использовать обозначение пр_l.

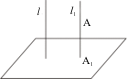Пусть α - некоторая плоскость и l – прямая, такая, что l не параллельна α. Через произвольную точку А пространства проведем прямую l₁ || l и обозначим точку пересечения прямой l₁ с плоскостью α через А₁. Точка А₁ называется проекцией точки А на плоскость α относительно прямой l.

Если прямая lα, то проекция называется прямоугольной, или ортогональной.

Определение. Углом между двумя векторами, или между осями, или между вектором и осью называется наименьший угол α, на который надо повернуть один из векторов или одну из осей до совпадения по направлению с другим вектором или осью.

Из определения следует, что 0απ. Угол между векторами или между осями, или между вектором и осью будем обозначать соответственно: (), (), ().

Теорема. Проекция вектора на ось обладает следуицики свойствами:

1) ;

2)

3) .

Скалярное произведение векторов.

Определение. Скалярным произведением векторов иназывается число (которое обозначается), равное произведению длин этих векторов на косинус угла между ними, т.е.

.

Из первого пункта предыдущей теоремы сразу следует, что

.

Так как соs 0 = 1. то =||². Следовательно,

,

где выражение =² называется скалярным квадратом вектора .

Теорема. Скалярное произведение двух векторов обладает следующими свойствами:

1) =(коммутативность);

2) λ () = (λ),λR;

3)(+) =+(дистрибутивность).

Из определения следует, что

.

Tеорема (необходимое и достаточное условие ортогональности двух векторов). Два ненулевых вектора взаимно перпендикулярны (ортогональны) тогда и только тогда, когда их скалярное произведение равно нулю.

Векторное произведение двух векторов.

Определение. Упорядоченная тройка некомпланарных векторов ,,называетсяправой, если при приведении их к общему началу поворот от вектора к векторупо кратчайшему пути виден с конца векторапротив часовой стрелки. Если же такой поворот осуществляется по часовой стрелке, то вектора,,образуютлевую тройку векторов.

1) 2)

Определение. Векторным произведением двух векторов иназывается вектор, обозначаемыйи удовлетворяющий следующим условиям:

1) ||=||||sin (^,);

2) ,;

3) векторы ,,образуют правую тройку векторов.