ГОМЕЛЬСКИЙ ГОСУДАРСТВЕЕНЫЙ УНИВЕРСИТЕТ

ИМЕНИ Ф.СКОРИНЫ

Кафедра алгебры и геометрии

А.Д.Ходалевич

Основное содержание лекционного курса

«Геометрия и алгебра»

для специальности «Прикладная математика».

Часть I. Аналитическая геометрия.

ГОМЕЛЬ 2004

Аналитическая геометрия - это раздел математики, в котором геометрические объекты изучаются с помощью алгебраических мето­дов, в основе которых лежит понятие координат.

ГЛАВА 1. ВЕКТОРЫ И КООРДИНАТЫ

§ 1. Понятие вектора

Пусть А – произвольное непустое множество. Декартовым квадратом А называется множество

A² =

Бинарным отношением на А называется любое подмножество множестваA².

Отношением эквивалентности на А называется такое бинарное отношение на А, которое удовлетворяет следующим условиям:

1) (рефлексивность);

2) если (,b)то (b,)(симметричность);

3) если (,b) то (,c)(транзитивность).

Теорема. Любое отношение эквивалентности на множестве А определяет разбиение этого множества на попарно непересекающиеся классы (классы эквивалентности). Обратно, любое разбиение множества А на попарно непересекающиеся классы определяет отношение эквивалентности на А.

Направленный отрезок – отрезок, у которого указано, какая точка является началом, а какая концом. Обозначается .

Пусть заданы направленные отрезки и, лежащие на двух различных параллельных прямых, и плоскость, проходящая через точки В иD. Тогда плоскостьразбивает все пространство на два полупространства. Если при этом точкиB и D лежат в одном полупространстве, то говорят, что направленные отрезки иодинаково направлены (обозначается ). В противном случае, они называютсяпротивоположно направленными (обозначается ).

Если направленные отрезки илежат на одной прямой, то они одинаково (противоположно) направленны, если существует такой третий направленный отрезок, который одинаково направлен с каждым из направленных отрезкови(противоположно направлен в точности с одним из направленных отрезковили).

Абсолютной величиной или модулем (длиной) направленного отрезка называется длина этого направленного отрезка и обозначается ||.

Два направленных отрезка иназываютсяравными, если и, при этом пишут=,

Теорема. Отношение равенства направленных отрезков является отношением эквивалентности.

Тогда вектором называется абстрактный объект, совпадающий с некоторым классом эквивалентности.

Таким образом, каждый из равных друг другу направленных отрезков считается представлением (изображением) данного вектора, а неравные направленные отрезки считаются представлением разных векторов. Поэтому в дальнейшем вектор изображается точно так, как и соответствующий ему направленный отрезок.

Векторы иназываютсяколлинеарными, если образующие их направленные отрезки параллельны одной и той же прямой (обозначается ||).

Три и более векторов называются компланарными, если образующие их направленные отрезки параллельны некоторой плоскости.

Нулевым вектором называется вектор, начало которого совпадает с его концом (обозначается ). Направление нулевого вектора не определено.

Линейные операции над векторами.

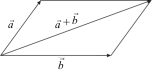
Определение. Суммой + векторов и называется вектор, проведенный из начала к концу , если конец и начало совпадают. Приведенное определение сложения векторов называется правилом треугольника. Векторы и можно складывать, пользуясь правилом параллелограмма.

Если имеется n векторов , то их сумма определяется как вектор.

Определение. Разностью векторов и называется такой вектор =-, что выполняется равенство +=.

Легко показать, что для любого вектора , существует такой единственный вектор , называемый противоположным вектору

что +=. Вектор, противоположный вектору , будем обозначать –.

Определение. Произведением вектора на число λ (λ0) называется вектор =λ, удовлетворяющий следующим условиям:

1) векторы и одинаково направлены, если λ>0, и противоположно направлены, если λ<0;

2) ||=|λ|||.

По определению, произведение произвольного вектора на число 0 есть нулевой вектор, т.е. 0=.

Введенные операции сложения векторов и умножение вектора на число называются линейными. Они обладают следующими свойствами:

1) сложение векторов коммутативно:

+=+, ,;

2) сложение векторов ассоциативно:

(+)+=+(+),  ,,;

3) +=, ;

4) +(-)=0, ;

5) умножение вектора на число ассоциативно:

α (β ) = (α β),  α, β  R;

6) 1=, ;

7) умножение вектора на число дистрибутивно по отношению к

сложению чисел:

(α+β)=α+β, , α, β  R;

8) умножение вектора на число дистрибутивно по отношению к сложению векторов:

α(+)=α+α,  ,,  α  R;

Множество всех векторов пространства (плоскости), удовлетворяющих свойствам 1) – 8), называется линейным, или векторным пространством, и обозначается ().

Теорема (необходимое и достатаочное условие коллинеарности двух векторов). Для того чтобы векторы и были коллинеарны, необходимо и достаточно, чтобы существовало λ, удовлетворяющее условию:

= λ.