
- •Линейная и векторная алгебра
- •Общие методические указания
- •Операции над матрицами.
- •Определители матриц второго и третьего порядка.
- •Системы линейных алгебраических уравнений
- •Построение общего решения методом Гаусса:
- •Задание 1
- •Задание 2
- •Задание 3.
- •Векторная алгебра и аналитическая геометрия.
- •4 Прямая на плоскости
- •Плоскость.
- •Прямая и плоскость в пространстве.
- •Задание 4.
- •Задание 7.
- •Задание 8
- •Кривые второго порядка
- •Окружность
- •Гипербола
- •Парабола
Задание 1
Для определителя
 найти алгебраические дополнения
элементов аi,2;
a3j
найти алгебраические дополнения
элементов аi,2;
a3j
Вычислить определитель:
А) разложив по элементам i- той строки;
Б) разложив по элементам j- того столбца;
В) получив предварительно два нуля в i- той строке
1
 .
2.
.
2. 3
3 .
.
4.
 5
5 .
6.
.
6.
7.
 8.
8.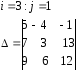 9.
9.
10.
 11.
11. 12.
12.
13. 14.
14. 15.
15.
16. 17.
17.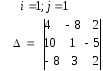 18
18
19. 20.
20. 21.
21.
22.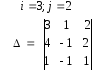 23.
23. 24.
24.
25. 26.
26. 27.
27.
28. 29.
29. 30.
30.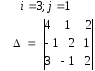
Задание 2
Даны две матрицы А и В. Найти:
а) А*В и В*А;
б) обратную матрицу А-1;
Доказать:
А-1*А
= А* А-1
= Е =

1. ;
;
 ;
;
3.
4.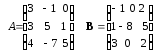
5.
6.
7.
8.
9.

10.
11.
12.
13.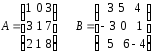
14.
15.
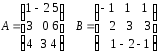
16.
17.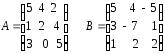
18.
19.
20.

21.
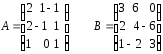
22.
23.
24.
25.

26.
27.
28.
29.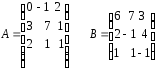
30.
Задание 3.
Проверить на совместимость и решить систему линейных алгебраических уравнений:
а) по формулам Крамера;
б) с помощью обратной матрицы;
в) методом Гаусса;
1.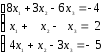 2.
2.
3.
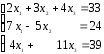 4.
4.
5.
 6.
6.
7.
 8.
8.
9.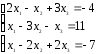 10.
10.
11. 12.
12.
13.
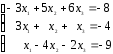 14.
14.
15. 16.
16.
17. 18.
18.
19. 20.
20.
21. 22.
22.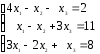
23. 24.
24.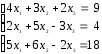
25. 26.
26.
27. 28,
28, .
.
29 , 30,
30,
Векторная алгебра и аналитическая геометрия.
Определение 2.1. Геометрическим вектором или просто вектором называется направленный отрезок.
Определение
2.2.
Суммой двух векторов
![]() и
и ![]() называется третий вектор
называется третий вектор
![]() +
+![]() ,
который идёт из начала первого вектора
,
который идёт из начала первого вектора![]() в конец второго
в конец второго![]() ,
если второй вектор выходит из конца
первого. (рис. 1)
,
если второй вектор выходит из конца
первого. (рис. 1)
Определение
2.3.
Разностью двух векторов
![]() и
и![]() называется третий вектор
называется третий вектор![]() -
-![]() ,
который представляет собой сумму вектора
,
который представляет собой сумму вектора![]() и вектора противоположного вектору
и вектора противоположного вектору![]() ,
т.е.
,
т.е.![]() -
-![]() =
=![]() +(-
+(-![]() ).
).
Определение
2.4.
Произведением вектора
![]() на числоx
называется вектор, обозначаемый
на числоx
называется вектор, обозначаемый
![]()
![]() ,
такой, что: 1) |
,
такой, что: 1) |![]()
![]() |=|
|=|![]() |∙|
|∙|![]() |
|
2)
векторы
![]() и
и![]()
![]()
имеют
одно направление, если
![]() >0,
и противоположное, если
>0,
и противоположное, если![]() <0.
<0.
Определение
2.5.
Если вектор
![]() составляет с осьюОх
угол
составляет с осьюОх
угол
 ,
то проекцией вектора на эту ось называется
произведение модуля вектора на косинус
угла
,
то проекцией вектора на эту ось называется
произведение модуля вектора на косинус
угла
 :
:

Проекция
суммы векторов
![]() и
и
![]() на осьОх
равна сумме проекций этих векторов на
эту ось:
на осьОх
равна сумме проекций этих векторов на
эту ось:

В
трёхмерном пространстве
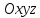 вектор
вектор
![]() может быть представлен разложением по
координатному базису в виде:
может быть представлен разложением по
координатному базису в виде: ,
где
,
где ,
,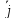 ,
, -
единичные базисные векторы, направление
каждого из которых совпадает с
положительным направлением соответствующей
оси;
-
единичные базисные векторы, направление
каждого из которых совпадает с
положительным направлением соответствующей
оси;
 ,
, ,
,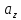 -
проекции вектора
-
проекции вектора![]() на оси координат.
на оси координат.
Определение
2.6.
Длина (модуль) вектора определяется
через проекции по формуле

Направление вектора определяется его направляющими косинусами:

Направляющие косинусы вектора связаны соотношением:
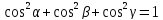
Пример № 1
Найти
длину вектора
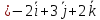
Решение:

Пример № 2
Даны
векторы
 и
и .
Найти сумму векторов
.
Найти сумму векторов![]() и
и
![]() .
.
Решение:
Если
векторы
![]() и
и![]() заданы их разложением по ортам, то их
сумма и разность определяются по
формулам:
заданы их разложением по ортам, то их
сумма и разность определяются по
формулам:

В
нашем случае:
 ,
т.е.
,
т.е.
Пример № 3
Указать
значение направляющих косинусов вектора

Решение:
Направление
вектора
![]() определяется углами
определяется углами образованными
им с осями координат
образованными
им с осями координат



Пример № 4
Разложить
вектор
 по векторам
по векторам
 и
и
Решение:
Требуется
представить вектор
 в виде
в виде ,
где
,
где -
числа. Найдём их, используя определение
равенства векторов. Имеем:
-
числа. Найдём их, используя определение
равенства векторов. Имеем: ,
,
 ,
, и равенство
и равенство ,
т.е.
,
т.е.
 . Отсюда
следует:
. Отсюда
следует:
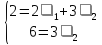
Решая
систему уравнений, находим:
 ;
;
 ,
следовательно,
,
следовательно, .
.
Определение 2.7. Скалярным произведением векторов называется произведение их модулей на косинус угла между векторами:

Если
векторы выражены через координаты в
декартовой системе координат
 ,
, ,
то скалярное произведение определяется
как сумма попарных произведений
соответствующих координат:
,
то скалярное произведение определяется
как сумма попарных произведений
соответствующих координат:

Условием
перпендикулярности векторов
![]() и
и![]() является равенство нулю их скалярного
произведения:
является равенство нулю их скалярного
произведения: или
или .
.
Скалярное произведение обладает следующими свойствами:

 .
.
Модуль
вектора
![]() может быть представлен в виде
может быть представлен в виде ,
где
,
где -
скалярный квадрат вектора
-
скалярный квадрат вектора![]() ,
равный
,
равный .
.
Пример № 5
Определить
угол между векторами:
 и
и
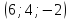
Решение:
Согласно
определению скалярного произведения
двух векторов
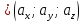 и
и ;
;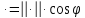
Следовательно,

В
нашем случае,


Пример № 6
Вычислить:
 .
.
Решение:
Скалярное
произведение ортов осей координат
равно:
 ,
,
 ,
следовательно,
,
следовательно,

Определение 2.8.
Векторным произведением двух векторов называется третий вектор, длина которого численно равна площади параллелограмма, построенного на данных двух. Этот вектор перпендикулярен к плоскости параллелограмма и направлен так, что если смотреть с его конца в основание, то кратчайший поворот от первого ко второму веден происходящим против хода часовой стрелки.

Если
векторы заданы своими координатами
 ,
,
 ,
то векторное произведение можно найти
через определитель:
,
то векторное произведение можно найти
через определитель:

Пример № 7
Найти
площадь треугольника с вершинами
 ,
, и
и .
.
Решение:
Площадь
 треугольника
треугольника равна половине площади параллелограмма,
построенного на векторах
равна половине площади параллелограмма,
построенного на векторах и
и ,
т.е.
,
т.е. .
.
Имеем


Найдём векторное произведение этих векторов:
 ,
,
Следовательно,
 .
.
Определение 2.9.
Смешанным
произведением упорядоченной тройки
векторов
 называется скалярное произведение
первого вектора на векторное произведение
второго вектора на третий и обозначается
называется скалярное произведение
первого вектора на векторное произведение
второго вектора на третий и обозначается .
.
Если
векторы заданы своими координатами
 ,
,
 ,
,
 их смешанное
произведение можно записать через
определитель
их смешанное
произведение можно записать через
определитель

Модуль
смешанного произведения трех векторов
 ,
,
 и
и равен объёму параллелепипеда, построенного
на этих векторах, как на сторонах.
равен объёму параллелепипеда, построенного
на этих векторах, как на сторонах.
Если
известны вершины
 ,
, и
и ,
, треугольной пирамиды, то ейё объём можно
вычислить по формуле
треугольной пирамиды, то ейё объём можно
вычислить по формуле .
.
Пример №8
Найти
объём треугольной пирамиды, построенной
на векторах
 ,
,
 ,
, .
.
Решение:
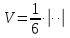
Найдём смешанное произведение данных векторов:

Следовательно,
 (куб. ед.)
(куб. ед.)
Пример №9
При
каком значении
![]() векторы
векторы ,
,
 ,
,
 компланарны?
компланарны?
Решение:
Условием
компланарности трех векторов является
условие равенства нулю смешанного
произведения этих векторов, т.к.
 .
.
Составим
и решим уравнение:
 .
.
Вычислим определитель в левой части равенства:
 ,
следовательно,
,
следовательно,
 .
.
Определение 2.10.
Полярными
координатами точки
 называются
радиус-вектор ρ - расстояние от точки
называются
радиус-вектор ρ - расстояние от точки
 до заданной точки
до заданной точки (полюса) и полярный угол φ - угол между
прямой
(полюса) и полярный угол φ - угол между
прямой и заданной прямой, проходящей через
полюс. Полярный угол считается
положительным при отсчете от полярной
оси против часовой стрелки и отрицательным
при отсчете в обратную сторону.
Координатные линии в полярных системах
- окружности с центром в полюсе и лучи.
и заданной прямой, проходящей через
полюс. Полярный угол считается
положительным при отсчете от полярной
оси против часовой стрелки и отрицательным
при отсчете в обратную сторону.
Координатные линии в полярных системах
- окружности с центром в полюсе и лучи.
Формулы для перехода от полярных координат к декартовым:
 и обратно,
и обратно,
 ,
,
Определяя
величину
 ,
следует определить четверть, в которой
лежит точка
,
следует определить четверть, в которой
лежит точка
 и учитывать, что
и учитывать, что .
.
Пример № 10
Найти
полярные координаты точки
 .
В нашем случае имеем
.
В нашем случае имеем ,
,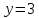 ,
, ,
, .
.
Точка
 лежит в первой четверти, следовательно,
лежит в первой четверти, следовательно, .
Итак,
.
Итак, .
.
Пример № 11
Определить
расстояние между точками
 и
и .
.
Решение:
Расстояние между двумя точками с полярными координатами можно найти двумя способами.
I
способ:
Переведём точки
 и
и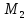 в прямоугольные координаты.
в прямоугольные координаты.
Точка
 ,
, ,
следовательно,
,
следовательно,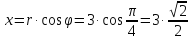 ;
;
 ,
тогда в ДСК точка
,
тогда в ДСК точка
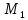 имеет координаты
имеет координаты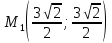 ,
,
Соответственно,
 .
.
Тогда
расстояние

II
способ:
 ,
подставляя значения
,
подставляя значения ,
, ,
, ,
, ,
,
Имеем
 .
.
Задания:
Найти длину вектора
 и его направляющие косинусы.
и его направляющие косинусы.Векторы
 и
и образуют угол
образуют угол ,
причем
,
причем .
Определить
.
Определить
Определить, при каких значениях
 и
и векторы
векторы коллинеарны.
коллинеарны.На плоскости даны три вектора
 .
Разложить вектор
.
Разложить вектор по
векторам
по
векторам
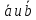 .
.Найти проекцию вектора

