Определители матриц второго и третьего порядка.

Определение 1.5. Определителем матрицы второго порядка называется число

Определение 1.6. Определителем матрицы третьего порядка называется число

Пример №7

Вычислить определители и в ответе указать произведение их значений:

Решение:

Удобнее всего вычислять определитель разложением по строке или столбцу, содержащим наибольшее количество нулей. В данном примере определитель третьего порядка преобразуем, используя свойство определителя:

==

Разложим определитель по третьей строке.

Пример №8. При каком значении х

Решение:

Для решения уравнения, вычислим определитель, разложив его по строке, содержащей неизвестную переменную:

Следовательно:

Пример №9. Решить уравнение:

Решение:

следовательно

Задания:

1.Вычислить определители: а) 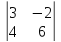, б) , в)

2.Решить уравнения и неравенства: а) , б) , в)

Системы линейных алгебраических уравнений

Система линейных алгебраических уравненийснеизвестными - это система уравнений вида

Здесь — количество уравнений, а— количество неизвестных.

— неизвестные, которые надо определить.

— коэффициенты системы,— свободные члены.

Решение системы — совокупность чисел, таких, что подстановка каждоговместов систему обращает все её уравнения втождества.

Система уравнений называется совместной, если она имеет хотя бы одно решение.

Теорема Кронекера –Капелли:

Система линейных алгебраических уравненийсовместнатогда и только тогда, когдаранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Общее решение системы уравнений можно получить с помощью формул Крамера или методом Гаусса.

Формулы Крамера:

Система линейных уравнений, в которой число уравнений равно числу неизвестных и определитель матрицы системы не равен нулю, имеет единственное решение, которое определяется по формулам: , где- определитель матрицы системы;- определитель, получаемый из определителязаменой-го столбца столбцом свободных членов.

Построение общего решения методом Гаусса:

1. Проверить, имеется ли в системе противоречивое уравнение. Если такое уравнение в системе есть, то она несовместна и не имеет общего решения.

2. Вычеркнуть все тривиальные уравнения в системе, если они есть.

3. Выяснить, является ли система уравнений разрешенной. Если она разрешенная, то построить общее решение, выражая разрешенные неизвестные через свободные.

4. Найти уравнение в системе, не содержащее разрешенного неизвестного. С помощью элементарных преобразований получить в этом уравнении неизвестное с коэффициентом единица, а затем исключить это неизвестное из остальных уравнений системы.

5. Перейти к выполнению пункта 1. Через конечное число шагов процесс остановится и будет установлена несовместность системы или получено общее решение системы линейных уравнений.

Пример №10. Решить систему и в ответе указать произведение решений:

Решение:

Решим систему уравнений по формулам Крамера. Для этого найдем определитель матрицы системы:

так как , то решение системы существует и единственно. Найдем определители D_1, D_2, D₃ подставляя столбец свободных членовнашего первого, второго и третьего столбцов определителяD соответственно.

Отсюда получаем решение системы уравнений:

;;

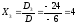
Подстановкой корней в систему уравнений, убеждаемся, что , являются решением системы. Следовательно,- произведение решений.

Пример №11. При каком значении система совместна и неопределенна:

Решение:

Приведем к ступенчатому виду расширенную матрицу системы:

При 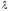=6, получаем расширенную матрицу системы

, её ранг равен 1, значит. Ранг матрицы меньше количества неизвестных т. е. меньше, значит система совместна и неопределенна

Пример №12. Указать общее решение однородной системы

Решение:

Запишем матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований:

Так как , то система неопределенна. Количество главных переменных равноr(A)=1: количество сводных переменных равно

Пусть главной переменной будет х₁, тогда из равенства 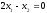, следует, что. Обозначим черезt главную переменную, тогда общее решение системы:

Пример №13. Указать фундаментальную систему уравнений:

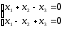
Решение:

Запишем матрицу системы и приведем ее к ступенчатому виду с помощью элементарных преобразований.

Так как (n – количество переменных), то система определена. Количество главных переменных равно , количество свободных переменных равно.

Для определения главных переменных выберем какой-нибудь неравный нулю минор второго порядка полученной матрицы А, например, минор .Его столбцы соответствуют переменным х₁ и х₂ – это будут главные переменные а х₃ – свободная переменная. Запишем систему, соответствующую полученной матрице:

из второго уравнения выражая х₂ через х_3, получим х₂ = х₃; подставляя это выражение в первое уравнение, получим =0.Обозначим свободную переменную черезt получим общее решение системы: (0;t;t) = t(0;1;1). Фундаментальную систему решений образует, например, решение

Задания:

1. Найти решения систем уравнений:

а) б)

2. Найти общее решение системы линейных уравнений методом Гаусса:

а), б)

Индивидуальные задания