Задача к.4

На рисунках К.4.0 – К.4.9 схематично показано механізми, у яких деяка частина тіл (деталі або їх частини) може бути представлена в якості матеріальних точок, що здійснюють складний рух.

Умова задачі. Прямокутна пластина (рис. К.4.0 - К.4.4) або кругла пластина радіуса R = 60 см (рис. К.4.5 – К.4.9) обертається навколо нерухомої осі за законом, який задано в таблиці 10. Умови задач К.4.0 – К.4.9, у таблиці 11. Умови задач К.4.0.А – К.4.9.А або в таблиці 12. Умови задач К.4.0.Б – К.4.9.Б залежно від рівня складності задачі. У задачі першого рівня складності (таблиця 10. Умови задач К.4.0 – К.4.9) задана кутова швидкість обертання пластини . У задачах другого та третього рівнів складності (таблиця 11. Умови задач К.4.0.А – К.4.9.А, таблиця 12. Умови задач К.4.0.Б – К.4.9.Б) задано закон обертання пластини . Додатний напрямок відліку кута повороту (відповідно кутової швидкості ) показано на рисунках дуговою стрілкою. Якщо задана кутова швидкість <0, то дугову стрілку на рисунку необхідно показати в напрямку, протилежному до напрямку .

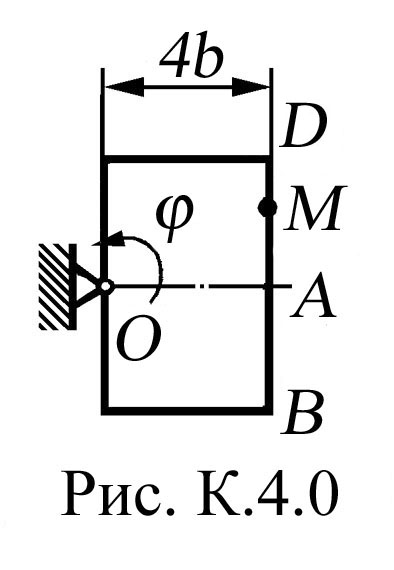
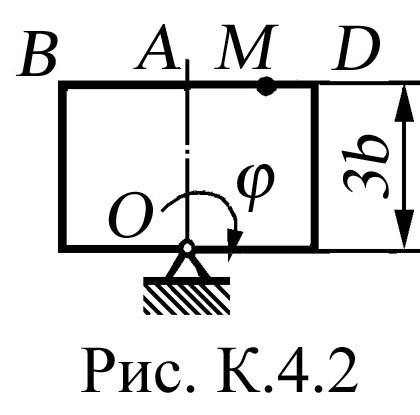
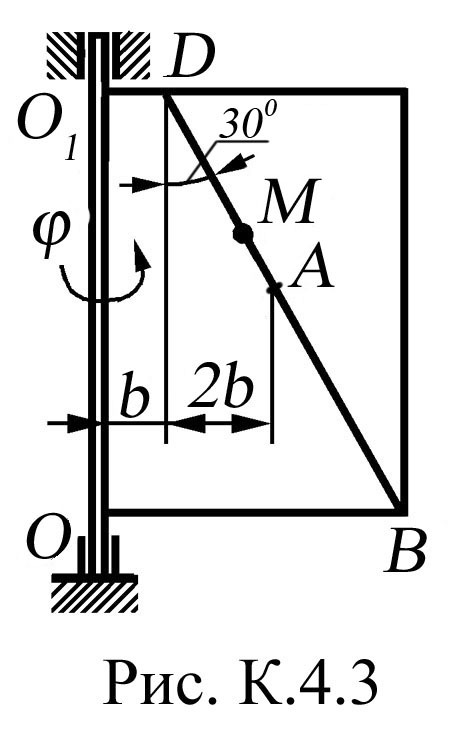
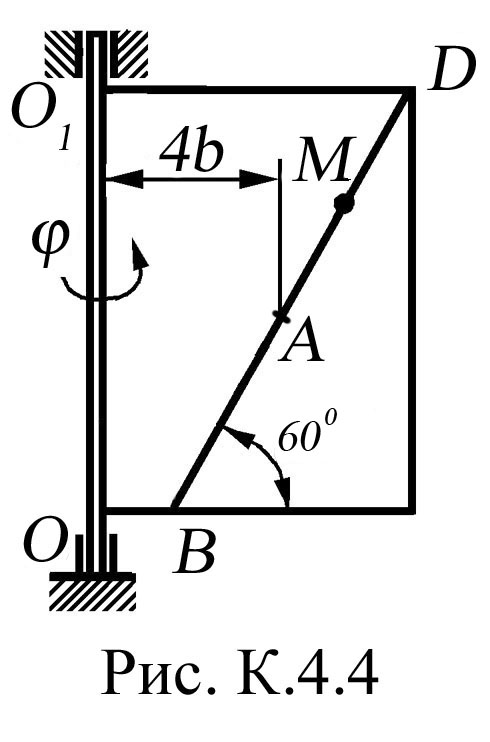
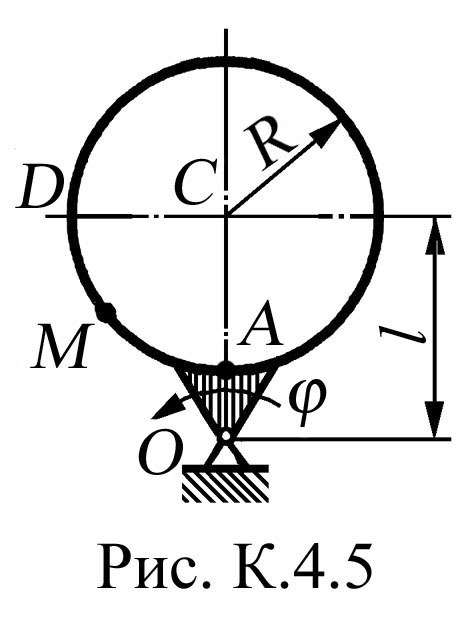
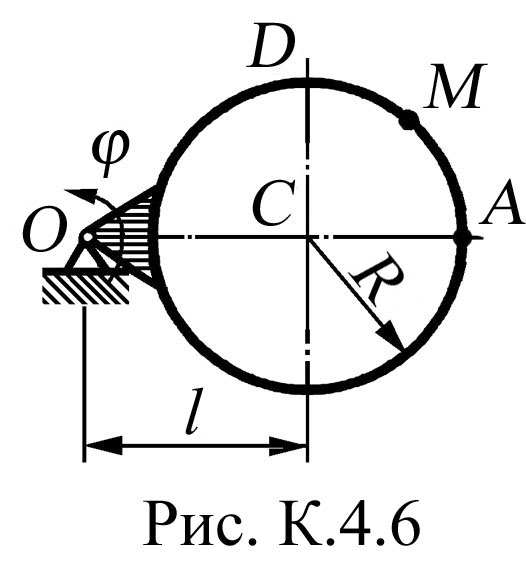
На рис. К.4.0, К.4.1, К.4.2, К.4.5, К.4.6 вісь обертання перпендикулярна до площини пластини та проходить через точку О (пластина обертається у своїй площині); на рис. К.4.3, К.4.4, К.4.7, К.4.8, К.4.9 вісь обертання ОО₁ лежить у площині пластини (пластина обертається в просторі).

По пластині вздовж прямої ВD (рис. К.4.0 - К.4.4) або по колу радіуса R (рис. К.4.5 - К.4.9) рухається точка М; закон її відносного руху, тобто залежність (S виражено в сантиметрах, t – у секундах), задано в таблиці 10. Умови задач К.4.0 – К.4.9, у таблиці 11. Умови задач К.4.0.А – К.4.9.А або в таблиці 12. Умови задач К.4.0.Б – К.4.9.Б (залежно від рівня складності) окремо для рис. К.4.0 - К.4.4 і для рис. К.4.5 - К.4.9. Там же задані розміри b i l. На рисунках точка М показана в положенні, при якому (при точка М знаходиться з протилежного боку від точки А).

Знайти абсолютну швидкість та абсолютне прискорення точки М у момент часу с.

Методичні вказівки

Задача К.4. – на складний рух матеріальної точки. Для розв’язання задачі необхідно скористатись теоремою про складання швидкостей і теоремою про додавання прискорень.

Перед початком розрахунків необхідно за даними задачі визначити, де знаходиться точка М на площині в момент часу с і показати матеріальну точку М у цьому положенні (а не в довільному положенні, яке показане на рисунках до задачі).

При розв’язанні задачі з рис. К.4.5 – К.4.9 числове значення R не підставляється до того часу, поки не будуть визначені положення матеріальної точки М у момент часу с і кут між радіусами СМ і СА у цей момент часу.

При розв’язанні задачі К.4 з використанням даних таблиці 10. Умови задач К.4.0 – К.4.9 студент отримує оцінку ”задовільно”. При розв’язанні задачі К.4 з використанням даних таблиці 11. Умови задач К.4.0.А – К.4.9.А студент отримує оцінку ”добре”. При розв’язанні задачі К.4 з використанням даних таблиці 12. Умови задач К.4.0.Б – К.4.9.Б студент отримує оцінку ”відмінно”.

Приклад 1 розв’язання задачі К.4. Перший рівень складності

Прямокутна пластина обертається навколо нерухомої осі за законом (рис. 27.15). Вісь обертання перпендикулярна до площини пластини та проходить через точку О (пластина обертається у своїй площині). По пластині вздовж прямої ВD рухається точка М; задано закон її відносного руху, тобто залежність (S виражено в сантиметрах, t – у секундах).