3.3. Зміст першого домашнього завдання

1. Провести структурний аналіз механізму.

2. Побудувати 12 положень механізму і траєкторію руху точки Е (схеми

І -VІ) і точки С (схеми VI-VII). Побудову проводити в масштабі.

3. Побудувати плани швидкостей та прискорень для двох заданих положень ведучої ланки ₁ і ₂.

4. Силовий аналіз плоских механізмів

Проводимо силовий аналіз заданого механізму в положенні ₂=90°.

Додатково задано: маси ланок m₁=4 кг; m₂=2 кг; m₃=6 кг; моменти інерції ланок відносно осі, що проходить крізь центр ваги ланок I_S1=2,1 кгм²; I_S2=3 кгм²; I_S3=0,8 кгм²; F_к.₀ = 50 Н.

4.1. Знаходження сил інерції та моментів сил інерції ланок механізму

Ланка 1. Так як ланка обертається рівномірно (₁=const; ₁=0), то система елементарних сил інерції точок ланки зводиться до головного вектору сил інерції, який прикладається в центрі ваги ланки:

H.

Ланка 2.

H;

Hм.

Момент замінюємо парою сил:

Н.

Ланка 3.

H;

Hм.

Момент замінюємо парою сил:

Н.

Головні вектори сил інерції та, головні моментитавраховують вплив прискореного руху ланок. Знак “─” у формулах означає, що силанаправлена протилежно прискоренню, а момент-протилежно кутовому прискоренню. Моменти сил інерціїтазамінюємо парами сил, які прикладені в кінцевих кінематичних парах відповідної ланки і спрямовані перпендикулярно вісі відповідної ланки.

Вага ланок буде:

Н;

Н;

Н.

4.2. Силовий аналіз групи Ассура (2 - 3)

Для силового дослідження механізму застосовують графоаналітичний та аналітичний методи. Широке розповсюдження набув кінетостатичний метод силового аналізу, який базується на принципі Даламбера. Суть цього методу: якщо до зовнішніх сил, які діють на ланки механізму додати сили інерції та моменти сил інерції ланок, то системою всіх цих сил можна розглядати таку, що знаходиться в стані рівноваги. За цієї умови геометрична сума векторів усіх сил, що діють у механізмі буде дорівнювати нулю, а невідомі сили можуть бути визначені методами статики.

Від’єднаємо заключну групу механізму та креслимо ії в масштабі ₁ (2-3) (рис. 1.7). Докладаємо до ланок групи сили ваги G₂ та G₃, сили інерції Ф_i2 та Ф_i3 (напрямок прикладання їх у бік, протилежний напрямку прискорення центру ваги. Точка прикладання цих сил – центр ваги ланки). Докладаємо моменти сил інерції, замінюючи їх парами сил та;та.

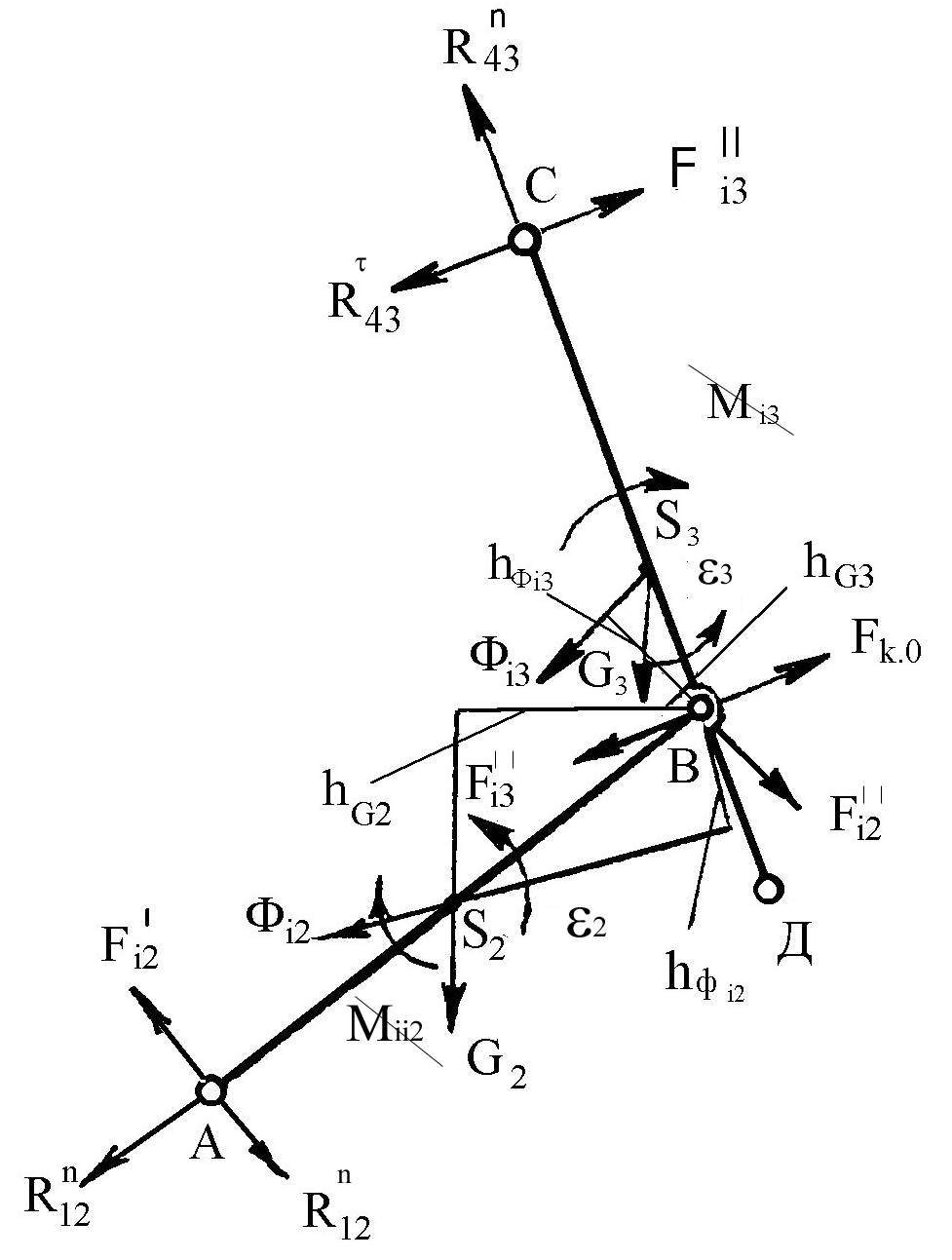
Рис. 1.7

Додаємо силу корисного опору F_ко у т. В протилежно вектору швидкості точки В.

Дію зруйнованих зв’язків кінематичних пар А та С замінюємо реакціями R₁₂ та R₄₃ .

Умовно зображаємо всі сили відрізками довжиною 20 мм. Оскільки напрямок цих реакцій невідомий, то замінюємо їх складовими, напрямки яких обираються довільно.

;

.

Тангенціальну складову знаходимо з рівняння рівноваги моментів сил, діючих на ланкуАВ відносно точки В.

М_В=0

,

де та- плечі дії сил – перпендикуляри, які опущені з точки В на лінію дії відповідної сили:

.

Значення АВ, h_G2, h_Фi2 беремо безпосередньо з малюнка (рис. 1.7) в мм:

.

Тангенціальну складову R^₄₃ знаходимо з рівняння рівноваги моментів сил, діючих на ланку ВС відносно точки В.

;

.

Значення ВС, h_G3, h_Фi3 беремо безпосередньо з малюнка (рис. 1.7) у мм.

.

Нормальні складові тазнайдемо побудовою замкненого багатокутника сил, що відповідає рівнянню рівноваги сил у векторній формі.

.

Будуємо план сил. Для цього з довільно обраної точки –р_F –полюсу плану сил - відкладаємо одну за одною всі відомі сили в такій послідовності: спочатку відомі сили другої ланки, потім відомі сили третьої ланки, а наприкінці невідомі сили третьої та другої ланок (рис.1.8).

Побудову плану сил виконуємо в масштабі:

Н/мм.

Проведемо вектори сил (рис.1.8.) ;;;;;;в сторону дії відповідної сили, при чому довжину векторів визначаємо в масштабі, тобто в мм:

;;;

; ;.

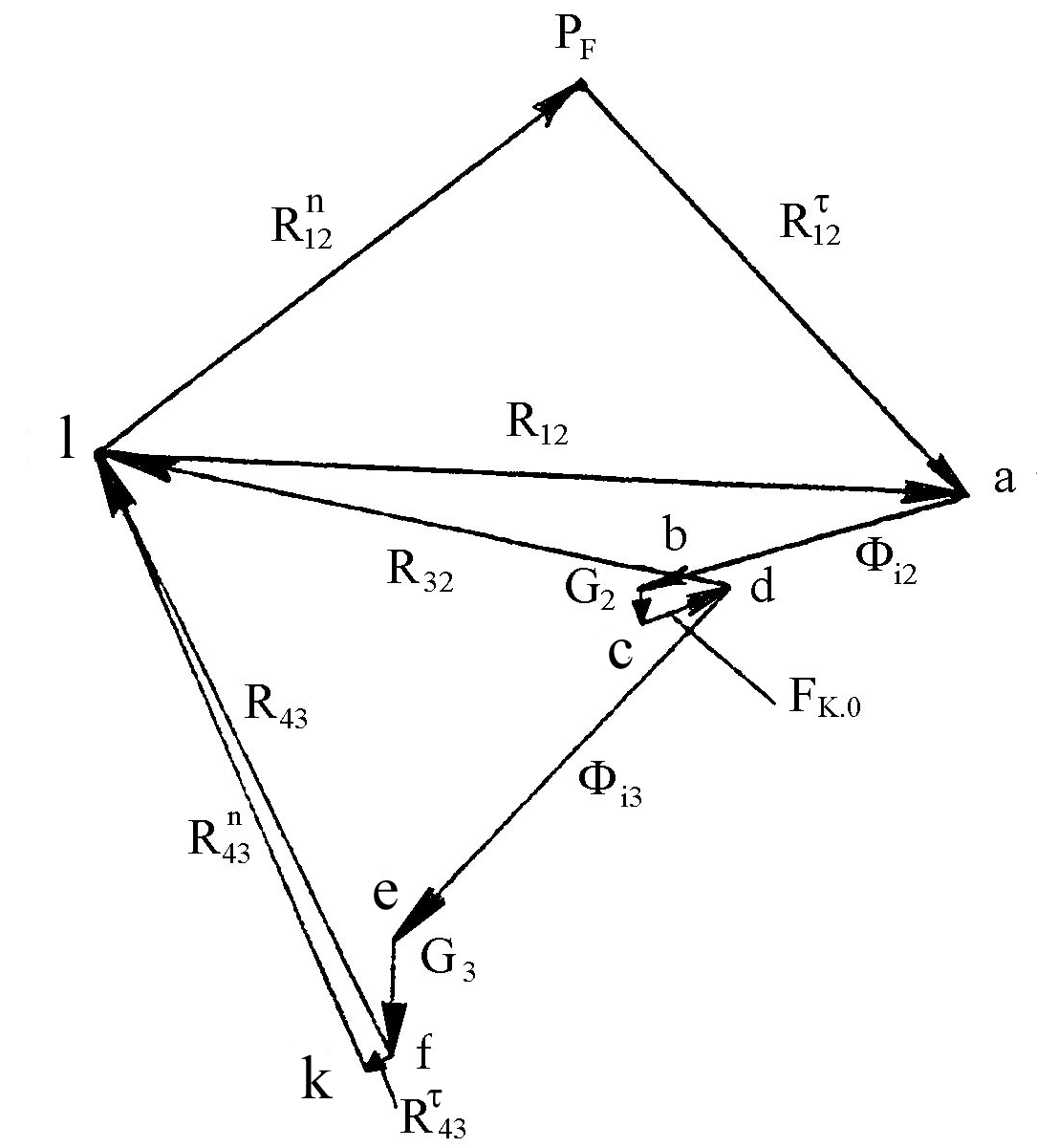
Рис. 1.8

Відклавши останню відому силу з т.р_F та точки К проведемо перпендикуляри, позначаючи напрямок нормальних складових реакцій та. Точку перетину цих перпендикулярів позначимо т.l. З'єднаємо точку f та точку l – отримаємо реакцію у масштабі_F, а точку l та точку а – реакцію у масштабі_F:

H.

H;

H;

H;

Невідому реакцію знайдемо замкнувши багатокутник сил, тобто, з’єднавши точкуd з точкою l плану сил.

H.