Історична довідка. Метод математичної індукції.

“Знання людей заслуговує ім’я Науки залежно

від того, яку роль має в ньому число”

/Е. Борель/

Як відомо, аксіоматична побудова будь-якої математичної теорії починається з переліку невизначених, основних понять (об’єктів і відношень) і аксіом, яким повинні задовольняти основні поняття.

Система аксіом натуральних чисел, якою зараз всі користуються, була запропонована італійським математиком і логіком кінця XIX ст., професором Турінського університету Джузеппе Пеано (1858-1932) у статті “Про поняття числа”, надрукованої у 1891р. Ось як сформулював Пеано свої п’ять аксіом, які лежать в основі визначення натурального числа.

1. 0 є натуральним числом.

2. Число, яке безпосередньо стоїть за натуральним числом є натуральне число.

3. 0 не стоїть ні за яким натуральним числом.

4. Будь-яке натуральне число слідує тільки за одним натуральним числом.

5. Аксіома індукції.

З аксіоматичної точки зору ми маємо справу з двома основними поняттями:

“натуральні числа” (об’єкт) і “безпосередньо слідує за ” (співвідношення). Ці поняття косвено визначаються системою аксіом.

Система аксіом натуральних чисел, яка пропонується зараз у сучасних працях науковців лише за формою трішечки відрізняються від аксіоматики Пеано.

Натуральні числа – це елементи будь-якої не порожньої множини N, у якої для деяких елементів a і b встановлено відношення “b слідує за a”, яке задовольняє слідуючим чотирьом аксіомам:

1. Існує натуральне число 1, яке безпосередньо не стоїть ні за яким натуральним числом, тобто для будь-якого a із N маємо a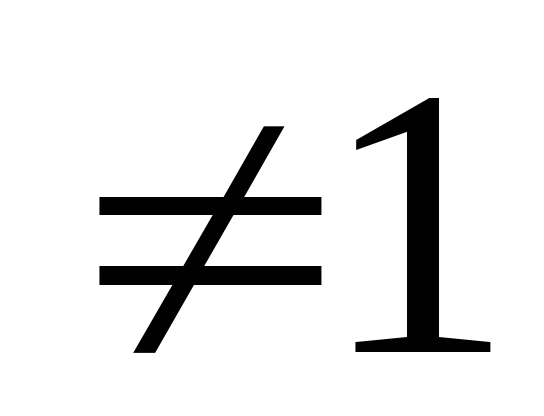^*(де a^* - число, яке безпосередньо слідує за a ).

2. Для кожного натурального числа a із N існує одне і тільки одне число a^*, яке безпосередньо слідує за a, тобто a=b a^*=b^*.

3. Будь-яке натуральне число, крім 1, безпосередньо слідує лише за одним натуральним числом, тобто, якщо a1, тоді з a^*=b^*a=b.

4. Аксіома індукції. Якщо множина M є підмножиною множини N натуральних чисел і :

а) одиниця міститься в М;

б) і разом з кожним числом а міститься в М слідуюче за ним число a^*, то множина М співпадає з множиною N.

Те, що у Пеано перший елемент є 0, а не 1, не має принципіального значення. У сьогоденні нуль вважають цілим, а не натуральним числом.

На основі аксіом 1 – 4 можна визначити арифметичні дії та побудувати всю арифметику натуральних чисел чисто дедуктивним шляхом.

Четверту аксіому називають аксіомою математичної індукції, тому що вона еквівалентна принципу математичної індукції, тобто на основі 4 можна довести слідуюче твердження: якщо деяка теорема Т(n) в якій йде мова про натуральні числа, вірна для n=1 і з того, що вона має місце при n=k (k – довільне натуральне число ), витікає, що вона вірна і для n=k+1, то теорема Т(n) вірна і для довільного натурального числа n.

Доведення.

Позначимо через М множину тих і тільки тих натуральних чисел, для яких теорема Т(n) має місце. Тоді за аксіомою 4 маємо:

1. 1М;

2. kМ(k+1)M.

Отже, M=N, тобто теорема Т(n) справедлива для довільного натурального числа n.

Звичайно за аксіому приймають саме принцип математичної індукції.

Принципом математичної індукції фактично користувалися ще деякі давньогрецькі вчені. Але вперше сформулював його у 1321р. французький філософ, математик, астроном Леві бен Гершону ( 1288 – 1344 ), більш відомий під прізвіщами Лев Герсонід, Ралбаг, метр Леон де Баньоль. Він жив у різних місцях Південної Франції.

Характеристика принципу математичної індукції є і у широко освідченого італійського математика XVIст. Ф. Мавроліко, перекладача Архімеда.

Метод доведень, що грунтується на принципі математичної індукції, називають методом математичної індукції. Доведення методом математичної індукції повинне складатися з двох самостійних теорем.

Теорема 1. Довести, що дане твердження справджується для n=1. Цю частину доведення називають базисом індукції – доведення істинності твердження А(1).

Теорема 2. Припустивши, що дане твердження правильне при n=k, де k – яке-небудь довільне натуральне число ( це припущення називають індуктивним припущенням ), доводимо, що твердження є правильним і для n=k+1. Ця частина доведення має назву індуктивний перехід або індуктивний крок.

Якщо обидва ці етапи проведено, то на підставі принципу математичної індукції твердження справедливе для всякого натурального n.

Дійсно, теорема 1 створює базу для проведення індукції, а теорема 2 дає право необмеженого автоматичного розширення цієї бази, право переходу від даного частинного випадку до дальшого.

Зауважуємо, що доведення методом математичної індукції безумовно вимагає доведення обох теорем 1 і 2, кожна з яких має своє особливе значення.

Спосіб доведення, який зараз називається методом математичної індукції, запропонували Блез Паскаль (1623 – 1663рр.) і Якоб Бернуллі (1654 – 1705рр.).

У “Трактаті про арифметичний трикутник ” Б. Паскаль доводить закон створення членів цього трикутника методом математичної індукції, після чого цей метод починає поступово притягувати увагу деяких вчених, окремо Я. Бернуллі.

Лише з другої половини XIXст. Після праць Больцано, Коші, Гауса, Абеля чисто індуктивні методи доведення утрачають значення у математиці. На перший план виходять дедукція і математична індукція.

Метод математичної індукції використовується і в експериментальних науках.