
- •Іі. Вектори
- •2.1. Вектори. Лінійні операції над векторами
- •Приклади для самостійного розв’язання
- •2.2. Розклад даного вектора за напрямками на прямій, на площині і в просторі
- •2.3. Лінійна залежність і лінійна незалежність системи векторів
- •2.4. Базис. Декартові система координат. Дії над векторами в координатній формі
- •Приклад для самостійного розв’язання
- •2.5. Прямокутна декартова система координат
- •3°. Два вектори рівні, якщо у них рівні відповідні координати.
- •Координати вектора, заданого початковою і кінцевою точками
- •Приклади для самостійного розв’язання
- •2.6. Умова колінеарності двох векторів. Поділ відрізка в даному відношенні
- •Задачі для самостійного розв’язання
- •2.8. Скалярний добуток векторів
- •Задачі для самостійного розв’язання
- •2.9. Векторний добуток двох векторів
- •Деякі застосування векторного добутку
- •Приклади для самостийного розв’язання
- •2.10. Мішаний добуток трьох векторів
- •Приклади для самостійного розв’язання:
Приклади для самостийного розв’язання
Спростити вираз
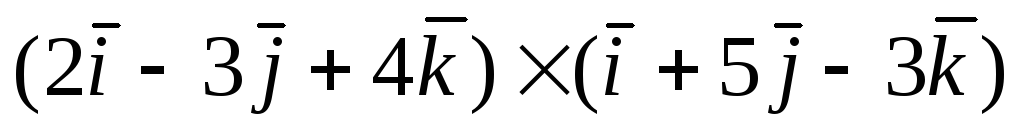 за
допомогою властивостей векторного
добутку та таблиці векторного добутку
ортів. Перевірити результат за формулою
(1).
за
допомогою властивостей векторного
добутку та таблиці векторного добутку
ортів. Перевірити результат за формулою
(1).Дано вектори
 і
і .
Знайти: 1)
.
Знайти: 1) 2) площу паралелограма, побудованого
на векторах
2) площу паралелограма, побудованого
на векторах і
і .
Побудувати паралелограм на векторах
.
Побудувати паралелограм на векторах і
і та
вектор
та
вектор .
.Дано точки А(2,-4,3), В(2,3,-1) і С(-1,4,3). Обчислити площу трикутника АВС.
Дано вектори
 і
і .
Знайти векторний добуток
.
Знайти векторний добуток двома
способами: 1) перетворенням даного
виразу за допомогою властивостей
векторного добутку; 2) вираженням
векторів
двома
способами: 1) перетворенням даного
виразу за допомогою властивостей
векторного добутку; 2) вираженням
векторів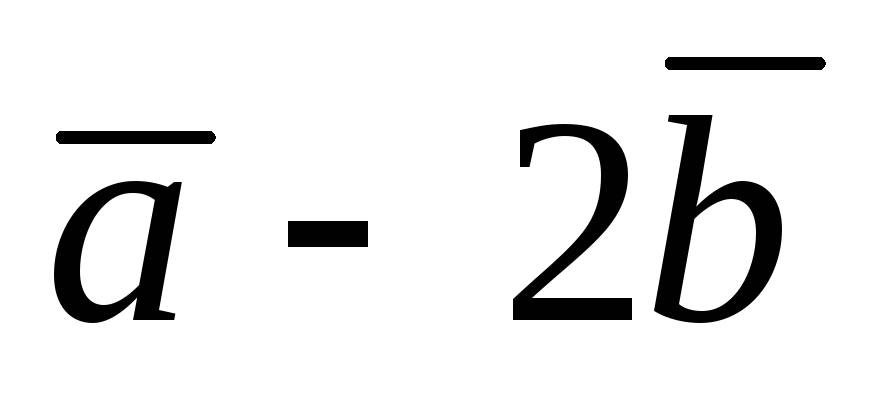 і
і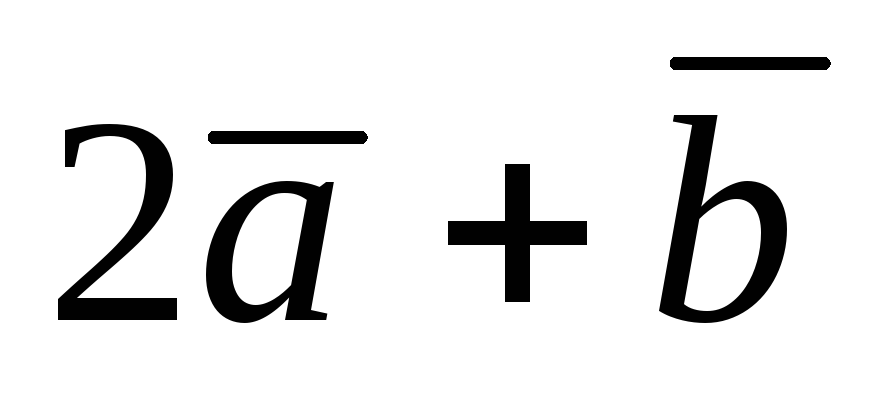 через орти і наступним застосуванням
формули (1).
через орти і наступним застосуванням
формули (1).Знайти орт
 ,
перпендикулярний векторам
,
перпендикулярний векторам і
і .
.Сила
 прикладена до точки А(1,-5,3). Знайти її
момент відносно початку координат.
прикладена до точки А(1,-5,3). Знайти її
момент відносно початку координат.Сила
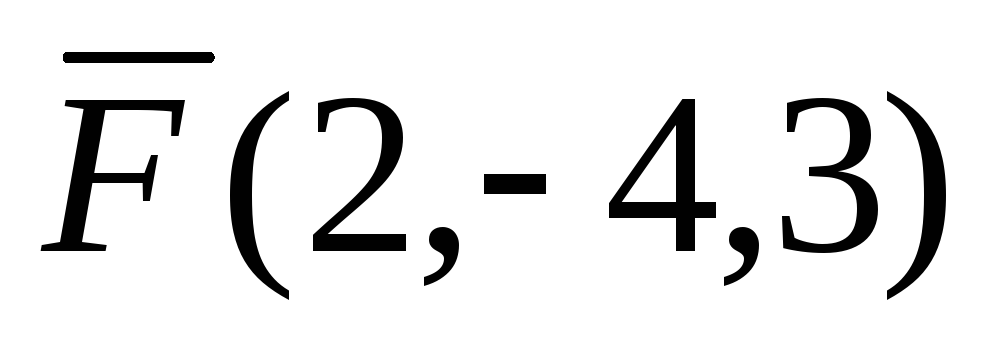 прикладена до точки А(2,6,-1). Знайти її
момент відносно точки В(6,-2,5).
прикладена до точки А(2,6,-1). Знайти її
момент відносно точки В(6,-2,5).Дано три сили
 ,
, ,
, ,
прикладені в точці А(-2,3-3). Знайти момент
рівнодійної цих сил відносно точки
В(1,2,-2), а також величину цього моменту.
,
прикладені в точці А(-2,3-3). Знайти момент
рівнодійної цих сил відносно точки
В(1,2,-2), а також величину цього моменту.Дано трикутник А(8,-10,12), В(6,-14,16) і С(16,-4,16). Знайти довжину висоти
 ,
яка проведена з вершини С.
,
яка проведена з вершини С.
Відповіді:
1.
![]() .2.
.2.
![]() .
3.
.
3.
![]() .
.
4.
![]() .
5.
.
5.
![]() .
.
6.
![]() .
7.
.
7.
![]() .
.
8.
![]() .
9.
10.
.
9.
10.
2.10. Мішаний добуток трьох векторів
Означення.
Мішаним
(векторно-скалярним) добутком трьох
векторів
![]() (позначається
(позначається![]() )
називається скалярна величина, що
дорівнює скалярному добуткові вектора
)
називається скалярна величина, що
дорівнює скалярному добуткові вектора![]() на вектор
на вектор![]() .
.
Знайдемо
об’єм
паралелепіпеда побудованого на векторах
![]() (див. рис. 24).
(див. рис. 24).
![]()

Рис. 24
Таким
чином, об’єм
паралепіпеда, побудованого на векторах
![]() ,
зведених до однієї точки О, дорівнює з
точністю до знаку мішаному добутку цих
векторів.
,
зведених до однієї точки О, дорівнює з
точністю до знаку мішаному добутку цих
векторів.
Формула мішаного добутку в координатній формі може бути отримана при послідовному виконанні дій


Приклад.
Знайти об’єм
паралепіпеда, побудованого на векторах
![]() .
.
Відповідь:
![]() (од.куб.)
(од.куб.)
Властивості мішаного добутку векторів.
1.
Вектори
![]() компланарні тоді і тільки тоді, коли їх
мішаний добуток дорівнює нулю (
компланарні тоді і тільки тоді, коли їх
мішаний добуток дорівнює нулю (![]() ),
тобто
),
тобто
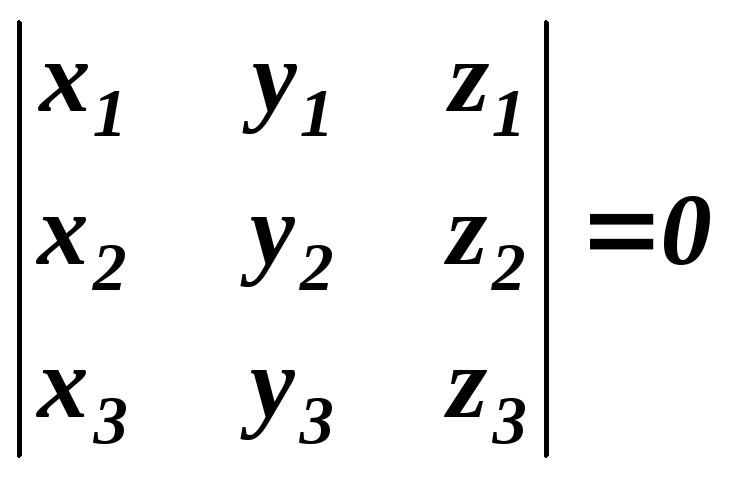 (3)
(3)
умова компланарності трьох векторів.
![]()
Властивості 2 і 3 випливають з того, що парна перестановка рядків визначника не змінює його знак, а непарна змінює на протилежний.
Об’єм
піраміди,
побудованої на векторах
![]() дорівнює
дорівнює![]() об’єму
відповідного паралелепіпеда, тобто
об’єму
відповідного паралелепіпеда, тобто

З
двох знаків «![]() »
вибираємо такий, щоб об’єм
V
був
невідємним.
»
вибираємо такий, щоб об’єм
V
був
невідємним.
Приклад. Знайти об’єм піраміди з вершинами в точках А(0,-5,1), В(4,1.0), С(2,5,2) і S(3,-1,7).
Розв’язання.
Знайдемо вектори
![]()
![]()
![]()

Обчислимо мішаний добуток векторів

![]() ,
,
![]() .
.
Приклади для самостійного розв’язання:
Дано вектори
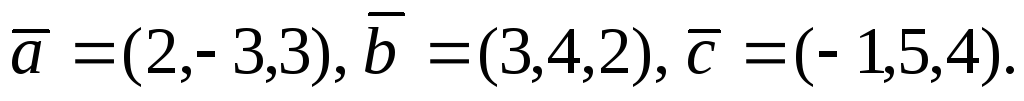 Необхідно:
1) Знайти спочатку векторний добуток
Необхідно:
1) Знайти спочатку векторний добуток ,
а тоді скалярний
,
а тоді скалярний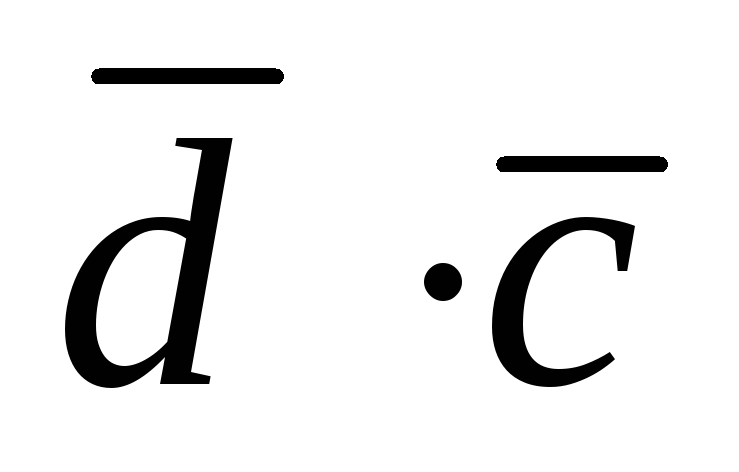 ;
2) обчислити
;
2) обчислити за формулою (2); 3) обчислити
за формулою (2); 3) обчислити .
.Знайти об’єм паралелепіпеда, побудованого на векторах
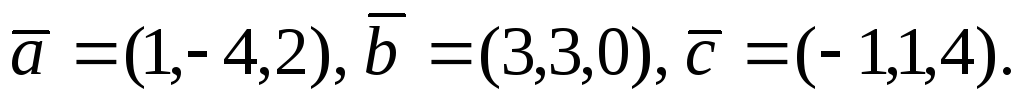
Знайти об’єм піраміди побудованої на векторах
 ,
, ,
, .
.Обчислити об’єм піраміди з вершинами в точках А(2,-3,5), В(0,2,1), С(-2,-2,3) і D(3,2,4).
Обчислити висоту AM піраміди АВСD, яка опущна з точки А на площину BCD, якщо вершини піраміди містяться в точках А(1,1,1), В(2,0,2), С(2,2,2), Д(3,4,-3).
Встановити, чи компланарні вектори:
1)
![]()
2)
![]()
З’ясувати, чи лежать точки А(3,0,0), В(1,1,8), С(2,1,6), D(3,1,4) в одній площині.
Довести, що вектори
 лінійно залежні та виразити лінійно
лінійно залежні та виразити лінійно через
через і
і .
.
Відповіді:
1. 111.
2.
72.
3.
12.
4.
6.
5.
![]() .
6.
1)
так; 2) ні.
.
6.
1)
так; 2) ні.
7.
Так.
8.
![]() .
.
