
- •Іі. Вектори
- •2.1. Вектори. Лінійні операції над векторами
- •Приклади для самостійного розв’язання
- •2.2. Розклад даного вектора за напрямками на прямій, на площині і в просторі
- •2.3. Лінійна залежність і лінійна незалежність системи векторів
- •2.4. Базис. Декартові система координат. Дії над векторами в координатній формі
- •Приклад для самостійного розв’язання
- •2.5. Прямокутна декартова система координат
- •3°. Два вектори рівні, якщо у них рівні відповідні координати.
- •Координати вектора, заданого початковою і кінцевою точками
- •Приклади для самостійного розв’язання
- •2.6. Умова колінеарності двох векторів. Поділ відрізка в даному відношенні
- •Задачі для самостійного розв’язання
- •2.8. Скалярний добуток векторів
- •Задачі для самостійного розв’язання
- •2.9. Векторний добуток двох векторів
- •Деякі застосування векторного добутку
- •Приклади для самостийного розв’язання
- •2.10. Мішаний добуток трьох векторів
- •Приклади для самостійного розв’язання:
2.6. Умова колінеарності двох векторів. Поділ відрізка в даному відношенні
1.
Нехай ненульові вектори
![]() колінеарні,
колінеарні,![]() ,
тобто існує таке число
,
тобто існує таке число![]() ,
що
,
що![]() .
В координатній формі:
.
В координатній формі:
![]()
![]() (1)
(1)
Отже, умовою колінеарності двох векторів є пропорційність їх відповідних координат.
Приклад. Чи колінеарні вектори
![]() ?
?
Розв’язання.
За умовою
![]() =(1,2,-3),
=(1,2,-3),
![]() =(-3,-6,9),
а за
=(-3,-6,9),
а за
формулою
(1) маємо
![]() ,
або ще можна записати
,
або ще можна записати![]() .
.
2.
Поділ
відрізка в даному відношенні. Знайти
координати точки М(х,у,z),
яка ділить відрізок
![]()
![]() в заданому відношенні
в заданому відношенні![]() (рис. 14), якщо відомі координати точки
(рис. 14), якщо відомі координати точки![]() і
і![]() ,
тобто:
,
тобто:
![]()

![]()

М

![]()

Рис.14
Розглянемо
вектори
![]() і
і![]() .
Оскільки
.
Оскільки![]() і
і![]() ,
то згідно з умовою (1) колінеарності
векторів маємо
,
то згідно з умовою (1) колінеарності
векторів маємо
![]()
![]()
![]()
Зокрема,
якщо точка М ділить відрізок пополам,
то
![]() і координати середини відрізка:
і координати середини відрізка:
![]()
Задача. Знайти координати центра мас трикутника АВС, у вершинах А(4,0,-2), В(-2,6,4), С(7,-3,4) якого зосереджені одиничні точкові маси.
Розв’язання. Побудуємо вершини трикутника за їх координатами (див. рис.) А(4,0,-2), В(-2,6,4), С(7,-3,4).

Знайдемо середину відрізка АВ, це точка М – основа медіани:
![]() ,
,
![]()
![]() M(1,3,1).
M(1,3,1).
Відомо, що центр трикутника має знаходитись на перетині медіан, а медіани, перетинаючись, діляться у відношенні 2:1, починаючи від вершини, тобто
![]() ,
,
![]() ,
,
![]() .
.
Отже, Р(3,1,2)- центр мас трикутника АВС.
Задачі для самостійного розв’язання
Довести, що чотирикутник з вершинами А(3,2,-3), В(2,4,6), С(8,3,4), D(9,1,-5) є паралелограм.
Показати, що точки А(3,4,1), В(1,0,-1) і С(-2,-6,-4) лежать на одній прямій.
Дані точки А(-3,6,1) і В(7,-9,-4). Знайти координати точок С, D, Е, i F, які ділять відрізок АВ на п’ять рівних частин.
Знайти координати кінців P і Q відрізка, який точками М(3,1,3) і N(6,-1,1) розділений на три рівні частини.
Відповіді: 3. С(-1,3,0), D(1,0,-1), E(3,-3,-2), F(5,-6,-3)
4. P(0,3,5), Q(9,-3,-1).
2.7. Кут між векторами. Проекція вектора на вісь. Властивості проекцій
1.
Кут між векторами.
Нехай задані ненульові вектори
![]() .
Зведемо ці вектори до спільної точки О
і в напрямках векторів
.
Зведемо ці вектори до спільної точки О
і в напрямках векторів![]() проведемо з точки О промені (див. рис.
15).
проведемо з точки О промені (див. рис.
15).
Менший
з кутів, які утворені цими променями
називається кутом
між векторами
![]() і позначається
і позначається![]() .
.
Кут
між вектором
![]() і нульовим вектором не означається.
і нульовим вектором не означається.
Очевидно,
що якщо
![]() ,
то
,
то![]() ;
Якщо ж
;
Якщо ж![]() то
то![]() .
.
Вправи.
1).
Знайти
![]() ,
,![]() ,
,![]() .
.
2).
Нехай
![]() .
Знайти
.
Знайти![]()
![]() .
.

Рис. 15
3).
Розглянемо
рівнобедренний прямокутний трикутник
АВС, де
![]() .
Знайти
.
Знайти![]()
![]()
![]()
![]()
Відповіді:
![]()
2.
Проєкцію
вектора
![]() на вісь
на вісь![]() (позначається
(позначається![]() )
називається довжина відрізка, який
сполучає проекції на цю вісь початку і
кінця вектора, взята зі знаком « + », якщо
кут між вектором і віссю гострий і знаком
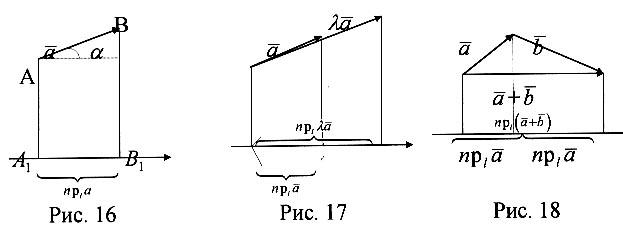
« - », якщо цей кут тупий (рис. 16).
)
називається довжина відрізка, який
сполучає проекції на цю вісь початку і
кінця вектора, взята зі знаком « + », якщо
кут між вектором і віссю гострий і знаком
« - », якщо цей кут тупий (рис. 16).
Очевидно,
що коли
![]() ,
то
,
то![]() =0,
і навпаки.
=0,
і навпаки.
Основні властивості проекцій:
1.
![]() =
=![]() (рис. 16);
(рис. 16);
2.
![]() =
=![]() (рис. 17);
(рис. 17);
3.
![]() =
=![]() +
+![]() (рис. 18).
(рис. 18).
Властивість 3 виконується для суми скінченного числа векторів.
2.8. Скалярний добуток векторів
Означення.
Скалярним
добутком
![]() двох векторів
двох векторів
![]() (позначається
(позначається![]() ) називається число рівне добуткові
модулів цих векторів, помноженому на
косинус кута між ними:
) називається число рівне добуткові
модулів цих векторів, помноженому на
косинус кута між ними:
![]() .
(1)
.
(1)
На основі властивості 1 проекцїї вектора рівність (1) запишеться:
![]() (2)
(2)
У
фізиці робота А сталої сили
![]() при прямолінійному переміщенні вздовж
вектора шляху
при прямолінійному переміщенні вздовж
вектора шляху
![]() знаходиться як скалярний добуток цих
векторів:
знаходиться як скалярний добуток цих
векторів:
![]()
Основні властивості скалярного добутку.
![]() Скалярний добуток комутативний
Скалярний добуток комутативний
![]() .
.
Випливає із (1).
![]() Числовий множник
Числовий множник
![]() можна виносити за знак скалярного
добутку:
можна виносити за знак скалярного
добутку:
![]() .
.
![]() Для
довільних векторів
Для
довільних векторів
![]()
![]() .
.
![]() Скалярний добуток двох векторів
Скалярний добуток двох векторів
![]() дорівнює нулю (
дорівнює нулю (![]() )
тоді і тільки тоді, коли один із них є
нульовим вектором, або коли ці вектори
перпендикулярні
)
тоді і тільки тоді, коли один із них є
нульовим вектором, або коли ці вектори
перпендикулярні![]() .
.
Таблиця
скалярного множення ортів.
Згідно означення (1)
![]() ,
аналогічно
,
аналогічно![]() ,
а за властивістю (4)
,
а за властивістю (4)![]() .
.
Отже, скалярний добуток одноіменних ортів дорівнює одиниці, а різноіменних - 0.
Скалярний
добуток векторів в координатній формі.
Якщо
![]() ,
то
,
то![]() .
.
Дійсно,
за допомогою властивостей
![]() маємо
маємо

Оскільки добуток одноіменних ортів дорівнює 1, а різноіменних – 0, то отримуємо формулу скалярного добутку у координатній формі:
![]() .
(3)
.
(3)
Приклад
1. Знайти
скалярний добуток векторів
![]() і
і
![]() .
.
Розв’язання : За формулою (3) маємо:
![]() .
.
Приклад
2. Задані
точки А(3,2,3),
В(1,-4,3), С(-4,5,1).
Знайти скалярний добуток векторів
![]() .
.
Розв’язання
.
Спочатку
знайдемо вектори
![]()
![]()
За формулою (3) маємо
![]() .
.
Довжина вектора.Якщо в
(1)![]() ,
то
,
то
![]()
Відстань
між двома точками.
![]() і
і![]() знаходиться як довжина вектора
знаходиться як довжина вектора![]() за формулою (4):
за формулою (4):
![]()
Косинус кута між двома векторами отримаємо із формули (1) із врахуванням (3) і (4):

Приклад
3.
Задані точки
![]() .
Для паралелограма, побудованого на
векторах
.
Для паралелограма, побудованого на
векторах![]() і
і
![]() обчислити:
1)довжини сторін, тобто
обчислити:
1)довжини сторін, тобто
![]() і
і
![]() ;
2) косинус та синус, кута
;
2) косинус та синус, кута
![]() ;
3) площу.
;
3) площу.
Розв’язання.
Знаходимо
вектори
![]()
![]() тоді:
1)
тоді:
1)
![]() ,
,![]() .
2)
.
2)![]()
![]() (кут
(кут![]() - тупий ),
- тупий ),![]()
![]() .
3)
.
3)![]()
![]() .
.
Приклад
4.
Знайти модуль вектора
![]() ,
якщо
,
якщо
![]() .
.
Розв’язання.
За
формулою (4)
![]() .Знаходимо
.Знаходимо
![]()
![]() ,
,
тоді
![]() .
.
Умова
перпендикулярності двох ненульових
векторів
![]() випливає із властивості 4
і формули (3)
випливає із властивості 4
і формули (3)
![]()
Проекція вектора на вектор знаходиться із врахуванням (3) і (4):


Теорема.
Декартові прямокутні координати
![]() вектора
вектора![]() в базисі
в базисі
![]() є його проекціями на відповідні осі
координат.
є його проекціями на відповідні осі
координат.
Дійсно, згідно з (9) маємо
![]()
Напрямними
косинусами вектора
![]() називаються косинуси кутів
називаються косинуси кутів![]() ,
утворених між вектором
,
утворених між вектором![]() та координатними осями ОХ, ОУ, ОZ
(див. рис. 19)
та координатними осями ОХ, ОУ, ОZ
(див. рис. 19)

Приклад.
Знайти напрямні косинуси вектора
![]() та значення виразу
та значення виразу![]() .
.
Розв’язання.
![]()
![]()
![]() .
.
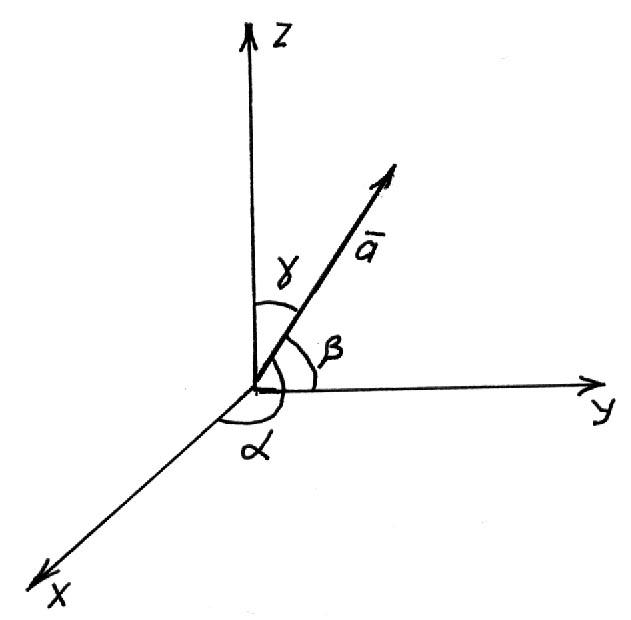
Рис. 19
Легко
перевірити, що для
довільного вектора
![]()
![]()
![]()
Напрямні
косинуси вектора
![]() повністю визначають напрямок вектора
і є координатами одиничного вектора
повністю визначають напрямок вектора
і є координатами одиничного вектора![]() ,
щозбігається
за напрямком з
,
щозбігається
за напрямком з
![]() ,
тобто:
,
тобто:
![]()
