3°. Два вектори рівні, якщо у них рівні відповідні координати.

(х₁=х₂, у₁=у₂, z₁=z₂).

Приклад. Довести:

1) що вектори = (3, -7, 10) і : рівні, якщо ,

де = (-5, -3, 1) і = (8, -4, 9);

2) що вектор = (8, -4, 7) дорівнює вектору = ,

де = (1, 1, -4),=(-2, 2, -5).

Виконати самостійно. Побудувати вектори ,,,. За координатами векторівіта за рисунком упевнитись, що іє діагоналями паралелограма, побудованого на векторахі.

Координати вектора, заданого початковою і кінцевою точками

Нехай вектор , заданий початковою точкоюі кінцевою, тоді (рис. 13) можна знайти його координати.

Рис. 13

Дійсно,

Висновок. Щоб знайти кординати вектора , заданого початковою точкою і кінцевою точкою , необхідно від координат його кінця відняти відповідні координати його початку

(1)

Приклади. 1. Знайти координати вектора , якщо (-1,2,3), (2,1,4).

Розв’язання. За формулою (1) маємо

=(2-(-1),1-2,4-3)=(3,-1,1).

Приклад 2. Початок вектора збігається з точкою. Знайти точку, з якою збігається кінець вектора.

Розв’язання. Відповідно до формули (1) для вектора маємо

(3,1,-5) = .

Враховуючи властивість 3^о із 2.4 запишемо

,

, .

Таким чином знаходимо точку N(1,8,-4).

Приклад 3. Упевнитись, що система векторів утворює базис, та знайти координати векторав цьому базисі, якщо відомі в прямокутній системі координати цих векторів , , , .

Розв’язання. Згідно означення (див. 2.4) вектори утворюютьбазис, якщо вони лінійно незалежні, тобто їх лінійна комбінація (де ), тільки тоді, коли.

Перевіримо це, скориставшись властивостями 1^о-3^о із 2.4:

Прирівнюючи відповідні координати, отримуємо систему:

Визначник цієї системи

Всі допоміжні визначники бо в кожному з них є нульовий стовпець із вільних членів однорідної системи. Отже, згідно формул Крамераі, таким чином, вектори- лінійно незалежні, а, значить, утворюють новий базис.

Звернемо увагу, що елементи стовпців визначника збігаються з відповідними координатами векторів.

Висновок. Якщо визначник, утворений з координат векторів ,відмінний від нуля, то ці вектори лінійно незалежні, тобто утворюють базис.

Тепер знайдемо координати вектора у базисі , тобто знайдемо числа такі, що виконується рівність

Повторюючи попередні перетворення маємо

Прирівнюючи відповідні координати у лівій і правій частинах рівності, отримаємо систему, яку зручніше розвязати алгебраїчним додаванням:

.

Із

Таким чином, при отримаємо .

Приклади для самостійного розв’язання

1. Нарисувати паралелограм, побудований на векторах і. Знайти: а) вектор; б) точку- вершину паралелограма, якщо відомі точки.

2. Дано вектори . Знайти вектори: а),.

3. Побудувати піраміду ABCD та знайти вектори , якщо відомі точкиА(3,6,3) В(1,-5,2), С(-4,0,1), D(-1,1,7).

4. Дано вектори Довести, що вектори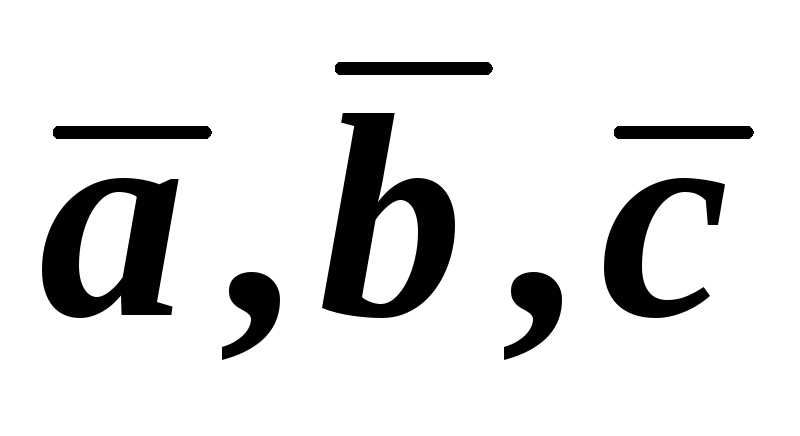утворюють базис. Знайти розклад векторау цьому базисі.

5. Для векторів та чиселперевірити властивості§2.1, де порядковий номер прізвища студента у груповому журналі.

Відповіді : 1.

2. a) б)

3. .

4. .