2.4. Базис. Декартові система координат. Дії над векторами в координатній формі

Означення. Система лінійно незалежних векторів простору, за якими можна розкласти довільний вектор, називається базисом цього простору.

Так з теореми 3 випливає, що довільні три некомпланарні вектори утворюють в тривимірному просторі базис, за яким, згідно з формулою(2) і зауваження до неї, можна єдиним чином розкласти довільний вектор простору. Векториякі утворюють базис називаютьсябазисними.

Будемо вважати, що базисні вектори зведені до заданої О.

Означення. Сукупність базісу спільної точки О називаютьдекартовою системою координат(див. рис. 11 у 2.3). Точка О називається початком координат.

Іноді таку систему називають косокутною.

Числа , про які згадувалось у 2.3, називають координатами вектора у заданому базисі , пишуть:

Аналогічно, на площині базис утворюють всякі два неколінеарні вектори, а всякий компланарний з ними може бути розкладений за цим базисом.

Базисним вектором на прямій лінії може бути всякий ненульовий вектор.

Із властивостей лінійних операцій над векторами випливає, що при додаванні і відніманні векторів в даному базисі додаються і віднімаються їх відповідні координати, а при множенні вектора на число множаться на це число координати вектора, тобто

Вектори рівні, коли вони мають рівні відповідні координати.

Приклад. У деякому базисі задані своїми координатами вектори Розкласти векторза базисом, який утворений із векторіві.

Розв’язання. Розклад вектора за базисомімає вигляд

= + β,

де числа іβ – невідомі. Щоб їх знайти підставимо в останню рівність координати векторів ,і, а тоді скористаємось властивостями 1⁰ і 2⁰:

(2,1) + β(3,4) = (-1,2)

(2 ,) + (3β, 4β) = (-1,2)

(2+ 3β,+ 4β) = (-1,2)

За властивістю 3⁰ про рівність векторів отримаємо систему рівнянь

-5β = -5, β = 1, ά = -2.

Отже, =-2+.

Приклад для самостійного розв’язання

1.У деякому базисі дані вектори =(-1,3,2) і= (0,1,4). За допомогою властивостей 1⁰ і 2⁰ обчислити координати таких векторів: а) +; б)-; в)(+2); г) (- 2) ; д) 2+ 3.

Відповіді. а) (-1,4,6); б) (-1,2,-2); в)

г) д) (-2,9,16) .

2.5. Прямокутна декартова система координат

Серед декартових систем найбільш поширеною є прямокутна системої координат.

Розглянемо три взаємно перпендикулярні осі ОХ, ОУ, ОZ із спільним початком в точці О - початком координат. Вісь ОХ називається віссю абсцис, ОУ - вісь ординат, ОZ - вісь аплікат (див. рис. 12,а).

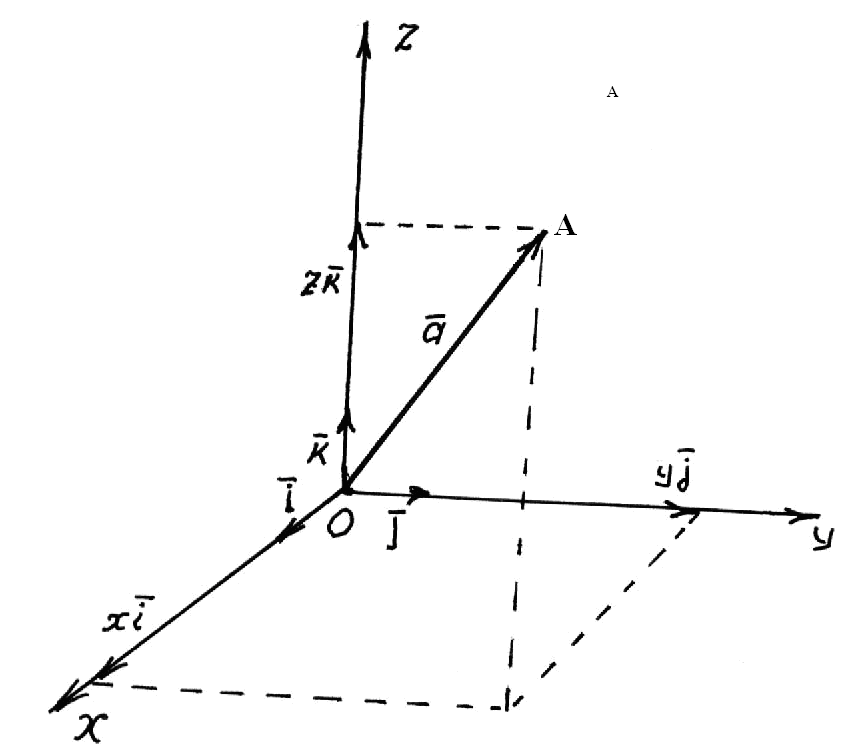
Рис. 12,а

Замість довільних базисних векторів зручніше взяти одиничні вектори, напрямлені відповідно вздовж осей ОХ, ОУ, ОZ. Такивектори називаються ортами, а утворений ними базис називається ортонормованим, . Вектор, який називається радіусом-вектором точкиА(х,у,z) в базисі-векторів , має розклад

Очевидно, що довільна точка А(х,у,z) в заданій системі координат одназначно визначається своїм радіусом-вектором , а координати точки є координатами її радіуса-вектора.

Звернемо увагу на такий факт. Якщо у попередніх параграфах під виразом “дано вектор” ми розуміли його графічне (геометричне) зображення, то тепер вираз “дано вектор” потрібно сприймати як задання трійки упорядкованих чисел (х, у, z) – координат вектора.

Якщо раніше лінійні дії над векторами здійснювались графічно, то тепер ці операції можна виконувати аналітично, не користуючись рисунком.

Сформулюємо лінійні дії ще раз (див. 1°-3°, § 2.4).

1°. Щоб додати(відняти) два вектори необхідно додати (відняти) їх відповідні координати, тобто

Приклад. Знайти суму векторів тазаданих на площиніХОУ.

Розв’язання. Відповідно до правила 1° маємо

Побудуємо ці вектори: .

Рис. 12,б

З рис. 12, б бачимо, що чотирикутник ОАВС – паралелограм. Координати вектора ==(6, 3) ми спочатку отримали шляхом обчислень (аналітично), без допомоги рисунка. Рисунок тільки підтверджує правило паралелограма при додаванні векторів, тому рисунками надалі користуємось для наочності.

2°. Щоб помножити вектор на число, необхідно кожну з його координат помножити на це число:

= (λх, λу, λz),

Приклад. Дано вектор =(1,-2, 2). Знайти

Розв’язання. Згідно з правилом 2° маємо:

(-2, 4, -4),

Рис. 12, в.

Геометричне зображення див на рис. 12, в.