Приклади для самостійного розв’язання

1. За даними векторами іпобудувати такі вектори: 1); 2) ; 3)

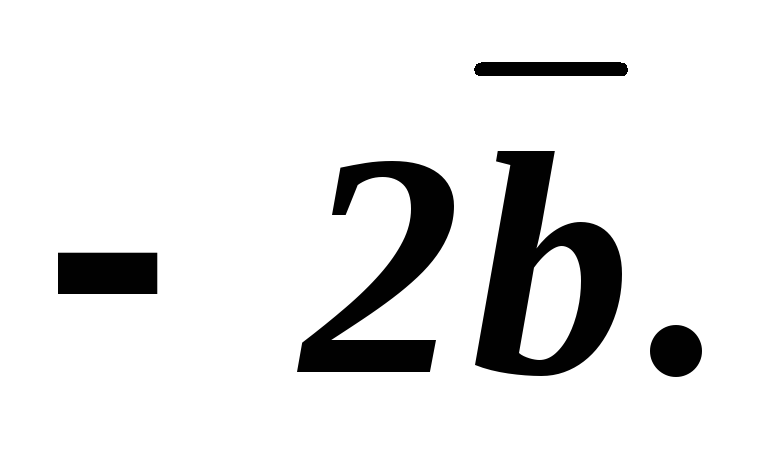
2. У паралелограмі АВСD задані вектори ,. Виразити черезвектори.

3. У трикутнику АВС проведені медіани АК, ВL і СМ. Визначити вектори через вектори.

4. У трикутнику АВС сторона АВ розділена точками D і F на три рівні відрізки: AD = DF = FB. Знайти вектори , якщо.

5. У трикутнику АВС проведені медіани AD, BE і CF. Довести, що

Відповіді. 2.

3. ;

4.

2.2. Розклад даного вектора за напрямками на прямій, на площині і в просторі

Означення. Вектор (1) називається лінійною комбінацієювекторів, де-деякі числові множники.

У виразі (1) вектор отримано в результаті лінійних операцій над векторами. Іноді говорять, що векторлінійно виражається через вектори. Вираз (1) називають такожрозкладом вектора по системі векторів.

В необхідності розкладу вектора за даними напрямками можна переконатись на такому прикладі.

Дві опори (рис. 9) утримують вантаж під дією сили земного тяжіння . Необхідно знайти зусилля на кожну з опор.

Рис. 9

Для розв’язання задачі розкладемо вектор за правилом паралелограма на складовіі,=+, які напрямлені вздовж опор. Величини зусильможна знайти за допомого теореми синусів, розглядаючи паралелограм АВСО, в якому відома діагональі кутиі, які вона утворює зі сторонами ОВ і ОС.

Пропонуємо самостійно переконатись, що

Тепер перейдемо до лінійного вираження вектора за напрямками в більш загальній формі: на прямій, на площині в просторі.

1. Нехай дано два ненульові колініарні вектори ,. Тоді існує числотаке, що

Дійсно, можна знайти як відношення. Якщо векториоднаково напрямлені,, то числобуде додатним,>0, і якщо , то<0.

2. Нехай на площині задані два неколініарні вектори , , і вектор, що належить цій же площині. Знайти розклад вектораза напрямками векторів(рис. 10).

Рис. 10

Побудуємо паралелограм ОВАС, діагональ якого вектор , а сторони ОВ і ОС розміщені на напрямках векторів. Тоді

Але , тоді за аналогією з (1) існує числотаке, що. Так само.

Отже,

Коефіцієнти розкладу називаються координатами векторав системі векторів.

3. Нехай в просторі задано три некомпланарні вектори зведені до спільної точки О і вектор. Тоді має місце розклад:

де - деякі числа, називаються координатами векторав системі векторов(рис. 11).

Рис. 11

Для доведення (3) проведемо з точки А (кінець вектора ) прямудо перетину з площиною векторівв точці М. Далі, проведемо до перетину з напрямком в точці. ОМАD - паралелограм. Для вектора маємо

.

Вектор компланарний з, тому згідно (2) існують числатакі, що

Крім того, , тому за аналогією з (1) існує числотаке, що. Остаточно отримуємо рівність (3).

2.3. Лінійна залежність і лінійна незалежність системи векторів

Означення 1. Система векторів називаєтьсялінійно залежною, якщо їх лінійна комбінація дорівнює нульовому вектору:

за умови, що хоча б один з коефіцієнтів відмінний від нуля.

Якщо система векторів лінійно залежна, то хоча б один з них можна подати у вигляді лінійної комбінації інших. Дійсно, якщо, наприклад, , то з (1) випливає:

;

Навпаки, якщо лінійна комбінація векторів, тобто

,

то вся система - лінійно залежна, бо

де .

Означення 2. Система векторів називаєтьсялінійно незалежною, якщо їх лінійна комбінація дорівнює нульовому вектору:

тільки за умови рівності нулю всіх коефіцієнтів .

Поняття лінійної залежності векторів дозволяє характеризувати їх взаємне положення в просторі.

Теорема 1. Два вектори лінійно залежні тоді і тільки тоді, коли вони колінеарні.

Теорема 2. Довільні три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні.

Теорема 3. Чотири вектори завжди лінійно залежні, тобто існують числа такі, що для векторівмає місце співвідношення:

Зауваження. Розклад (2) за системою трьох некомпланарних векторів - єдиний.

Дійсно, якщо припустити, що існує ще один розклад:

то віднімаючи із (2) останню рівність, отримаємо:

Оскільки - лінійно незалежні (вони не компланарні), то це можливо за умови

Приклад. Накресліть довільний базис Побудуйте вектори,,і