Матричные игры

Парную игру с нулевой суммой удобно исследовать, если она описана в виде так называемой платежной матрицы (таблица 1). Такую игру называют матричной.

В парной игре с ненулевой суммой выигрыш каждого игрока задается своей платежной матрицей. Поэтому такие игры называют биматричными.

Рассмотрим игру, в которой участвуют два игрока, причем каждый из них имеет конечное число стратегий.

Обозначим для удобства одного игрока через А, а другого − через В.

Предположим, что игрок А имеет т стратегий: А₁, А₂, …, А_т, а игрок В – п стратегий: В₁, В₂, …, В_п.

Пусть игрок А выбрал стратегию А_i, а игрок В – стратегию В_k.

Будем считать, что выбор игроками стратегий А_i и В_k однозначно определяет исход игры – выигрыш а_ik и выигрыш b_ik игрока В, причем эти выигрыши связаны равенством

b_ik = - а_ik.

Последнее условие показывает, что в рассматриваемых обстоятельствах выигрыш одного из игроков равен выигрышу другого, взятому с противоположным знаком. Поэтому при анализе такой игры можно рассматривать выигрыши только одного из игроков. Пусть это будут, например, выигрыши игрока А.

Если нам известны значения а_ik выигрыша при каждой паре стратегий (в каждой ситуации) {А_i, В_k} , то их удобно записывать в виде прямоугольной таблицы, строки которой соответствуют стратегиям игрокаА, а столбцы – игрока В,

Таблица 1

Вk Аi,	В1	В2	…	Вп
А1	а11	а12	…	а1п
А2	а21	а22	…	а2п
…	…	…	…	…
Ат	ат1	ат2	…	атп

или матрицы

Полученная матрица имеет размер т × п и называется матрицей игры или платежной матрицей.

Рассматриваемую игру часто называют игрой т × п или т × п-игрой.

Матричные игры относятся к разряду антагонистических игр.

Пример 1. Каждый из двух игроков А и В одновременно и независимо друг от друга записывают на листе бумаги любое целое число. Если записанные числа имеют одинаковую четность, то игрок А получает от игрока В 10 рублей, а если разную, то, наоборот, игрок А платит 10 рублей игроку В.

У игрока А две стратегии: А₁ – записать четное число и А₂ – записать нечетное число.

У игрока В также две стратегии: В₁ − записать четное число и В₂ – записать нечетное число.

Выбор игроками соответственно стратегий А_i и В_k однозначно определяет исход игры: а_ik – выигрыш игрока А.

Матрица этой 2×2-игры имеет следующий вид:

.

Строки этой матрицы соответствуют стратегиям игрока А, а столбцы – стратегиям игрока В.

Лекция 2

Ситуация равновесия в матричной игре

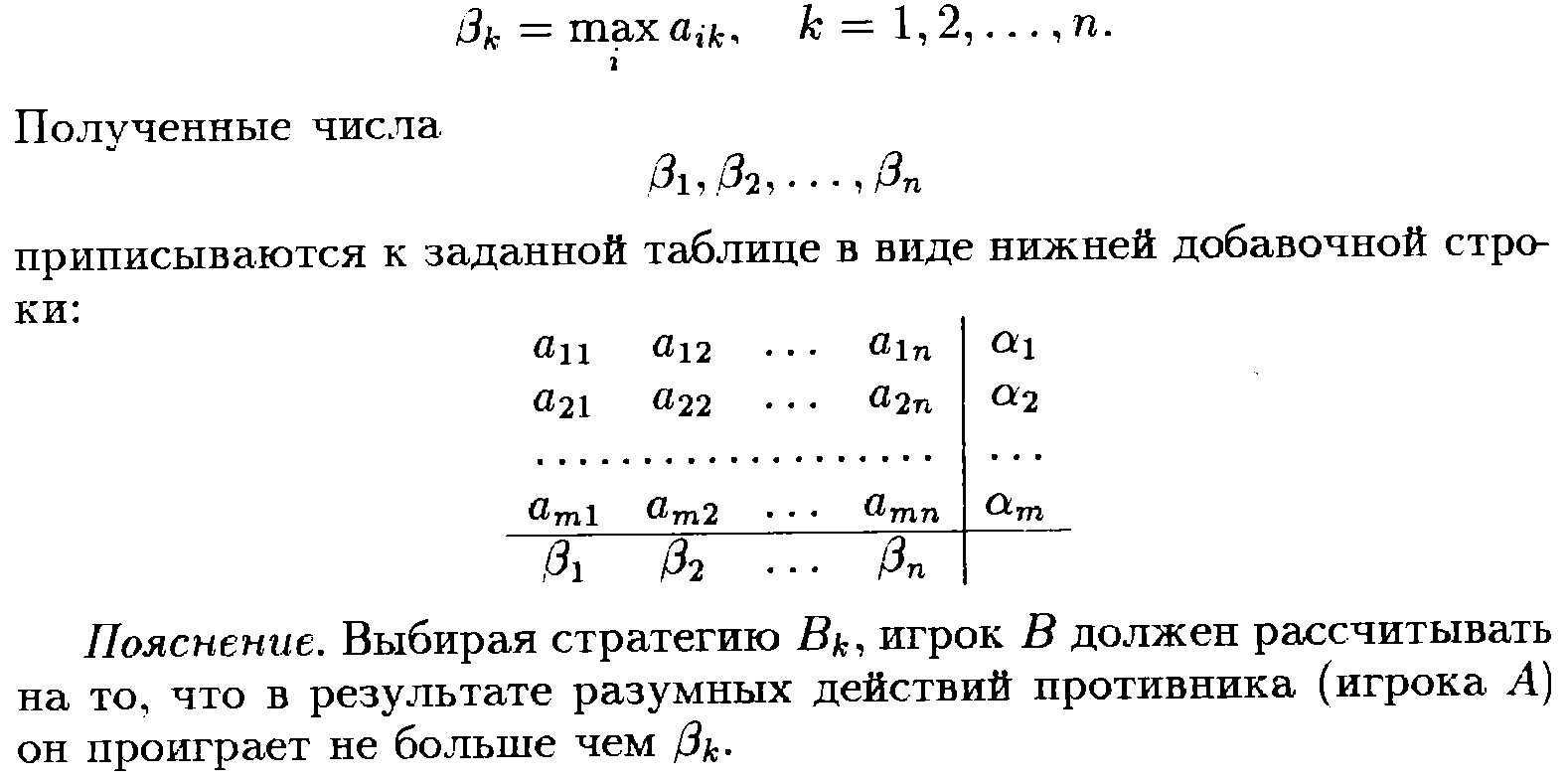
Лекция 3

Смешанные стратегии матричной игры

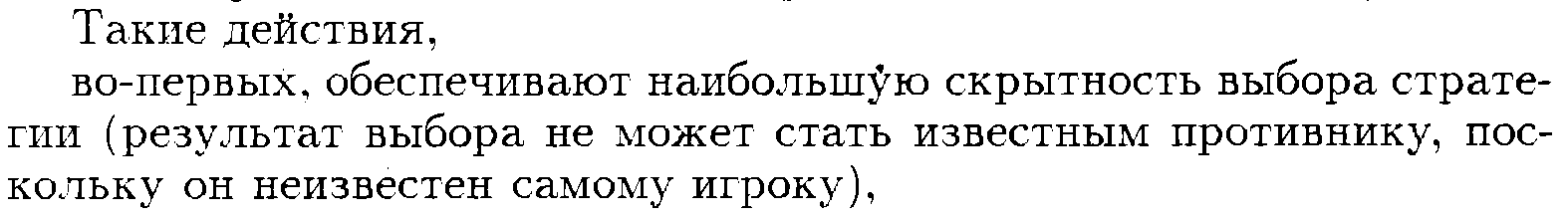
Лекция 4

Графический способ решения 2n-игр

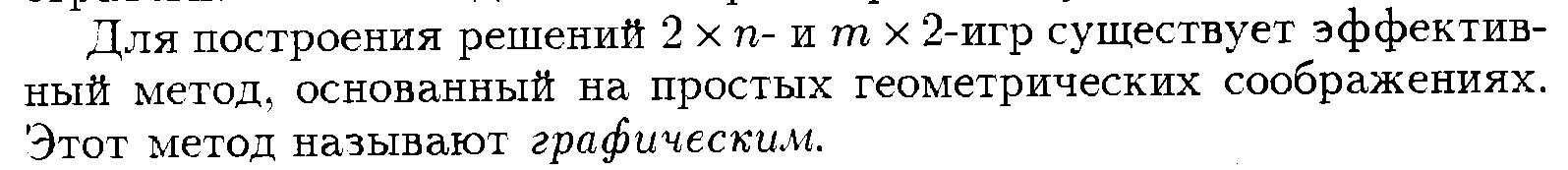
Лекция 5

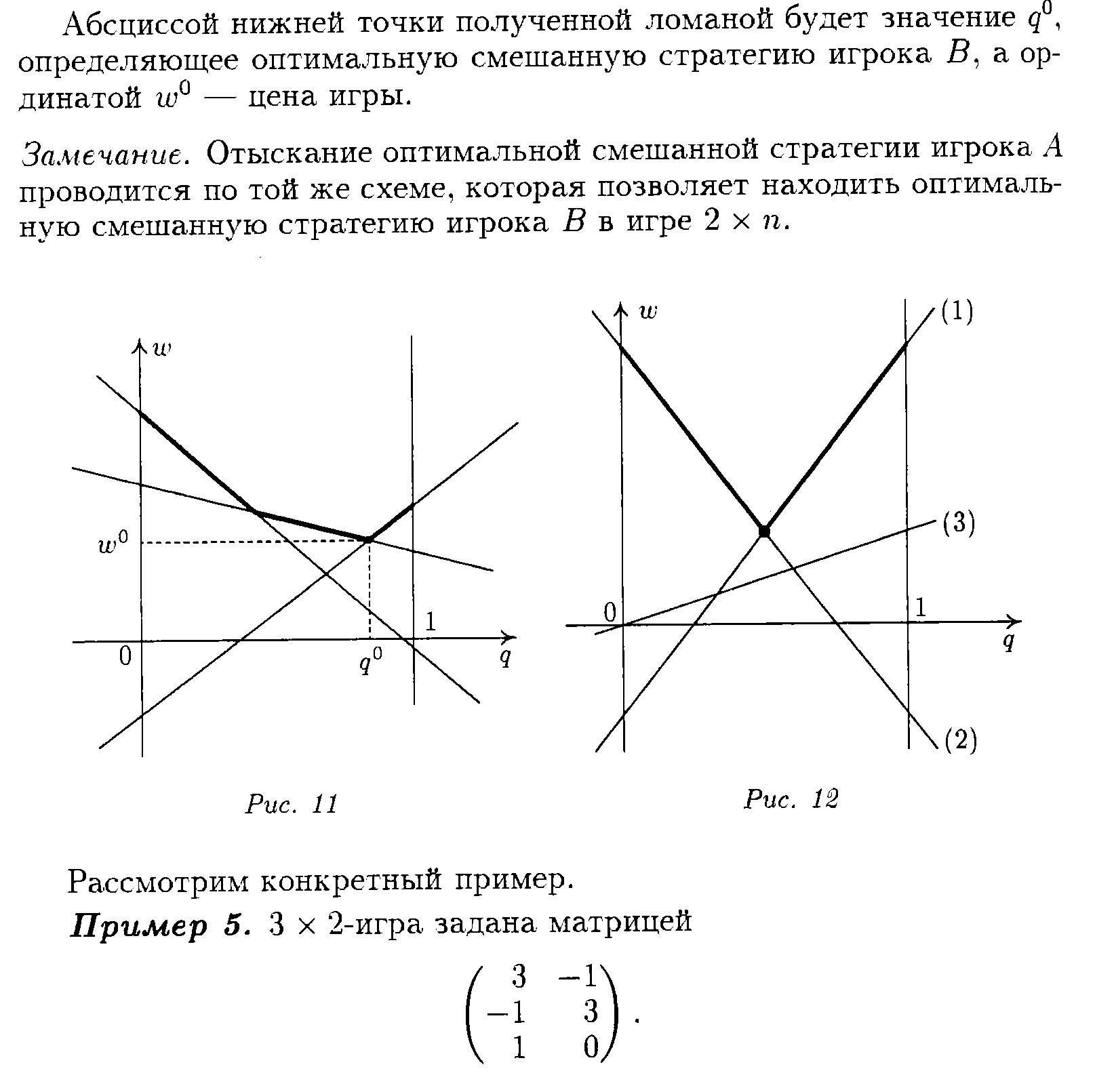
Решение m2-игры. Игры с произвольной платежной матрицей

Лекция 6

Итерационный метод решения матричных игр

Лекция 7

6.3. Сведение матричной игры к задаче линейного программирования

При решении матричной игры в смешанных стратегиях можно использовать метод сведения игры к задаче линейного программирования.

Пусть игра задана платёжной матрицей . Тогда оптимальные смешанные стратегии игроковА и В могут быть найдены в результате решения пары взаимодвойственных задач линейного программирования.

Задача 1. (для игрока А)

В результате решения задачи 1 находят её оптимальный план и значение задачи. Затем определяют цену игры v и компоненты смешанной стратегии по формулам

.

Задача 2. (для игрока В)

Пусть – оптимальный план задачи 2 и− её значение. Тогда цена игрыv и компоненты смешанной стратегии определяются равенствами

.

Поскольку задачи 1 и 2 образуют пару симметрических взаимодвойственных задач, то, решив одну из них, можно найти решение другой, воспользовавшись соответствием между переменными в канонических записях задач.

Пример 6.6. Предприятие может выпускать три вида продукции (А₁, А₂, А₃), получая при этом прибыль, зависящую от спроса. Спрос, в свою очередь, может принимать одно из четырёх состояний П₁, П₂, П₃ и П₄. Прибыль, которую получит предприятие при выпуске продукции А_i и состоянии П_j (), составитu_ij ден. ед.

Предполагая состояние спроса полностью неопределённым, определить оптимальные пропорции в выпускаемой продукции, гарантируя при этом среднюю величину прибыли при любом состоянии спроса.

Числовые данные задачи представлены матрицей :

.

Решение. Используя игровой подход, примем за игрока А – руководство предприятия, принимающее решение о пропорциях в выпуске продукции трёх видов. Чистыми стратегиями игрока являются стратегии А_i – выпуск продукции только одного вида А_i (). Совокупность обстоятельств, формирующих спрос на продукцию, примем за второго игрока – природуП. Согласно условию природа может реализовать одно из своих состояний П₁, П₂, П₃ и П₄.

Итак, задача имеет характер статистической игры. Элементы а_ij платёжной матрицы характеризуют прибыль предприятия при различных комбинациях (А_i,П_j) ().

Таблица 68

Пj	П1	П2	П3	П4
Ai
A1	6	6	4	2	2
А2	4	5	2	8	2
A3	3	4	6	3	3
	6	6	6	8

Доминируемых строк платёжная матрица не имеет. Доминируемые столбцы (при их наличии) матрицы статистической игры не исключаются, так как природа может реализовать любое из своих состояний. Таким образом, упрощение платёжной матрицы невозможно.

Гарантируемая средняя величина прибыли предприятия (игрока А) будет обеспечена при выборе им максиминной стратегии.

Находим нижнюю и верхнюю чистые цены игры:

Так как , то игра не имеет решения в чистых стратегиях. Найдём её решение в смешанных стратегиях.

Составим задачу линейного программирования для отыскания оптимальной стратегии игрокаА:

(6.1)

Представим эту задачу в канонической форме

(6.2)

Двойственная к этой задаче имеет вид:

(6.3)

Установим следующее взаимооднозначное соответствие между переменными задач (6.2) и (6.3)

Решим задачу (6.3) симплексным методом. Исходная симплексная таблица имеет вид:

Таблица 69

СП					bi
БП
y5	6	6	4	2	1
y6	4	5	2	8	1
y7	3	4	6	3	1
g	–1	–1	–1	–1	0

В качестве разрешающего столбца в таблице 69 примем третий столбец. По минимальному симплексному отношению определяем разрешающим элементом число 6 в разрешающем столбце. С помощью симплексных преобразований переходим к таблице 70.

Таблица 70

СП БП					bi
y5	4			0
y6	3			7
y3
g

Полученный в таблице 70 опорный план не является оптимальным. Переходим к другому.

В качестве разрешающего выбираем первый столбец, а в качестве разрешающего элемента в нём число 4. После симплексных преобразований получим таблицу 71.

Таблица 71

СП БП					bi
y1				0
y6				7
y3
g

Так как представленный в таблице 71опорный план также не является оптимальным, то переходим к новому опорному плану. После симплексных преобразований получим таблицу 72.

Таблица 72

СП БП					bi
y1				0
y6
y3
g

Так как в последней строке таблицы 72 нет отрицательных чисел, то представленный в ней опорный план является оптимальным планом задачи. Запишем его:

Используя соответствие между переменными задачи 2.2 и 2.3 по симплексной таблице 2.4, находим оптимальный план задачи 9.2:

При этом . Цена игры.

Находим компоненты оптимальной смешанной стратегии игрокаА.

Полученное решение означает, что средняя величина прибыли при любом состоянии спроса будет гарантирована, если в общем объёме продукции, выпускаемой предприятием, продукция вида А₁ составит 30%, А₂ – 30% и А₃ – 40%.